基于一种遗传算法的最小测试用例集自动生成

刘 冬，靳蓓蓓，阙向红

(1.皖南医学院第一附属医院 计算机中心，安徽 芜湖 241001；2.华中科技大学 网络与计算中心，湖北 武汉 430030；3.安徽师范大学，安徽 芜湖 241000)

基于一种遗传算法的最小测试用例集自动生成

刘 冬1,2，靳蓓蓓3，阙向红2

(1.皖南医学院第一附属医院 计算机中心，安徽 芜湖 241001；2.华中科技大学 网络与计算中心，湖北 武汉 430030；3.安徽师范大学，安徽 芜湖 241000)

测试数据的生成是一个复杂的问题，且其技术和方法还不成熟。在生成最小测试用例集过程中，为了避免基本遗传算法对已经满足测试需求的测试用例重复进行遗传操作，文中在基本遗传算法的基础上，最大提高遗传算法的稳定性，提出最大稳定遗传算法(LSGA)。该算法能很好地保证种群的最大稳定性，提高搜索性能，最后对该算法从概率角度理论证明其优越性。实例分析表明，利用该算法能较快生成最小测试用例集，从而实现对测试目标的充分测试，提高测试效率，降低测试成本。

测试用例集;测试用例;基本路径集;基本遗传算法;软件测试

1 概 述

自动生成测试用例的问题是一个非常困难的问题，也是软件测试自动化的一个重要环节。自从基本遗传算法被提出，许多研究者在软件测试中不断尝试引入基本遗传算法。Jones[1]和Hermadi[2]引入基本遗传算法(GA)解决自动生成测试用例问题，并进行性能分析。文献[3]比较了GA和梯度下降法的搜索性能，并通过两个具体的实例验证了GA明显优于梯度下降法。Jones[4]和Wegener[5]的研究证明，通过GA生成的测试用例数明显少于梯度下降法。然而之前的研究成果都是根据给出的某一个测试需求，使用各类算法生成测试用例，该用例满足这个测试需求。例如文献[6]中阐述的基于路径的自动生成测试数据，为实现路径覆盖，用模拟退火遗传算法或其他启发式算法测试人工选择的一条路径，从而产生一个测试用例，覆盖该路径，而想要覆盖其他不同的路径，就必须由人工不停选择不同的测试路径。这样就暴露出一个问题。若测试需要待测程序中所有路径都被覆盖，就必须人工指定所有测试路径。那么工作量就比较大，费时、费力。

因此，文中希望能自动生成一个最小测试用例集，该用例集中的测试用例能全部覆盖所有路径，且每个测试用例仅覆盖其中一条路径。有关生成最小测试用例集的问题已经有大量的研究成果。

Johnson[7]引入贪心算法对测试用例集进行精简。文献[8]提出一种根据测试用例的重要性来选择用例的启发式方法，并用该方法实现冗余测试用例的删减。在结合了贪心算法和启发式算法优点的基础上，Chen和Lau[9-10]提出了一种新的测试用例集简化的启发式算法。此外，Lee和Chung[11]将简化测试用例集问题转化成整数规划问题，并把整数规划方法用于选择测试用例，该方法可以保证选出的测试用例组成的用例集是最优的简化测试用例集。文献[12]充分考虑测试目标中测试需求之间的相互关系，划分所有满足测试需求的可用测试用例，从而形成一个测试用例集，然后再运用上述算法进行简化。马雪英[13]和全君林[14]分别研究了遗传算法在测试用例集最小化中的应用。申利民等[15]提出一种基于遗传蚁群融合算法的测试用例最小化方法。

为了实现最小测试用例集的自动生成，文中用一个测试用例满足基本路径集中的一个独立路径，通过独立路径表记录测试需求满足情况，给出最大稳定遗传算法(LSGA)[16]，并从概率角度理论证明其比基本遗传算法优越。最后通过实例分析表明，该算法比基本遗传算法具有更高的效率。

2 LSGA算法

2.1 算法描述

第2步：将获得的种群运行待测程序。

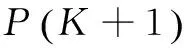
第7步：检验停止标准，若满足则停止，否则K=K+1，并返回第2步。

2.2 构造适应度函数

在实际问题的应用过程中，适应度函数是LSGA算法和实际问题的接口，利用其评价最优解。文中为了获得最小测试用例集并且覆盖待测程序中的所有路径，记录已经覆盖过的路径，采用“邻近者优先”的原则，再动态修正其适应度值。具体算法实现如下：

第1步：初始化初始种群中每个个体的适应度，一般为所要覆盖的路径数Cmax。

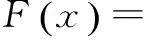
第4步：判断是否覆盖了待测程序的所有路径，是则结束，否则进入下一代操作，重复第2步。

2.3 算法性能分析

与GA算法相比，LSGA算法具有较强的效率。下面从概率角度对它的优越性进行描述和证明。

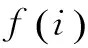
引理1：K代种群中，个体i满足某个测试需求的概率：

证明：因为二进制个体串长为L，所以个体串最多有2L种位串。考虑种群规模M与2L-1之间的关系，可以分为三种关系：M>2L-1，M=2L-1和M<2L-1。对于这三种关系，某代种群中可能含有多个相同的个体，即Z(i,k)>1，对于前两种关系可能存在Z(i,k)=0，在第三种关系中一定存在Z(i,k)=0的情况。为了使Z(i,k)无论取什么值都不影响统计种群中个体i满足某个测试需求的概率，这里使用加权概率统计法。

其中权值为个体i的适应度值，可以表示为：

证毕。

引理1给出了评价个体满足测试需求的概率公式，由此下面就可以利用该公式证明LSGA算法的优越性。

定理1：个体i利用LSGA算法生成最小测试用例集的概率比GA算法大。

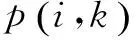
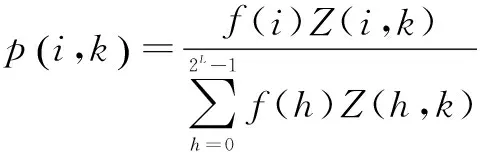
证毕。

定理2：LSGA算法能以概率满足终止条件的迭代代数少于GA算法。

证明：根据轮盘赌选择法计算概率可得到LSGA算法第K代终止的概率为：

GA算法第K代终止的概率为：

证毕。

3 实例分析

前面已经从概率角度理论证明了LSGA算法比GA算法优越，该算法仍然是启发式方法，算法的有效性应该通过实验来验证。本节通过软件测试中常见的一个测试案例—直角三角形判定程序来验证LSGA算法的优越性。

在研究过程中，笔者开发了最小测试用例集自动生成的系统原型。系统通过分别调用LSGA算法包和GA算法包，分别记录两种算法生成最小测试用例集的迭代代数。由于初始种群是随机生成的，为了保证数据的可信性，这里针对每个实验分别执行10次，然后取其平均值。

3.1 实验验证

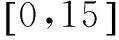
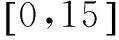
3.2 实验结果

对LSGA算法和GA算法得到最小测试用例集的运行时间进行了考察，结果如图1、图2所示。

从图中可以很清晰地看出，利用LSGA算法生成最小测试用例集的运行时间远小于用GA算法生成最小测试用例集的运行时间，具有很好的效益。

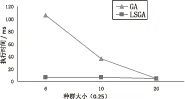
图1 实验1运行时间对比图

图2 实验2运行时间对比图

4 结束语

文中对LSGA算法进行了理论分析，该算法能很好地保证种群的最大稳定性，提高搜索性能。首先从概率角度理论证明了LSGA算法优越于GA算法，然后将算法用于实例验证。结果表明，利用该算法能较快生成最小测试用例集，从而实现对测试目标的充分测试，提高测试效率，降低测试成本。

[1] Jones B F,Sthamer H H,Eyres D E.Automatic structural testing using genetic algorithms[J].Software Engineering Journal,1996,11(5):299-306.

[2] Hermadi I, Ahmed M A. Genetic algorithm based test data generator[C]//Proc of 2003 congress on evolutionary computation.[s.l.]:[s.n.],2003:85-91.

[3] Michael C C,McGraw G E,Schatz M A,et al.Genetic algorithms for dynamic test data generation[C]//Proc of 12th IEEE international conference on automated software engi-

neering.[s.l.]:IEEE,1997:307-308.

[4] Jones B F,Eyres D E,Sthamer H H.A strategy for using genetic algorithms to automate branch and fault-based testing[J].The Computer Journal,1998,41(2):98-107.

[5] Wegener J,Baresel A,Sthamer H.Evolutionary test environment for automatic structural testing[J].Information and Software Technology,2001,43(4):841-854.

[6] Eugenia D,Javier T,Raquel B.Automated software testing using a metaheuristic technique based on tabu search[C]//Proc of 18th IEEE international conference on automated software engineering.[s.l.]:IEEE,2003:310-313.

[7] Johnson D S.Approximation algorithms for combinatorial problems[J].Journal of Computer and System Sciences,1974,9(3):256-278.

[8] Harrold M J,Gupta R,Soffa M L.A methodology for controlling the size of a test suite[J].ACM Transactions on Software Engineering and Methodology,1993,2(3):270-285.

[9] Chen T Y,Lau M F.A new heuristic for test suite reduction[J].Information and Software Technology,1998,40(5-6):347-354.

[10] Chen T Y,Lau M F.Heuristics towards the optimization of the size of a test suite[C]//Proceedings of the 3rd international conference on software quality management.Seville,Espagne:[s.n.],1995:415-424.

[11] Lee J G,Chung C G.An optimal representative set selection method[J].Information and Software Technology,2000,42(1):17-25.

[12] 聂长海,徐宝文.一种最小测试用例集生成方法[J].计算机学报,2003,26(12):1690-1695.

[13] 马雪英,盛斌奎,叶澄清.用遗传算法的测试用例最小化[J].计算机科学,2007,34(1):285-288.

[14] 全君林,陆 璐.基于遗传算法测试用例集极小化研究[J].计算机工程与应用,2009,45(19):58-61.

[15] 申利民,高 洁.基于遗传蚁群融合算法的测试用例最小化研究[J].计算机工程,2012,38(16):57-60.

[16] 刘 冬,靳蓓蓓,阙向红.基于LSGA的最小测试用例集自动生成[J].微电子学与计算机,2011,28(12):115-118.

Automatic Generation of Minimal Test Set Based on a Genetic Algorithm

LIU Dong1,2,JIN Bei-bei3,QUE Xiang-hong2

(1.Computing Center,First Affiliated Hospital of Wannan Medical College,Wuhu 241001,China; 2.Computing Center,Huazhong University of Science and Technology,Wuhan 430030,China; 3.Anhui Normal University,Wuhu 241000,China)

Test data generation is a complicated problem and its method and technique is not mature.In the process of the minimum test case generation,the Largest Steady Genetic Algorithm (LSGA) is proposed to improve the stability greatly,which is based on the basic genetic algorithm,in order to avoid repeat genetic manipulation of test case which has been met the testing requirement.This algorithm can guarantee the largest population stability and improve the search performance.Contrasted with the genetic algorithm,its superiority is proved from the perspective of the probability.Example analysis shows that using the proposed algorithm can rapidly generate minimum test case sets,achieving the target of the full test,improving the test efficiency and reducing test cost.

test set;test case;basic path set;simple genetic algorithm;software testing

2015-04-16

2015-08-18

时间：2016-03-22

国家自然科学基金专项基金项目(81141073);安徽省科技计划项目(1301042203);安徽省高校省级自然科学研究重点项目(KJ2015A241);芜湖市科技计划项目(2012hm35-1)

刘 冬(1979-),男,硕士,高级工程师,研究方向为软件测试、医学信息处理等。

http://www.cnki.net/kcms/detail/61.1450.TP.20160322.1518.026.html

TP301.6

A

1673-629X(2016)04-0086-04

10.3969/j.issn.1673-629X.2016.04.019