贝叶斯决策树方法在招生数据挖掘中的应用

黄春华，陈忠伟，李石君

(1.武汉大学 计算机学院，湖北 武汉 430072；2.广西英华国际职业学院 工信学院，广西 钦州 535000)

贝叶斯决策树方法在招生数据挖掘中的应用

黄春华1,2，陈忠伟2，李石君1

(1.武汉大学 计算机学院，湖北 武汉 430072；2.广西英华国际职业学院 工信学院，广西 钦州 535000)

文中首先简单介绍了贝叶斯决策树方法的基本思想，该方法结合了贝叶斯分类的先验信息方法和决策树分类的信息增益方法的优点，加入贝叶斯节点弥补了决策树不能处理具有二义性或存在缺失值数据的缺点。在此基础上，文中设计了一种基于朴素贝叶斯方法和ID3算法的贝叶斯决策树算法——NBDT-ID3算法，并给出了该算法的设计及分析过程。然后将该算法应用到高职招生数据挖掘中，对新生报到情况进行分析与预测，并在Matlab环境下进行了实验验证。实验结果表明，NBDT-ID3算法在付出一定时间代价的情况下，不仅可以获得更高的分类精度，而且在处理二义性、不完整或不一致数据方面具有更好的效果。

数据挖掘；贝叶斯决策树；分类；招生数据；报到预测

招生工作一直是民办高职院校工作的重中之重，因为生源是其生存之本。如何有针对性地开展招生工作，既能提高新生的报到率又能节省招生成本，一直是民办高职院校非常关心的问题之一。数据挖掘技术是通过分析大量不完整的、模糊的、随机的数据来发现隐藏的、潜在有用的知识和规则的过程[1]。学校可以通过结合数据挖掘技术和招生工作经验，对历年招生数据进行分析，从中寻找到有价值的信息，以此指导学校制定合理的招生计划，将有限的人力物力用在能“产出”大量生源的地方，提高新生报到率，达到招生效益最大化。

目前用于招生数据挖掘的方法有关联规则、决策树分类、支持向量机等[2-3]，但是每一类方法都有一定的应用局限性。决策树分类算法是以实例为基础的归纳学习算法，通过信息增益来构建决策树，只需要在训练和测试这两个阶段进行简单的比较，对数据类别的要求不高，计算过程简单，主要着眼于从一组给定的无次序、无规则样本数据中推理出以决策树表示的分类规则，结果表现直观[4]。但是该类算法的主要缺点是对缺失或二义性数据难以产生正确的分支，以致影响整个决策树的生成，从而降低了分类的准确性[4]。针对这个不足之处，可以将贝叶斯分类方法引入决策树学习模型中，前者具有坚实的数学基础且算法具有简单直观、易实现、时空开销小、健壮性小等优点[5]。这样不仅可以更好地处理包含不一致性或不完整等非规律性数据的集合，还可以将先验知识与概率背景融入决策树分类模型中[6]。

目前基于贝叶斯决策树的数据挖掘算法已经得到许多学者的研究并被应用到不同的领域中。尹婷等[7]将基于贝叶斯决策树的方法应用到电信企业客户流失分析与预测中；徐哲等[8]将贝叶斯决策树方法应用到识别英文现在分词的词性中；王琦[9]构建了一种基于贝叶斯决策树算法的垃圾邮件识别机制。

在简单介绍了贝叶斯决策树方法基本思想的基础之上，文中详细给出了一种基于朴素贝叶斯方法和ID3算法的贝叶斯决策树分类算法，并根据民办高职院校招生工作及其数据特点，将该算法应用到高职招生数据挖掘中，主要对新生报到情况的分析与预测进行了初步研究。

1 贝叶斯决策树方法

1.1 贝叶斯分类方法

贝叶斯分类方法基于贝叶斯定理，其关键在于使用概率表示各种形式的不确定性，即通过变换事件的先验概率及后验概率，配合决定分类特性的各属性彼此间是相互独立的假设来预测分类的结果[10]。下面以朴素贝叶斯(Naïve Bayesian)分类方法为例，给出一个贝叶斯分类方法的工作过程[11-12]。

(1)设D是训练元组和它们相关联的类标号的集合，通常每个元组用一个k维属性向量X=(x1,x2,…,xk)表示，描述由k个属性A1,A2,…,Ak对元组的k个测量。

(2)假定有l个类别C1,C2,…,Cl，给定元组X，分类法将预测X属于具有最高后验概率的类别(在条件X下)。根据贝叶斯定理的公式可得：

(1)

其中：p(Ci)是先验概率；p(Ci|X)是后验概率。

由此可知，朴素贝叶斯分类法预测X属于类别Ci当且仅当p(Ci|X)>p(Cj|X)，其中1≤j≤l，且i≠j。

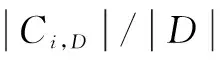
(4)当给定的数据集中具有许多属性时，计算p(X|Ci)的开销可能会很大，可以通过做类条件独立的朴素假定来降低计算开销。因此有：

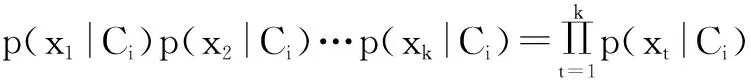
(2)

(5)为了预测X的类别标号，对每个类别Ci，计算p(X|Ci)p(Ci)。则朴素贝叶斯分类法预测X属于类别Ci可最终表述为当且仅当p(X|Ci)p(Ci)>p(X|Cj)p(Cj)，其中1≤j≤l，i≠j。根据式(2)可进一步得到：

(3)

即被预测的类别标号是使p(X|Ci)p(Ci)最大的类Ci。

1.2 决策树

决策树(Decision Tree)又称为判定树，是一种以树状结构形式来表达的预测分析模型，是数据挖掘技术中一种重要的分类方法。根据给定的一个类标号未知的实例，可以在决策树上测试该实例的属性值，并跟踪一条由根到叶子节点的路径，则该叶子节点就存放着该实例的类预测。决策树的主要优点是描述简单，分类速度快，特别适合大规模的数据处理[4]。图1是一棵决策树。

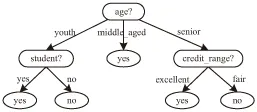
图1 决策树举例

1.3 贝叶斯决策树方法简介

定义：在原有决策树的两个属性测试节点之间加入一个能够根据贝叶斯原理进行函数计算[13]的新节点，该节点即是贝叶斯节点(Bayesian Node,BN)。相应地将具有贝叶斯节点的决策树称为贝叶斯决策树(Bayesian Decision Tree,BDT)，其结构如图2所示。

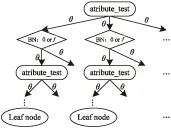
图2 BDT的结构

由图2可知，BN包含两个值：0和f。当BN取值为0时，该节点只需根据属性测试条件θ直接转向下一个属性测试节点，不必进行任何计算；当BN取值为f时，该节点需要计算函数f的值，并根据属性测试条件θ转向下一个属性测试节点，即当BN取值为f时，下一个属性节点的选择依赖于两点：函数f的值和属性测试条件θ。这里的函数f根据具体情况可以是朴素贝叶斯公式也可以是其他贝叶斯公式。

需要说明的一点是，当根据函数f和属性测试条件θ进行下一属性节点的选择时，都采用IF……THEN……的表达形式进行描述[6]。

2 算法的设计及分析

2.1 算法设计思路

根据贝叶斯决策树分类算法的基本思想，以下给出一种基于朴素贝叶斯方法和ID3算法的贝叶斯决策树分类算法(NBDT-ID3)的设计思路：

(1)当使用决策树的信息增益方法就可确定选择某个属性的分支时，BN的取值为0。其中ID3算法信息增益的计算方法[11]如下所述：

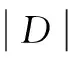
(4)

假设要按某个属性A划分D中的元组，其中属性A根据训练数据的观测值具有v个不同值{a1,a2,…,av}。可以用属性A将D划分为v个子集{D1,D2,…,Dv}，其中Dj(j=1,2,…,v)包含D中的元组，它们对应于属性A的值为aj。如果A作为测试属性，那么这些子集对应于由D的节点生长出来的分枝。基于按属性A划分对D的元组分类所需要的期望信息为：

(5)

信息增益定义为原来的信息需求(仅基于类比例)与新的信息需求(对A划分后)之间的差值，即：

Gain(A)=Info(D)-InfoA(D)

(6)

(2)当数据分类具有二义性，即数据对象的分类类别无法确定或属性值丢失时，BN的取值为f。这里的f选择为朴素贝叶斯公式，即根据以前的经验知识或实验结果得出该数据对象的先验概率值，再以此值来判断可以先将其分到某些类中，然后运用贝叶斯分类方法确定这些类的后验概率值，最后选择后验概率值最大的那一类作为该数据对象的所属类别[6]。

2.2 算法流程

根据以上设计思路，给出NBDT-ID3算法流程：

输入：数据集{X1,X2,…,Xn}，其中每个数据Xi具有m个属性xij(i=1,2,…,n;j=1,2,…,m);

输出：显示或打印出对数据集{X1,X2,…,Xn}已划分到各个相关类别Ck(k=1,2,…)中的数据。

(1)根据事先给定的类别特征或属性确定要生成的类别集合{C1,C2,…,Cl}，并确定类别数目l。

(2)运用2.1节中信息增益的计算方法先确定优先判断的属性，然后确定要进行分类的数据Xi(i=1,2,…)的某个或某些属性，属性值与相应的类别相关。

(3)当属性选择和数据分类都无二义性时，BN的取值为0，直接根据属性测试条件转向下一个属性测试，转到(2)，否则转到(4)。

(4)对Xi进行分类。若Xi确定对应某一类别Ck，则将Xi划分到该类别中；若Xi不能确定划分到哪一个类别中，而是与某些类别都可能相关，则根据1.1中所述的朴素贝叶斯分类方法计算出最大的p(Xi|Ck)p(Ck)值，并将Xi划分到相应类别中。

(5)BN的取值为f，且f=max(p(Xi|Ck)p(Ck))，转到(3)。

2.3 算法分析

NBDT-ID3算法仍然具有与决策树分类算法的产生规则易于理解、分类速度相对较快等相似的优点[6]。该算法主要包括两项工作：判断是否要计算f值和判断是否要计算属性的后验概率值。根据上述的算法流程，最坏的情况就是需要计算所有数据的后验概率值。假设共有n个数据待分类，且每个数据有m个属性，需要把它们划分到k个类别中，计算一个数据的后验概率值需要时间t1，计算信息增益值需要时间t2，此时算法的计算时间为：

(t1+mt2)·n·k=nkt1+nmt2

(7)

当m=n=k时，计算时间为n2t1+n3t2，则此时算法的时间复杂度为O(n3)。

NBDT-ID3算法自身具有的优点如下：

(1)具有更高的分类精度和准确率。分类一般按照数据的某个或某些属性进行，假如根据数据集计算出来的两个不同属性的信息增益值相等，则属性的选择出现了二义性。大量的数据二义性必然会对数据集的分类精度和准确率产生不良影响。而NBDT-ID3算法通过引入朴素贝叶斯方法，可很好地利用先验信息去处理这些数据二义性，提高分类的精度和准确率。

(2)具有更强的分类鲁棒性。数据挖掘一般处理的都是海量数据，这些数据由于主客观原因难免会存在大量不完整、不一致和噪声等干扰数据。可以通过预处理的方法[11]对这些干扰数据进行处理，但该解决方法一般较为耗时耗力。NBDT-ID3算法通过运用朴素贝叶斯方法，可以根据历史数据的先验信息或经验来消除不一致的数据，平滑不完整的数据，排除噪声数据等[6]，相对而言省时省力，且具有更好的处理效果，从而增强了数据分类的鲁棒性。

3 NBDT-ID3算法的应用

3.1 数据准备及预处理

因为该学院的新生来源主要分为高考统招生和三校生两类，其中三校生通过中职对口的招生方式进行录取，招生来源一般是定向的，因此只对高考统招生的数据进行挖掘分析。实验数据来源于该学院2012-2014年实际的高考统招生信息。

因为不同年份招生数据表的格式有所差异，存在着相同含义的属性用不同字段名称表示的情况。比如在2012年数据表中用“入学成绩”表示高考成绩，在2013年数据表中则用“总分”表示高考成绩。为了保证数据挖掘的有效性，必须先将这些属性名称统一表示。经过初步分析，首先删除掉数据集中那些明显与数据挖掘不相关的字段，比如年份、考生姓名、身份证号、联系地址等，初步保留那些可能与招生数据挖掘相关的字段：考生号、性别、考生类别、高考成绩、报考科类、录取专业、录取专业代码和报到情况。

根据高职招生业务及其数据的特点，可以对招生数据做进一步的处理以更有利于数据挖掘工作的进行。依据全国高职高专专业目录中专业代码的含义，可以将录取专业进行泛化处理[11]；依据考生号的组成含义，可以得到每位新生的生源地区信息；采用合适的数学方法[3]对高考成绩进行离散化处理，划分出每个考生的成绩等级。最终处理得到的数据如表1所示。

3.2 算法的检验与性能评价

为了验证NBDT-ID3算法在高职新生报到预测

表1 最终处理得到的数据示例

中的应用性能，在Matlab环境下分别运用ID3决策树算法和NBDT-ID3算法对预处理后的招生数据集进行训练和测试，并对实验结果进行对比说明。预处理后的招生数据集共有2 625条新生信息记录，其中报到新生人数1 782人，未报到新生人数843人。随机抽取其中2/3的数据作为训练集建立基于贝叶斯决策树预测模型得到预测结果，再运用该模型对剩余的1/3数据进行新生报到情况的预测，然后从覆盖率和命中率两个方面对预测结果和实际结果进行对比分析。

覆盖率：实际报到预测也是报到的新生人数X占所有实际报到的新生人数的比例，它是描述模型普适性的指标[7]，用α表示，其计算公式为：

(8)

其中，Y为实际报到但预测是未报到的新生人数。

命中率：实际报到预测也是报到的新生人数X占所有预测为报到的新生人数的比例，它是描述模型精确度的指标[7]，用β表示，其计算公式为：

(9)

其中，Z为预测报到但实际并未报到新生人数。

最后得到仅应用ID3决策树算法模型与运用基于NBDT-ID3算法的贝叶斯决策树模型得到的训练结果和检验结果对比情况，见表2。

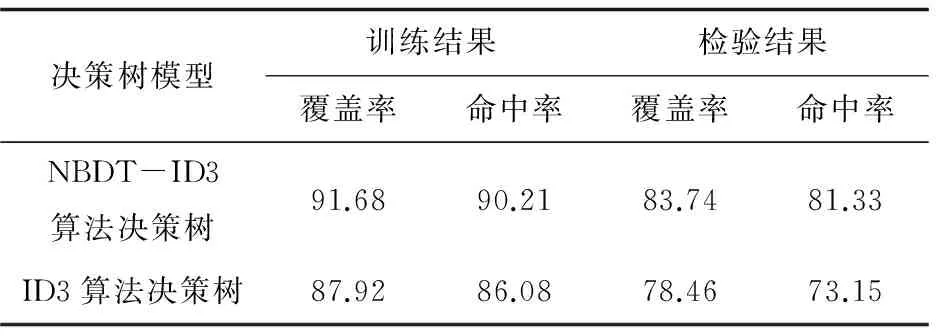
表2 两种决策树模型训练结果和

从表2的对比结果可以看出，两种决策树模型的训练结果在覆盖率和命中率上都比检验结果的好，但基于NBDT-ID3算法的决策树模型比ID3决策树算法模型无论是在训练结果还是检验结果上覆盖率和命中率都高一些，说明前者能获得较好的预测效果。

另外，建模规则和实施分类的时间也会对系统效率和性能产生影响[14]，所以有必要对算法的训练时间和分类时间进行验证和比较，以进一步评价算法的性能。同样在Matlab环境下，对NBDT-ID3算法与ID3算法在数据集训练执行过程中所需的训练时间之比和分类时间之比进行验证和比较，结果如图3所示。

图3 两种算法训练时间和分类时间对比结果

从图中可以看出，NBDT-ID3算法的训练时间和分类时间都比ID3算法的长。这是因为在构建决策树时NBDT-ID3算法需额外插入BN，在分类时NBDT-ID3算法需对选择BN值为f的节点进行后验概率计算，从而造成了额外的时间开销，但从整体上看，两者的训练时间和分类时间相差不大，时间比值保持在1.12～1.2，基本符合理想增长的趋势。

为了验证NBDT-ID3算法数据分类的鲁棒性，分别从UCI机器学习数据库Anneal、Balance-scale、Vowel中随机抽取3个数据集进行分类测试，同样在Matlab环境下运用ID3决策树和NBDT-ID3算法对数据集进行分类，比较这两种算法在建树时间之比和分类精度上的情况，结果如表3所示。

表3 两种算法数据分类的鲁棒性检验结果对比情况

从表3中可以看出，在样本缺失率较高的情况下，NBDT-ID3算法因为要计算更多选择BN值为f的节点的后验概率值,所以比ID3算法需要更长的建树时间，但在付出时间代价的情况下，NBDT-ID3算法能较好地提高分类精度。由此说明，在付出一定时间代价的情况下，NBDT-ID3算法不仅能提高分类精度，而且在处理数据不完整、不一致等缺失样本时具有更强的分类鲁棒性。

4 结束语

根据贝叶斯决策树方法的基本思想，设计了一种基于朴素贝叶斯方法和ID3算法的贝叶斯决策树分类算法——NBDT-ID3算法，并详细给出了该算法的设计及分析过程。然后将该算法应用到高职招生数据挖掘中，对新生报到情况进行预测分析。实验结果表明，NBDT-ID3算法在付出一定时间代价的情况下，可以获得更好的分类效果，并且对具有二义性、不完整或不一致的数据具有更好的处理效果。如何更加有效地将这种基于贝叶斯决策树的分类方法运用到民办高职院校招生数据的挖掘分析中，更好地为学校招生工作提供科学而直观的决策支持，是接下来需要进一步研究的工作。

[1] 朱志勇，徐长梅，刘志兵，等.基于贝叶斯网络的客户流失分析研究[J].计算机工程与科学，2013，35(3)：155-158.

[2] 孙晓莹，郭飞燕.数据挖掘在高校招生预测中的应用研究[J].计算机仿真，2012，29(4)：387-391.

[3] 詹柳春.数据挖掘技术在高校招生录取数据中的应用研究[D].广州:华南理工大学，2012.

[4]QuilanJR.Inductionofdecisiontree[J].MachineLearning,1986,1(1):81-106.

[5]Palacios-AlonsoMA,BrizuelaCA,SucarLE.EvolutionarylearningofdynamicNaïveBayesianclassifiers[J].JournalofAutomatedReasoning,2010,45(1):21-37.

[6] 樊建聪，张问银，梁永全.基于贝叶斯方法的决策树分类算法[J].计算机应用，2005，25(12)：2882-2884.

[7] 尹 婷，马 军，覃锡忠，等.贝叶斯决策树在客户流失预测中的应用[J].计算机工程与应用，2014，50(7)：125-128.

[8] 徐 哲，刘 循.贝叶斯决策树在英文现在分词词性识别中的应用[J].计算机应用，2009，29(9)：2571-2574.

[9] 王 琦.基于贝叶斯决策树算法的垃圾邮件识别机制[C]//“智慧城市和绿色IT”2011年通信与信息技术新进展——第八届中国通信学会学术年会.湖北,武汉：出版者不详，2011.

[10] 张依杨，向 阳，蒋锐权，等.朴素贝叶斯算法的MapReduce并行化分析与实现[J].计算机技术与发展，2013,23(3)：23-26.

[11]HanJiawei，KamberM，PeiJian.数据挖掘概念与技术[M].北京：机械工业出版社，2014：217-218.

[12] 黄宇达，王迤冉.基于朴素贝叶斯与ID3算法的决策树分类[J].计算机工程，2012，38(14)：41-43.

[13]FriedmanN,GeigerD,GoldszmidtM.Bayesiannetworkclassifiers[J].MachineLearning,1997,29(2-3):131-163.

[14]JingY,PavloviV,RehgJM.BoostedBayesiannetworkclassifiers[J].MachineLearning,2008,73(2):155-184.

Application of Bayesian Decision Tree Method in Admission Data Mining

HUANG Chun-hua1,2,CHEN Zhong-wei2,LI Shi-jun1

(1.School of Computer,Wuhan University,Wuhan 430072,China; 2.Dept. of Industry and Information,Guangxi Talent International College,Qinzhou 535000,China)

It simply introduces the basic thought of Bayesian decision tree method in this paper,which takes advantage of the prior information method for Bayesian classification and the information gain method of decision tree,and makes up for the decision tree cannot handle the ambiguity data and the missing value by adding Bayesian node.On this basis,a Bayesian decision tree algorithm based on Naïve Bayesian method and ID3 algorithm is presented named NBDT-ID3 algorithm.The algorithm process of the design and analysis is introduced.Then the algorithm is applied to higher vocational admission data mining,which analyzes and forecasts the new student registration.It is tested and verified under the Matlab environment.The experimental results show that NBDT-ID3 algorithm not only can get higher classification accuracy but also behave well in handling the ambiguity,incomplete or incongruous data in the case of paying certain of time.

data mining;Bayesian decision tree;classification;admission data;registration forecasting

2015-07-15

2015-10-21

时间：2016-03-22

中央高校基本科研业务费专项基金项目(2042014f0057)；湖北省自然科学基金项目(2014CFB289)

黄春华(1985-)，女，硕士，讲师，研究方向为数据挖掘、SQL数据库技术及应用。

http://www.cnki.net/kcms/detail/61.1450.TP.20160322.1521.072.html

TP301.6

A

1673-629X(2016)04-0114-05

10.3969/j.issn.1673-629X.2016.04.025