基于改进离差最大化方法的梯形灰云评估模型

范亚琼，燕雪峰，陈海燕

(南京航空航天大学 计算机科学与技术学院,江苏 南京 210016)

基于改进离差最大化方法的梯形灰云评估模型

范亚琼，燕雪峰，陈海燕

(南京航空航天大学 计算机科学与技术学院,江苏 南京 210016)

针对多方案多指标中离差最大化赋权法不能充分体现指标权重在不同方案中的差别，而层次分析法能够通过指标之间的两两比较获得指标之间的相对重要性，结合层次分析法的特性对离差最大化赋权法进行改进；同时，由于在某些领域实际监测数据所能提供的信息具有不完全性和不确知性，而云理论是一种处理模糊性和随机性信息的有效工具，结合具体应用场景，提出了基于梯形云模型的白化权函数，建立了基于改进离差最大化赋权法的梯形灰云聚类评价模型。应用梯形灰云聚类评估模型对福州市近十年的大气环境质量进行评价，实验表明该模型评价结果符合客观实际，通过灵敏度分析验证了此模型的可行性和实用性。梯形灰云聚类评价模型为综合评价问题提供了一种新的有效途径。

梯型灰云聚类；改进离差最大化赋权法；大气环境质量；灵敏度分析

0 引 言

对于现实生活中遇到的各种各样的综合评价问题，国内外综合评价方法研究人员通常采用综合指数法、层次分析法、模糊综合评价法以及灰色聚类法等对复杂问题进行评估。由于有限时空的监测数据所能提供的信息具有不完全性和非确知性，定量处理这些不明确信息的灰色聚类评价法[1]已成为研究热点。随着灰色聚类评价法的广泛应用，灰色聚类评价模型在综合评价问题中的不足也逐渐暴露出来。主要表现在：传统白化权函数仅给出了信息不完备条件下的量性转化，在许多实际情况中，信息不完备导致的灰性与随机性是共生的，某一个灰数的白化值应该是一定范围内变化的随机数，传统白化权函数对这种隶属程度的量化取值是固定的，太过僵硬。

针对上述不足，文中将梯形云[2]引入灰色聚类评价模型解决了灰性导致的随机性问题，又由于大气环境评估语表示的是某一概念，梯形云模型弥补了正态云[3]模型的不足，适用于峰值为一个区间的情况。同时，将层次分析法[4]中1～9标度法引入离差最大化赋权法[5]，弥补了离差最大化方法的不足，充分体现指标在不同方案中的重要程度。因此文中提出基于改进离差最大化赋权法的梯形灰云聚类评价模型。云聚类法[6]将表示信息模糊性和随机性的定性、定量转换的云模型引入灰色白化权函数，解决了由灰性带来的随机性问题，使得梯形灰云聚类评价模型评价结果更加精确、灵活。

1 基于层次分析法的离差最大化赋权法

传统的离差最大化赋权法通过所有方案的指标值离差之和计算指标权重，由此得到的所有方案的各指标权重是等值的，但是在动态变化的复杂系统中，这种方式显然不适合。文中结合AHP赋权法中1～9标度法改进离差最大化赋权法，根据指标值动态变化对不同方案的指标进行赋权。指标权重确定步骤如下：

Step1:构建指标值离差。在多方案多指标系统中，若第j个指标在不同方案中的指标值无差别，则该指标对不同方案的效能影响较小，应赋较小权重；反之，在不同方案中该指标值差别较大，则该指标对不同方案的效能影响较大，应赋较大权重。

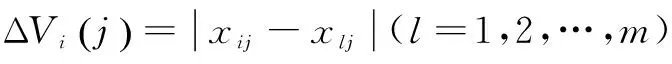
(1)

Step2:基于这种离差最大化思想，借鉴AHP赋权法，对各方案下指标间总离差进行两两对比，将结果映射到1～9标度中，进而得到相同方案下不同指标间总离差的判定矩阵B=(bij)n×n。

(2)

Step3：求解方案ti所对应判定矩阵的最大特征根λmax及其对应的特征向量wj，对其归一化：

(3)

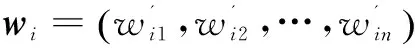
Step4:对其他方案分别执行上述操作，即可得不同方案下不同指标的权重矩阵。

(4)

2 基于改进离差最大化的梯形灰云聚类评价模型

2.1 一种梯形云模型

计算公式如下：

(5)

(6)

当实测指标数据xiCmax时，选用下降云来计算评语云模型的参数。

2.2 基于梯形云的白化函数

传统的灰云白化函数[9-10]是标准的正态云，期望值是某一个数，但是当表示某概念的定量范围不是一个值，而是一个区间时，标准正态云则不能准确描述实际情况。文中将运用梯形云[11]模型以解决期望值为一个区间的问题。

具体生成灰云及构造白化模型步骤如下：

1)确定数字特征。根据各指标的分级标准，将指标划分为g个灰类，即有g个期望区间。

(7)

(8)

(9)

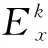
3 基于改进离差最大化赋权法的梯形灰云聚类评价模型

针对生活中多因素多层次协同作用的复杂系统评价问题，文中提出了改进离差最大化赋权法的梯形灰云聚类评价模型，根据梯形灰云白化权函数将复杂系统的评价指标数据划分成若干个可定义类别，判断复杂系统所属的灰类。

Step1：确定指标值矩阵。对于多方案多指标问题，设方案集T={t1,t2,…,tm}，指标集P={p1,p2,…,pn}，评价灰类k∈V={1,2,…,g},g∈R+，记xij=xj(ti)(i=1,2,…,m,j=1,2,…,n)为方案ti下指标pj的值，则方案集T关于指标集P的指标值矩阵为：

(10)

Step2：数据无量纲化。一般选用极小化无量纲化法处理，表达式如下：

(11)

Step3：确定各指标灰云模型数字特征并构造白化模型。首先给出各指标的分级标准，根据指标的分级标准确定指标灰类白化模型所属的阈值区间，根据式(5)计算熵、超熵，然后根据梯形云生成算法由各白化模型的数字特征生成各指标的白化模型。

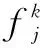
(12)

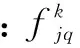
Step5:计算指标的评估结果向量。

(13)

4 算例验证与灵敏度分析

文中主要将基于改进离差最大化赋权法的梯形灰云聚类评估模型应用于大气质量评估中，探讨梯形灰云聚类评价方法与常规的灰色聚类方法[12]的不同点及其先进性。

4.1 灰云聚类评价模型算例

文中以2004-2013年福州市大气环境质量评价作为应用实例，选择SO2,NO2,PM10这三个指标作为评价指标，评价指标数据来源于2004-2013年环境质量公报,监测数据来源于官方公布数据。

大气环境质量被划分为3个等级，表1为3个指标的各标准等级的取值，表2为大气污染指标监测数据。

表1 大气环境质量评价标准

表2 大气污染指标监测数据

将实测数据进行无量纲化处理，借助Matlab软件获得各年份下的指标相对重要性判定矩阵。根据各判定矩阵进行求取最大模特征根及相应向量的计算，再将所得的特征向量单位化后得到的就是指标间相对重要性的权重。

根据改进离差最大化赋权法的灰云白化权函数及评价指标在大气质量中的权重值，按照文中所建立的灰云聚类综合评价模型，对2004-2013年福州市的大气环境质量进行评价，评价结果如表3所示。

表3 基于灰云白化函数的灰聚类综合评价结果

4.2 评价结果及分析

为分析梯形灰云聚类评估模型的可行性、可靠性及梯形灰云聚类综合评价方法的优缺点，文中采用常规的指数型灰色聚类评价方法[13]对福州大气质量进行评价，评价结果如表4所示。

表4 常规指数型灰聚类模型综合评价等级的判定

对比表3和表4可以看出，2004-2013年两种方式的评估结果基本一致。对于2013年，常规的指数型灰聚类评估模型评估结果为一级，梯形灰云聚类评估模型评估结果为二级。结果表明，改进后的梯形灰云聚类评估模型评估结果与福州市环境质量公报发布的大气环境质量等级一致，也证明了该梯形灰云聚类评估模型的可行性。

4.3 灵敏度分析

指标样本评估数据来自客观事物的实际情况或是评估者的主观判断。随着时间的推移，客观事物可能会发生变化，人们的主观意识也可能发生改变；因此，会引起被评估样本矩阵中的数据发生变化，从而有可能引起评估排序结果的改变。评估者必须进行评估结果的灵敏度分析[14-15]，以便掌握决策参数的变化对决策结果的影响，从而做出正确的判断。

设评估模型中有m个评估对象，n个评估指标，第i个评估对象的第j个指标值记为xij。对于第j个指标值，分析当所有评估对象都按照一定百分比增加或减小时的情形。设定变化初始值l0，每次变化的步长为Δl，计算获得新的评估结果，比较新的评估结果与变化前的评估结果是否一致，一旦不一致就停止循环，此时的li就是该指标临界点的阈值。

根据计算流程，对模型进行多目标评估的灵敏度分析。将分别选取SO2、NO2、PM10的样本监测数据设定为变化初始值，步长为样本数据的0.01倍。当指标增大时，变化后样本数据为初始值与步长的和；当指标减少时，变化后样本数据为初始值与步长的差。一直循环，直到样本数据变化后的评估结果与变化之前相差太大即停止。

以SO2、NO2为例，样本数据变化后的评估结果与变化前评估结果的一致性比较如图1和图2所示。

图1 SO2一致性对比

由于时空局限性，大气环境各指标的实际测量数据存在一定范围内的差异，这个范围称作指标的阈值范围。在该范围内，指标实验数据的选取不影响环境质量的评估结果。阈值范围越大说明实验评估结果越稳定。

图2 NO2一致性对比

从图中可以看出，SO2、NO2的阈值取值范围，灰云模型均大于传统指数模型，PM10经计算可得类似结果,说明梯形灰云评估模型比传统指数模型更加稳定。

5 结束语

文中建立了基于改进离差最大化赋权法的梯形灰云聚类评价模型。结合层次分析法改进离差最大化赋权法，确定了各方案中指标的重要程度。通过梯形灰云模型有效解决了大气质量评估过程中的信息不完全性、模糊性和随机性等不确定因素，提高了评估模型的灵敏度，同时也是梯形灰云模型在大气环境质量评价领域的新应用。

[1] 周 辉,杨洪耕,吴传来.基于灰色聚类的电能质量综合评估方法[J].电力系统保护与控制,2012,40(15):70-75.

[2] 崔凯旋,石 全,胡起伟,等.基于梯形云模型的装备保障训练效果评估研究[J].计算机仿真,2013,30(5):306-310.

[3] 李德毅,刘常昱.论正态云模型的普适性[J].中国工程科学,2004,6(8):28-34.

[4] 钟振宇,柴立元,刘益贵,等.基于层次分析法的洞庭湖生态安全评估[J].中国环境科学,2010,30(S):41-45.

[5] 张 荣,刘思峰,刘 斌.基于离差最大化客观赋权法的一般性算法[J].统计与決策,2007(24):29-31.

[6]ShiY,LiuH,SunJ.Thecloudmodelbasedongreysystemtheoryandapplicationoneffectivenessevaluation[M]//IntelligentComputingTheories.Berlin:Springer,2013:31-38.

[7] 王雁凌,张雪佼,阎敬民.基于变权灰云模型的风电场并网技术性综合评价[J].电网技术,2013,37(12):3546-3551.

[8]WangP,ZhangSY,ChenXJ.Anovelreputationreportingmechanismbasedoncloudmodelandgraysystemtheory[J].InternationalJournalofAdvancementsinComputingTechnology,2011,3(10):75-77.

[9] 蔡红梅,陈剑勇,苏浩益.基于灰云模型的电力变压器故障诊断[J].电力系统保护与控制,2012,40(12):151-155.

[10] Chen Y.The comprehensive ranking evaluation of flood disaster based on grey-cloud whitening-weight function[C]//Proc of 2011 international conference on electronic & mechanical engineering & information technology.[s.l.]:[s.n.],2011:1932-1934.

[11] 蒋建兵,梁家荣,江 伟,等.梯形云模型在概念划分及提升中的应用[J].计算机工程与设计,2008,29(5):1235-1237.

[12] 范良千.流域非点源贡献率核定及总量负荷分配研究[D].杭州:浙江大学,2011.

[13] Guo L,Shen M.The identification and evalution of new energy industry cluster based on location quotient and NESS model:taking Zhejiang Province as an example[J].Science of Science & Management of S & T,2013,34(5):70-79.

[14] 柴 栋,童中翔,芦艳龙,等.指标灵敏度分析的飞机空战效能评估方法比较[J].火力与指挥控制,2012,37(6):21-24.

[15] 党耀国,刘思峰,刘 斌,等.聚类系数无显著性差异下的灰色综合聚类方法研究[J].中国管理科学,2005,13(4):69-73.

A Trapezoidal Gray Cloud Evaluation Model Based on Improved Deviation Maximization Weighting Method

FAN Ya-qiong,YAN Xue-feng,CHEN Hai-yan

(Department of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China)

Due to the problem of the deviation maximization weighting method that can’t fully embody the difference of the weight of the index in different schemes and the characteristics of the method of the AHP that can obtain the relative importance of the index by the comparison,the AHP is introduced to improve the maximum weight of the deviation.Meanwhile,owing to the incomplete and uncertain of the amount of information provided by the monitoring data in some areas and the property of cloud theory which is an effective tool for dealing with fuzzy and random information,the whitening weight function is improved by the introduction of the trapezoid cloud model.Thus,a trapezoidal gray cloud clustering evaluation model based on the maximum weight of dispersion is established in this paper.The atmospheric environmental quality of Fuzhou city during the last ten years is assessed by using the improved trapezoidal gray cloud cluster assessment model.Examples show that the results of the model are consistent with the objective reality.The feasibility and practicality of the model are verified by sensitivity analysis.It is the trapezoidal gray cloud clustering evaluation model that provides a new and effective way for the comprehensive evaluation.

trapezoidal gray cloud clustering;improved deviation maximum weight method;atmospheric environment quality;sensitivity analysis

2015-07-16

2015-10-21

时间：2016-03-22

国防科工局“十二五”重大基础科研项目(c0420110005)

范亚琼(1990-)，女，硕士研究生，研究方向为网络与分布计算;燕雪峰，副教授，研究方向为计算机网络、分布交互仿真等；陈海燕，讲师，研究方向为数据挖掘、民航信息化等。

http://www.cnki.net/kcms/detail/61.1450.TP.20160322.1522.082.html

TP311

A

1673-629X(2016)04-0020-05

10.3969/j.issn.1673-629X.2016.04.005