一种基于倒排索引的多维网络存储模型

张志远，徐恒盼

(中国民航大学 计算机科学与技术学院，天津 300300)

一种基于倒排索引的多维网络存储模型

张志远，徐恒盼

(中国民航大学 计算机科学与技术学院，天津 300300)

具有多维属性的实体相互连接构成的网络(如社交网络)称为多维网络，在多维网络上支持联机分析处理具有重要的应用价值。现有方法大都从文件或数据库中逐条读取记录，当数据量很大时，需要多次读取磁盘，导致查询响应时间过长，效率较低。文中提出了一种新的基于倒排索引的多维网络存储模型II-GC(Inverted Index based Graph Cube)，通过将图的拓扑结构和顶点的多维属性存储在倒排索引列表中加快查询速度，并给出了在多维网络上进行聚集查询(cuboid)和交叉查询(crossboid)的算法。在DBLP数据集上的实验表明，该模型较GraphCube的查询效率更高，扩展性更好。

多维网络；图立方体；倒排索引；联机分析处理

0 引 言

随着Web2.0等互联网新概念的飞速发展，大量新型社交网络服务不断涌现，社交网络在人们的生活中扮演着越来越重要的角色。作为一个交叉领域，社交网络研究已经得到国内外学者们的广泛关注。目前对于社交网络的研究多集中于其拓扑结构，如社区划分[1-2]、舆情传播[3]等。在实际应用中，除拓扑结构外，与顶点相关的多维属性信息也非常重要，如统计合著网络中的男女比例及连接关系等。文中主要研究由拓扑结构及与顶点关联的多维属性一起构成的多维网络[4]。

对多维网络进行OLAP[5]分析可展现不同尺度上的网络结构特征，如聚集操作可分析合著网络中不同领域人员之间的网络结构，切片操作可分析某特定领域如数据挖掘学者之间的网络关系。为突破传统OLAP技术无法支持带有图结构的复杂网络分析的限制，近年来研究人员开展了很多相关研究。2007年吴巍[6]提出了Link OLAP的概念，将面向实体的分析扩展为面向连接的分析，以复杂网络可视化为基础，突破了以往传统OLAP系统中单调的二维表格表现方式。同年，Chen等[7]提出了Graph OLAP的概念，将OLAP技术引入到复杂网络分析中，实现了在信息维和拓扑维两种维度上的OLAP操作。2010年，Li等[8]提出了一种适合Graph OLAP的数据仓库概念模型，即双星模型，并提出了信息维聚集算法I-OLAPing和拓扑维聚集算法T-OLAPing。2011年，Li等[9]又在原有基础上提出了基于信息网络数据仓库和信息网络数据立方体的概念，提出了双星座数据模型，实现了信息维和拓扑维的聚集算法以及上卷下钻的OLAP操作。同年，Zhao等[10]详细介绍了一个新的数据仓库模型，即基于图的数据立方体Graph Cube，同时提出了用于Graph OLAP的新的查询方式crossboid(详见定义4)，并讨论了Graph Cube的物化策略。2011年，Qu等[11]提出了一种信息网络拓扑维的框架，并基于此框架提出了更高效的查询方法以及数据立方体的物化策略，对拓扑维在线分析处理(T-OLAP)操作中特定类型度量的优化进行了有针对性的深入分析。

现有的GraphCube OLAP聚集算法研究大多是直接对文件或数据库中的数据进行聚集查询，逐条检索记录，判断是否符合条件。当文件很大时，往往要多次读写磁盘，较为耗时。文中提出了一种新的多维网络存储模型II-GC(Inverted Index based Graph Cube)，通过引入倒排索引技术，把直接对数据库中数据进行的聚集查询转化成倒排索引集合间的交、并运算，不用逐个读取记录，参与运算的数据大幅减少，提高了检索速度。

1 基本概念

定义1：多维网络[4,12]。多维网络是一个形式为G=(V,E,A)的图，其中V是顶点集合，E⊆V×V是边的集合，A={A1,A2,…,An}是与顶点相关联的属性集合。任取v∈V，存在一个多维元组A(v)=(A1(v),A2(v),…,Am(v))，其中Ai(v)是顶点v上的第i个属性，1≤i≤m。

图1是一个社交网络中的多维网络示例。图中有10个顶点，记作v1,v2,…,v10，分别代表社交网络中不同的个体；13条边分别代表个体间的关系。每个顶点均关联一个多维属性元组，记录该个体的基本信息，包括ID，Gender，Location及Profession。所有顶点的多维属性元组集合构成多维属性表，如表1所示。

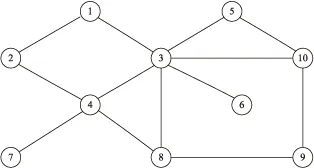
图1 一个社交网络的多维网络图

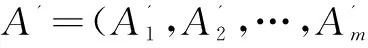
表1 多维属性表

(2)∀u',v'∈V'，其中u'代表[u]，v'代表[v]，令E(u',v')={(u,v)|u∈[u],v∈[v],(u,v)∈E}，若E(u',v')非空，则∃e'∈E代表E(u',v')。边的权重ω(e')=Fe(E[u',v'])，其中Fe()为作用在边上的聚集函数，称e'为聚集边。

以图1中的“社交网络”为例，选取A的一种聚集A'=(Gender，*，*)，以Count()作为顶点和边上的聚集函数，则产生的聚集网络含Male和Female两个聚集顶点，其权重值分别为男女实例的个数，本例中均为5。边的权重代表聚集顶点间的关系，如Female顶点集合{v2,v3,v4,v6,v9}中有三条边连接，即v2v4,v3v4,v3v6，因此其权重为3。

定义3：图立方体[10]。给定多维网络(V,E,A)，根据A的所有可能的聚集产生的聚集网络集合构成图立方体(GraphCube，GC)，其每个聚集网络又被称为cuboid。

仍以图1中的社交网络为例，顶点代表在不同的聚集属性下得到的聚集网络，边代表不同的聚集网络间的父子关系，其中(Gender，Location，Profession)是所有其他聚集网络的基础，(*，Location，Profession),(Gender，*，Profession)及(Gender，Location，*)均可从(Gender，Location，Profession)直接求得。

图2 crossboid查询产生的聚集网络

2 II-GC存储模型

多维网络可看作是具有多维属性顶点的网络图，节点的属性信息可存储在其data域中，也可像表1一样将所有顶点信息存储在一个二维表格中。在进行聚集操作时，两种方式均需要对图进行遍历，时间复杂度为O(n+e)。其中，n是顶点个数，e是边的条数。随着网络规模的增加，这种线性复杂度甚至都是不能忍受的。为此文中提出基于倒排索引的多维网络存储模型，将所有信息存储在顶点的倒排索引和边的倒排索引中，如图3所示。

图3 基于倒排索引的多维网络存储模型

按照广度优先的遍历顺序对点和边进行编号，2.1节中讨论了这种编号方式带来的好处。边的倒排索引按起点和终点分为两组，对如图1所示的无向图，以数字较小的顶点为起点。例如边起点倒排索引中的Male：1,2,11,12表明有四条边的起点中Gender属性为Male。起点倒排索引中的Male和终点倒排索引中的Male交集只含有11这一条边，因此可以确定Male和Male之间的连接边只有一条，正好回答了Male自身连接权重的问题。采用基于倒排索引的存储模型至少有以下几个优点：

(1)将图遍历转换为集合的交并操作，加快了查询速度；

(2)采用倒排索引压缩算法可进一步减少存储空间；

(3)相对于结构复杂的图来说，基于倒排索引的查询更容易并行化。

2.1 模型初始化

将多维网络转换为基于倒排索引的存储模型，初始化算法如下：

输入：一个多维网络G=(V,E,A)；

输出：点倒排索引表N，边倒排索引表E1,E2，边编号索引表EI。

begin

//按广度优先顺序对图节点编号

初始化队列Q，并将v1加入Q;

nodeno←0;设置所有节点为未访问;

whileQ非空{

从队列中取出一个顶点u并标记为已访问;

u.id=++nodeno;

foru的每个未访问过的邻居节点v{

ifv不在Q中则将其加入队列Q;

}

}

//对图广度优先遍历并设置倒排索引表

初始化队列Q，并将v1加入Q;

edgeno←0;设置所有节点为未访问;

whileQ非空{

从队列中取出一个顶点u并标记u为已访问;

for除id外的每一个属性Ai{

N(Ai(u))←N(Ai(u))∪{u.id}；

}

foru的每个未访问过的邻居节点v{

EI[++edgeno]←(u.id,v.id);

for除id外每一个属性Ai{

E1(Ai(u))←E1(Ai(u))∪{edgeno};

E2(Ai(u))←E2(Ai(v))∪{edgeno};

}

ifv不在Q中则将其加入队列Q;

}

}

end

按广度优先顺序对图节点和边进行编号，这样可保证点和边的倒排索引列表按升序排列，为后面的求交操作带来便利。算法相当于对原图进行了两次广度优先遍历，其时间复杂度亦为O(2n+2e)。采用倒排索引格式存储后，原多维网络不必继续保留。若采用的聚集函数为Count()，则边编号索引表EI也可以去掉。由于倒排索引存储的均为整数，和原来使用大量字符串相比存储空间有所减少。需要注意的是，该存储模型对类别较多的列属性(如姓名)而言是低效的，因为这会造成大量的短倒排索引列表，不利于后面的查询操作。

2.2 cuboid查询

以聚集A'=(Gender,*,*)为例，Gender对应的属性值有Male和Female，查看相应的点倒排索引表N得：N(Female)={2,3,4,6,9}，N(Male)={1,5,7,8,10}。说明Female和Male分别有5人。然后再查他们之间的连接关系得：E1(Male)={1,2,11,12}，E2(Male)={5,7,8,9,10,11,13}。两者的交集为{11}，说明以Male为起点和终点的边只有1条。同理可得E1(Female)∩E2(Female)={3,4,6}，说明以Female为起点和终点的边共有3条。连接Male和Female之间的边或者以Male为起点，或者以Female为起点，对应的集合为{E1(Male)∩E2(Female)}∪ {E1(Female)∩E2(Male)}={1,2,5,7,8,9,10,12,13}，说明Male和Female之间有9条边。Cuboid查询算法如下：

输入：倒排索引多维网络IIG=(N，E1，E2，EI)，聚集属性A'；

begin

V'←ø;E'←ø;

//计算所有可能的聚集顶点

Vt1←ø;Vt2←ø;

ifV'为空集{V'←Vt1;continue;}

forV'的每一个元素v'{

forVt1的每一个元素vt1{

Vt2←Vt2∪{v',vt1};

}}

V'←Vt2;Vt1←ø;Vt2←ø;

}

//计算顶点的权重

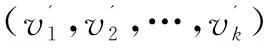
if(T==ø){将v'从V'中删除;continue;}

}

//计算边的权重

forV'的每一个顶点对(u',v'){

if(u'≠v'){

e←e∪e';

}

if(e≠ø) {

{E'←E'∪{(u',v')};

}

}

end

设cuboid聚集网络有m个顶点，每个顶点有k个分量(如Male,Professor)，则算法最多需要2m2k+mk次求交集操作，而实际上会小得多，因为求交集时集合大小随着次数的增加将明显变小，当结果为空时即可停止。

2.3 crossboid查询

以(Gender，*，*)和(*，Location，*)为例，对两个聚集属性依次应用2.2中算法的前两步得6个聚集节点：Male(5)，Female(5)，CA(3)，WA(3)，NY(2)，IL(2)。其中括号内的值为点的权重。然后应用边倒排索引查询连接边，例如Male和CA之间的连接为：(E1(Male)∩E2(CA))∪(E1(CA)∩E2(Male))=([1,2,11,12]∩[2,12])∪([1,2,4,5,6,7,8,13]∩[5,7,8,9,10,11,13])=[2,5,7,8,12,13]。因此Male和CA之间的连接权重为6。crossboid查询算法如下：

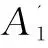
//求S和T的连接边及权重

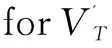
e←e∪e'；

if(e≠ø) {

E'←E'∪{(u',v')};

}

}

}

2.4 双二分查找

倒排索引源于实际应用中需要根据属性的值来查找记录。这种索引表中的每一项都包括一个属性值和具有该属性值的各记录的地址。由于不是由记录来确定属性值，而是由属性值来确定记录的位置，因而称为倒排索引。利用倒排索引查询的时间复杂度主要取决于集合求交的过程，注意到所有的倒排索引列表都是升序排列的，可以采用双二分查找算法[13]提高查找速度。对于两个有序集合D和Q，假设D比Q的元素多。该算法首先在D中对Q的中间值Qmid进行二分查找，若找到则将Qmid添加至结果集R中。无论是否找到，都可以将D和Q划分为两个部分：D1，D2以及Q1，Q2。其中D1和Q1中的所有元素都小于Qmid，D2和Q2中的所有元素都大于Qmid。如此，问题转换为求D1和Q1的交集及D2和Q2的交集。实际过程中可先比较两个集合的最大最小值判断其交叉重叠部分，从而减少比较集合的大小。Ricardo指出，当两个集合的元素个数相差较大时，该算法的复杂度为O(mlg(n))。其中m和n分别为短集合和长集合的元素个数[14]。由于需要进行多次求交运算，结果集合肯定会越来越短，因此适合采用双二分查找。

3 实验结果与分析

3.1 实验数据集

从1969年到2014年的DBLP数据集中选取四个领域的会议文章共289 135篇，按作者统计文章发表情况建立了合著关系网络，含34 259个作者作为顶点，193 902个作者之间的合作关系为边。顶点属性信息为Author、Area、Year、Productive。共包含4个Area，每个Area选取5个代表性会议：数据库(SIGMOD，VLDB，ICDE，PODS，EDBT)、数据挖掘(KDD，ICDM，SDM，PKDD，PAKDD)、信息检索(SIGIR，WWW，CIKM，ECIR，WSDM)和人工智能(IJCAI，AAAI，ICML，CVPR，ECML)。若作者在多个领域发表文章，选择文章数量最多的领域为其Area。Productive根据作者发表的文章篇数分为四个类别：excellent(35篇以上)、good(15到34篇)、fair(3到14篇)以及poor(小于3篇)。

3.2 cuboid查询实验

本小节对比II-GC和GraphCube[10]的cuboid查询在不同规模多维网络上的响应时间。网络边数从1万到6万变化时的cuboid查询响应时间对比如图4所示。

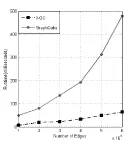
图4 不同规模网络上的cuboid查询对比

可以看出，II-GC比GraphCube上的cuboid查询响应时间短，且随着复杂网络边数的增加，II-GC的查询响应时间变化不大，而GraphCube的查询时间则迅速增加。

聚集维度从1到3变化时，两者的cuboid查询响应时间对比如图5所示。

图5 不同维数上的cuboid查询对比

可以看出，II-GC的cuboid查询响应时间更短，且随着维数的增加，II-GC的查询响应时间呈线性增长，而GraphCube则迅速增加。

实验结果验证了基于II-GC处理cuboid查询的高效性。

3.3 crossboid查询实验

本小节对比II-GC和GraphCube的crossboid查询响应时间。在不同规模网络上的实验结果如图6所示。

图6 不同规模网络上的crossboid查询对比

可以看出，在II-GC的crossboid查询性能较优，且随着网络规模增大，GraphCube上的crossboid查询响应时间呈直线上升，而II-GC的变化则较为平缓。实验结果验证了基于II-GC处理crossboid查询的高效性。

4 结束语

基于倒排索引的多维网络存储模型将逐条对比的查询操作转换为有序集合的交并操作，在减小存储空间的同时优化了查询性能。在DBLP数据集上的实验结果表明，该模型扩展性较好，查询效率较高。当属性值的分类个数较多时，会出现大量短倒排索引，影响查询效率。

[1] 程学旗,沈华伟.复杂网络的社区结构[J].复杂系统与复杂性科学,2011,8(1):57-70.

[2] 张 娜.复杂网络社区结构划分算法研究[D].大连:大连理工大学,2009.

[3] 陈 旭.基于社会网络的WEB舆情系统的研究与实现[D].西安:西安电子科技大学,2010.

[4] 张兰华.复杂网络建模的仿真与应用研究[D].大连:大连理工大学,2013.

[5] Han Jiawei, Sun Yizhou. Mining heterogeneous information networks[C]//Proc of the 16th ACM SIGKDD international conference on knowledge discovery and data mining.[s.l.]:ACM,2013.

[6] 吴 巍.复杂网络可视化与Link OLAP[D].北京:北京邮电大学,2007．

[7] Chen Chen, Yan Xifeng, Zhu Feida,et al. Graph OLAP:a multi-dimensional framework for graph data analysis[J].Knowledge and Information Systems,2009,21(1):41-63.

[8] Li Chuan,Zhao Lei,Tang Jie,et al.Modeling,design and implementation of graph olaping[J].Journal of Software,2011,22(2):258-268.

[9] Li Chuan,Yu P S,Zhao Lei,et al.InfoNetOLAPer:integrating InfoNetWarehouse and InfoNetCube with InfoNetOLAP[J].Proceedings of the VLDB Endowment,2011,4(12):1422-1425.

[10] Zhao Peixiang,Li Xiaolei,Xin Dong,et al.Graph cube:on warehousing and OLAP multidimensional networks[C]//Proc of ACM SIGMOD international conference on management of data.[s.1.]:ACM Press,2011:853-864.

[11] Qu Qiang,Zhu Feida,Yan Xifeng,et al.Efficient topological OLAP on information networks[C]//Proc of the 16th international conference on database systems for advanced applications.Berlin:Springer-Verlag,2011:389-403.

[12] 邵连龙,尹 沐.基于DBLP的多维异质网络Graph Cube设计与实现[J].计算机应用研究,2014,31(3):720-724.

[13] Baeza-Yates R.Experimental analysis of a fast intersection algorithm for sorted sequences[C]//Proceedings of the 12th international conference on string processing and information retrieval.[s.l.]:[s.n.],2005:13-24.

[14] Baeza-Yates R.A fast set intersection algorithm for sorted sequences[C]//Proceedings of the 15th annual symposium on combinatorial pattern matching.[s.l.]:[s.n.],2004:400-408.

A Multi-dimensional Network Storage Model Based on Inverted Index

ZHANG Zhi-yuan，XU Heng-pan

(School of Computer Science & Technology,Civil Aviation University of China, Tianjin 300300,China)

A network such as social network linked by entities with multiple attributes is called multi-dimensional network.OLAP query on multi-dimensional network has an important application value.Most existing methods read records one by one from a file or a database.When a lot of data involved,these methods need more I/O time,thus leading to large query response time and low query efficiency.A new multi-dimensional network storage model based on inverted index is presented,called II-GC (Inverted Index based Graph Cube).It speeds up the process by constructing inverted index both on topological graph and multiple attributes.Algorithms about cuboid and crossboid are also introduced.Experimental results on DBLP show that this model is more efficient and scalable than GraphCube.

multi-dimensional network;graph cube;inverted index;OLAP

2015-07-15

2015-10-21

时间：2016-03-22

国家自然科学基金资助项目(61201414,61301245,U1233113)

张志远(1978-)，男，副教授，硕士研究生导师，研究方向为数据挖掘；徐恒盼(1987-)，女，硕士研究生，研究方向为数据仓库技术。

http://www.cnki.net/kcms/detail/61.1450.TP.20160322.1521.070.html

TP391.9

A

1673-629X(2016)04-0025-06

10.3969/j.issn.1673-629X.2016.04.006