面向计算机专业的“离散数学”课程改革与探索
魏立斐 王晓明 王春华

摘要:“离散数学”是计算机科学与技术、软件工程、通信工程、网络空间安全等信息类本科专业的核心基础课之一,在计算机科学与技术等专业课程体系结构中起到非常重要的理论支撑作用。本文分析了计算机专业开设“离散数学”课程中存在的一些问题,从教学目标、教学内容、教学方式等方面,建议在教学时结合计算机相关领域中的实际例子,深入浅出地传授“离散数学”中的理论知识点,并采用理论教学结合编程练习,激发学生的兴趣,提高教学质量。
关键词:离散数学;课程改革;问题驱动;编程实现;结合应用
中图分类号:G642.0 文献标志码:A 文章编号:1674-9324(2016)08-0127-03
一、引言
离散数学(Discrete Mathematics)是计算机科学与技术、软件工程、通信工程、网络空间安全、信息与计算科学等信息类本科专业的核心基础课之一,在计算机科学与技术等专业课程体系结构中起到非常重要的理论支撑作用[1]。因此,离散数学早在1977年就已被美国电子电气工程师协会(IEEE)确定为计算机专业的核心课程。2001年又被IEEE协会和美国计算机协会(ACM)联合认定为计算机专业的第一核心主干课程[2]。
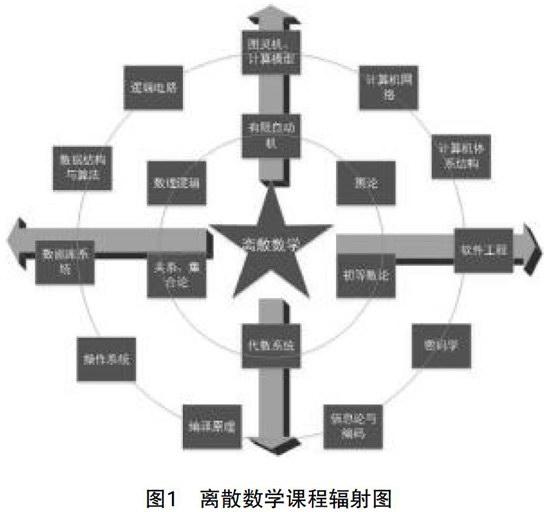
由于电子计算机存储空间与计算能力的限制,计算机相关的很多领域都使用到了离散结构的概念。如计算机中的任何一个变量都是离散变量,计算机中的图片都是以离散像素的形式存在。所有的存储和通信的数据本质上都是0和1构成的。因此,“离散数学”的教学内容与计算机硬件和软件都有着密切的关系。“离散数学”采用严格形式化的数学语言来描述离散系统的状态、关系和变化过程,是进行定性定量分析和逻辑推理的工具,可以为计算机系统处理离散对象的状态及变换提供有效的描述[3]。离散数学不仅是计算机专业的核心课程,更是“数据结构”、“算法设计与分析”、“数据库原理”、“数字逻辑(数字电路)”、“编译原理”、“信息安全”、“操作系统”、“并行计算”等一系列课程的先导课程。如图1所示,离散数学中核心的六个部分:数理逻辑、关系集合论、代数系统、图论、初等数论和有限自动机,分别衍生出计算机的学科体系架构。
通过离散数学的教学,使学生掌握课程的基本概念和基本原理,采用严格的数学方法,培养学生的抽象思维能力和逻辑推理能力,为从事计算机的科研与应用提供必要的描述工具和理论基础,培养学生利用计算机分析问题、解决问题的能力。
根据教育部“离散数学”教学指导委员会建议,目前国内离散数学的教学大致可以分为三个层次:科学型、工程型、应用型[4],对应的学时分别为108、90、72。科学型人才培养的目标要求学生有坚实的数学基础,较强的抽象思维能力,形式化描述能力和推理、分析能力;工程型人才的目标是要求学生有较好的数学基础,能综合运用离散数学中的理论和模型去分析问题和解决问题,兼顾计算机科学和计算机应用,内容较为宽广深入;应用型人才目标则要求学生能够运用典型的离散模型,进行系统建模与软件集成[5]。针对不同的教学内容与教学要求,需要采用“因材施教,分流培养”的教学理念与策略。
然而,在实际的教学过程中,离散数学的教学课时量常常被压缩,一般正式授课时间约为48学时。如何在有限的时间里充分地把知识传授给学生,将能力传播给学生,给离散数学的教学提出了新的挑战。一些高校采用减少学时数量、降低考试难度,这样会造成学生无法认识到“离散数学”在计算机专业的课程架构中的重要地位,导致“离散数学”的教与学越来越边缘化[3]。
为此,笔者在对“离散数学”多年的观察与教学的基础上,对本科阶段计算机专业的“离散数学”课程存在问题进行了深入剖析,并给出了一些初步的建议。
二、存在的问题
笔者在近几年的“离散数学”授课过程中,发现不少学生在课程学习与能力培养方面容易存在以下三个问题。
(一)课程学时少,理论难度大
绝大多数的高校开设“离散数学”的学时有限,往往比“教指委”给出的时间少,一般在48学时,难以完整地开展包括数理逻辑、集合论、代数结构、图论、初等数论和形式语言与自动机等内容的教学,往往仅对前四部分(甚至更少)的内容展开教学,初等数论和形式语言与自动机部分由于难度较大,将作为选学内容。
(二)课程辐射不够,相互割裂,学生畏难情绪严重
在实际教学中,很多高校把“离散数学”作为一门数学课,由数学系教师作为主讲教师,采用纯数学经典的“定义—定理—证明—习题”的教学模式[6],忽视了“离散数学”在计算机中的应用背景,让学生感到恐惧与反感,因其未能从“高等数学”与“线性代数”等课程的学习思路和模式中走出来,从而降低了学习兴趣,最终影响教学质量。
(三)理论学习与计算机实践相互割裂
对于计算机专业的学生,需要将所学的理论知识与计算机编程相互关联起来,不能将计算机工具与“离散数学”的知识点强行割裂,如果将理论学习与计算机实践相互割裂,只会使学生纸上谈兵,实际操作能力不能得到有效提高。
三、课程的建议
1.教学手段多样化,凝练重点知识。首先要讲清楚什么是离散的概念,为什么要引入离散的概念,重点介绍离散数学的思维方式和解题思路,消除学生反感、对立的情绪。针对大学生已普及手机等智能移动设备的现状,对于重要的知识点,建议采用微视频、微课的形式,供学生利用点滴课余时间,反复理解,对课堂知识的重、难点进行再现,充分互动,达到知识传递的效果,并及时采用微学堂、微试题等形式,对教学效果进行反馈。
2.以点带线,线面结合,增加课程关联度介绍,建议梳理计算机专业本科课程,与“离散数学”之间建立对应联系。比如在数字电路设计中,使用“与非”门和“或非”门设计逻辑线路,代替单一的“非”门、“与”门和“或”门的组合;利用等值演算,可大幅度优化逻辑线路。再如利用哈密顿图求解最短路径问题和旅行商周游问题,利用基于最优二叉树的哈夫曼算法来优化编码并提高通信效率;等等。
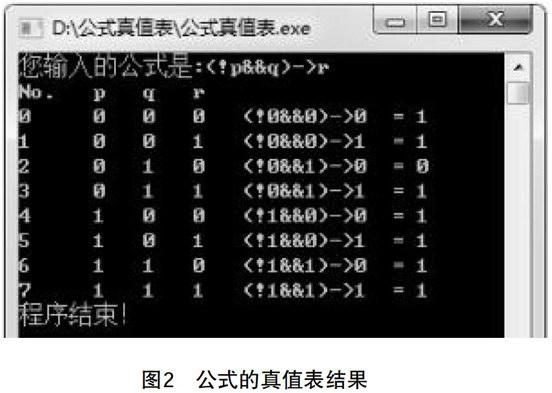
3.编程实现。离散数学作为计算机相关专业的一门基础课,必须与学生已有的基础课(如程序设计语言等)相互关联,使得学生学以致用。开展离散数学中常见算法的编程实现,如利用C/C++语言实现公式真值表的输出:对于给定的公式,判断其合法性之后,给出其真值表。如“a”到“z”单个小写字母表示变元,运算符用!(非)、&&(合取)、||(析取)、->(蕴含)、<->(等价)、()(英文圆括号)表示。程序运行如图2所示。
类似的,结合离散数学课程,笔者推荐如下算法:集合的笛卡尔积计算,欧拉图的判定,关系的判定,自反、对称、传递闭包的计算。如利用C/C++语言中二维数组的运算,实现自反、对称、传递闭包的矩阵的输出,从而有助于判断关系的性质,程序运行如图3所示。
对于Dijkstra算法、Kruskal算法、Prim算法等,在后续的“数据结构与算法”课程中将有详细的算法描述,在离散数学课程中不必要求实现。
四、结语
“离散数学”既作为计算机大类专业的一门重要专业基础课,又在计算机领域具有广泛的应用。有人说:没有“离散数学”就没有计算机理论,也就没有计算机科学[7],足以证明它的重要性。本文针对计算机专业知识体系的结构特点,提出在教学时结合计算机相关领域中的实际例子,深入浅出地传授“离散数学”中的理论知识点,采用理论教学结合编程练习,激发学生的兴趣,提高教学质量。近几年,笔者通过实际教学的检验,该教学方法效果良好,值得借鉴与推广。
参考文献:
[1]屈婉玲,王元元,傅彦,张桂芸.“离散数学”课程教学实施方案[J].中国大学教学,2011,(1):39-41.
[2]帕力旦·赛力提尼牙孜,阿力木.计算机专业离散数学课程教学改革探讨与实践[J].现代教育技术,2009,19(13):262-264.
[3]胡慧君,刘茂福.离散数学对计算机专业系统知识的辐射作用[J].计算机光盘软件与应用,2013,(13):188-189.
[4]教育部高等学校计算机科学与技术教学指导委员会.高等学校计算机科学与技术专业核心课程教学实施方案[M].北京:高等教育出版社,2009.
[5]高志华,贲可荣,刘霞.离散数学课程内容及学习方法探讨[J].计算机教育,2011,(13):107-109.
[6]莫愿斌.凸显计算机专业特色的离散数学教学研究与实践[J].计算机教育,2010,(14):111-114.
[7]离散数学在计算机科学中的作用和应用[EB/OL].
http://www.xzbu.com/9/view-4944068.htm

