基于无迹粒子滤波的电网动态谐波估计
江 辉,陈 笠,帅士奇,彭建春
1)深圳大学光电工程学院,广东深圳 518060;2)深圳大学机电与控制工程学院,广东深圳 518060

Received:2015-11-05;Accepted:2015-12-30
Foundation:National Natural Science Foundation of China (51477104);Shenzhen Science and Technology Research Foundation for Basic Project (JCYJ20140418193546100)
† Corresponding author:Professor Jiang Hui. E-mail: huijiang @szu.edu.cn
Citation:Jiang Hui, Chen Li, Shuai Shiqi, et al. Estimation of dynamic harmonics in power systems based on unscented particle filter [J]. Journal of Shenzhen University Science and Engineering, 2016, 33(1): 80-88.(in Chinese)

【电子与信息科学 / Electronics and Information Science】
基于无迹粒子滤波的电网动态谐波估计
江辉1,陈笠1,帅士奇1,彭建春2
1)深圳大学光电工程学院,广东深圳 518060;2)深圳大学机电与控制工程学院,广东深圳 518060
摘要:提出一种基于无迹粒子滤波(unscented particle filter, UPF)算法的电网动态谐波估计方法.通过无迹卡尔曼滤波算法得到电网动态谐波状态量的估计值和协方差,运用这些结果改进传统粒子滤波算法的重要密度函数,采用粒子滤波算法得到电网动态谐波的最优估计值.该方法克服了无迹卡尔曼滤波算法(unscented Kalman filter, UKF)对噪声要求为高斯分布的限制和传统粒子滤波(particle filter,PF)算法易退化的缺点,保留了UKF对非线性问题的较好处理和PF强抗干扰性能力.仿真结果表明,在高斯噪声和非高斯噪声情况下,UPF算法得到的电网动态谐波幅值、相位的估计值都更接近真实值.
关键词:电力系统;电能质量;动态谐波估计;粒子滤波; 无迹卡尔曼滤波;无迹粒子滤波
电网动态谐波是衡量电网电能质量的一个重要指标[1],对动态谐波的有效治理有助于电网电压的实时监控,准确掌握电压的动态变化,从而采取有效的技术手段对电网电压进行调节.为此,肖湘宁等[2]应用峰值电压法和基波分量法等进行电压凹陷的检测.江辉等[3]提出一种基于小波变换和改进S变换的电压扰动分类方法.丁宁等[4]采用有效值法(root mean square,RMS)分析不同情形下电压凹陷的情况[4].王效孟等[5]提出一种改进的有效值法——半周期有效值(half a cycle of RMS,HRMS)法对电压扰动进行检测,该方法相比传统的有效值法,检测误差更小,延时更短.秦英林等[6]给出了基于奇异值分解技术的电压扰动检测方法,对信号进行线性分解,得到扰动发生的起点和终点时刻.侯世英等[7]采用αβ求导检测法来检测单相电压骤降特征量.Singh等[8]利用双线性递归最小二乘法(bilinear recursive least square, BRLS)对静态谐波和动态谐波的幅值、相位进行估计.任文林等[9]提出一种基于卡尔曼滤波(Kalman filter,KF)的电压扰动检测方法.闵伟等[10]给出一种改进型Sage-Husa卡尔曼滤波电压暂降检测方法,实时更新系统噪声和量测噪声方差,提高了滤波的稳定性和计算速度.卡尔曼滤波是基于线性系统提出的,但实际中广泛存在的是非线性系统,从而卡尔曼滤波在电能质量分析中存在困难.扩展卡尔曼(extended Kalman filter,EKF)[11]将非线性系统线性化,文献[12-13]运用EKF算法对电网频率进行估计.但EKF算法是对非线性函数的泰勒展开式截取实现线性化,且需要计算Jacobian 矩阵的导数,对于高维的数据处理非常复杂.因而,Julier等[14]提出无迹卡尔曼滤波(unscented Kalman filter,UKF),通过一组精确选择的Sigma点匹配随机量的统计特性,UKF没有Jacobian矩阵计算问题,使算法的实现比EKF 更为容易,估计精度更高.
UKF模型要求系统的状态噪声和量测噪声为高斯分布,才能得到最优的状态估计,当条件不符合时其滤波和预测精度就很难得到保证.基于粒子群优化的无迹卡尔曼滤波算法(particle swarm optimized unscented Kalman filter, PSOUKF)[15]采用粒子群算法优化高斯噪声下的状态噪声和量测噪声协方差,提高了估计精度,但是仍对非高斯噪声情形下预测精度难以保证.粒子滤波(particle filter,PF)[16]突破了卡尔曼滤波的理论框架,系统的状态噪声和量测噪声不再受高斯分布限制,被广泛用于机动目标跟踪[17]、人导航与定位[18]、工业过程与监视[19]等非线性、非高斯的情形中.无迹粒子滤波(unscented particle filter,UPF),结合UKF和PF算法的优点,利用UKF对非线性的处理能力以及PF的强抗干扰能力,因而对强干扰性的非线性系统有良好的滤波效果.本研究运用UPF对电网动态谐波进行估计.
1谐波分析模型
一个含噪声和衰减的N次谐波信号,离散化后可表示为[20]

Adcexp(-αdckTs)+μ(k)
(1)
其中, N为谐波的次数; An为幅值; ωn=n2πf0, f0为基波频率; φn为谐波的相位; Ts为采样周期; k=t/Ts; Adcexp(-αdckTs)为衰减部分, Adc和αdc是常量; μ(k)是加入的随机噪声.将Adcexp(-αdckTs)用二阶泰勒公式近似展开,可得
Adcexp(-αdckTs)=Adc-AdcαdckTs
(2)
将式(2)代入式(1),则

Adc-AdcαdckTs+μ(k)
(3)
式(3)可表示为式(4)的量测方程形式
y(k)=H(k)X(k)+μ(k)
(4)
其中,H(k)=[sin(ω1kTs)cos(ω1kTs)sin(ω2kTs)cos(ω2kTs) …sin(ωNkTs)cos(ωNkTs)1-kTs]为测量转移矩阵;状态量可表示为
X(k)=[X1(k)X2(k)…X2N-1(k)
X2N(k)AdcAdcαdc]T
(5)
该处X2N-1(k)=ANcosφN, X2N(k)=ANsinφN. 根据式(5)可将谐波信号状态方程表示为
X(k+1)=F(k)X(k)
(6)
由状态量X(k), 可得各次谐波的幅值及相位分别为
(7)
(8)
2无迹粒子滤波
2.1UKF
UKF由EKF发展而来,是对卡尔曼滤波的一种改进算法,不需要像EKF那样要求把非线性系统线性化,也不需要计算Jacobian矩阵.其主要思想是,在确保采样均值和协方差前提下,选择一组样本点(sigma点集),每个样本点都有自己的状态值和加权值,将非线性变换应用于采样的每个sigma点,得到非线性转换后的sigma点集,从而得到新的均值和协方差[14].
2.2UPF
PF[21]是一种基于蒙特卡罗的近似贝叶斯滤波算法,其主要思想是,根据系统状态量的经验条件分布,寻找一组在状态空间里传播的随机样本集合(这样的样本集合称为粒子),然后根据量测不断地改变粒子的权重和位置来修正最初的经验条件分布,实质是用粒子及其权重组成的离散随机测度来近似系统随机变量的概率密度函数,从而获得最小方差估计.
在常规算法中,常选择先验概率密度作为重要密度函数,这样虽然便于实现,但也易丢失k时刻的测量值,使状态量过分依赖模型,若模型不准确将不能有效估计真实分布.随着计算的推进,易引起粒子算法退化.为避免发生退化,在引入重采样的同时,还可选择一个适合的重要密度函数.
UPF利用UKF得到一个建议分布函数,然后利用该函数来代替PF算法中的重要密度函数, UPF算法主要包括选取sigma采样点、状态以及量测的更新、粒子集和权值的计算[22]4个方面.
非线性系统状态方程和量测方程分别为
xk=F(xk-1, νk)
(9)
yk=H(xk-1, wk)
(10)
其中, xk, νk, yk和wk分别是系统在k时刻的状态量、状态噪声、量测量和量测噪声; F和 H分别是系统状态转移矩阵和量测转移矩阵.
设 xik-1和 Pik-1是k-1时刻状态量 xk-1的均值和误差协方差, L是 xik-1的维数,粒子滤波中取M个粒子数, i=1,2,…,M, j=0,1,…,L. UPF算法计算步骤为
1)选取每个粒子的sigma采样点.
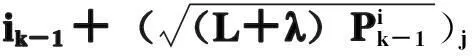

(11)
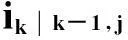
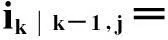
(12)

(13)


(14)
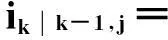
(15)

(16)


(17)

(18)
3)量测更新.计算状态量测协方差Pxkyk和UPF算法的增益KUPF,得到估计值 xik及误差协方差 Pik分别为


(19)
KUPF=PxkykP-1ykyk
(20)
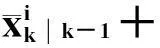
(21)

(22)
至此,利用UKF算法得到每个粒子在k时刻的估计值和误差协方差 xik和 Pik, 从而得到重要密度函数为

(23)
其中, N(·)表示高斯函数,由此重要密度函数中采样粒子,计算权值并归一化.采样粒子为
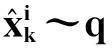
(24)
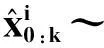
(25)
4)重采样按照下式近似计算有效粒子数.
(26)

5)状态估计.

(27)
方差估计为

(28)
返回步骤2)进行递推计算,直到结束.
3基于无迹粒子滤波的谐波估计
1)根据前述谐波模型,对式(5)中的状态量设置初始值,从每个状态量中抽取M个粒子.设置状态噪声协方差Q、 量测噪声协方差R和状态误差协方差初始值P0.
2)对每个粒子,根据式(11)至式(22)计算k刻的状态量的估计值 xik和协方差 Pik.

4仿真分析
为比较分别采用KF、UKF和UPF的谐波估计方法的性能,本研究采用均方误差(mean square error,MSE)来衡量估计的效果.第k个时刻的均方误差定义为
(29)
其中, N为状态量的维数; yi′和yi分别是该时刻预测值和理论值的第i个分量.显然,均方误差越小说明估计效果越好.
本研究是在Matlab R2007版本下进行仿真,采样频率fs=2.5 kHz.
4.1静态谐波估计
含有噪声的谐波电压信号表达式描述为
y(t)=1.2sin(ωt+75°)+0.8sin(3ωt+55°)+
0.2sin(5ωt+45°) +μ(t)
(30)
其中, μ(t)是随机高斯噪声,其均值为0,方差为1; t=0.2 s,采样间隔ts=1/2 500 s.根据式(4)和式(6), L=6, M取100,3种方法得到的5次谐波幅值及相位的结果如图1和图2.
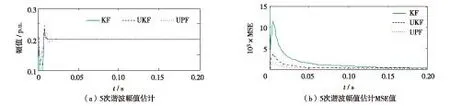
图1 5次谐波幅值估计及MSE值Fig.1 Amplitude estimation and MSE for the 5th harmonic signal
在图1和图2中,可明显看出,基于UPF的谐波估计方法较其他两种方法能更迅速地估计出真实值,且更接近真实值.表1为在0.05 s时刻时,各方法静态谐波幅值与相位估计结果的对比.由表1可见,在0.05 s时,5次谐波的幅值的实际值为0.2 p.u..基于KF、 UKF 和UPF估计的幅值分别为0.191 3、0.201 5和0.201 0 p.u.,其相对误差分别为4.35%、0.75%和0.51%,可见基于UPF方法的估计效果要优于其他两种方法.对基波、3次谐波幅值和相位估计与分析有相同结果.
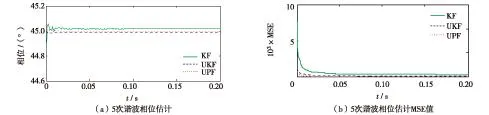
图2 5次谐波相位估计及MSE值 Fig.2 Phase estimation and MSE for the 5th Harmonic signal

算法基波幅值/p.u.相位/(°)3次谐波幅值/p.u.103×MSE幅值相位/(°)103×MSE相位5次谐波幅值/p.u.103×MSE幅值相位/(°)103×MSE相位实际值1.2750.8550.245KF1.199375.03160.78280.8055.02471.20.19131.4045.01860.7UKF1.199775.00420.79010.3254.97410.70.20150.0544.99110.2UPF1.200174.99580.79910.1055.00180.50.20100.0245.00030.1
4.2动态谐波幅值估计
动态谐波电压信号(幅值随时间变化的信号),可描述为
y(t)=[1.2+a1(t)]sin(ωt+75°)+
[0.7+a2(t)]sin(3ωt+55°)+
[0.3+a3(t)]sin(5ωt+45°)+μ(t)
(31)
其中,ω=2πf; f=50Hz; μ(t)是随机高斯噪声,其均值为0,方差为1.
(32)
其中, f1=2.0 Hz; f3=5.0 Hz; f5=7.0 Hz.
采用KF、UKF和UPF对该含有噪声的动态谐波基波、3次谐波和5次谐波幅值的估计和其分别对应的MSE值如图3至图5,本研究仅给出了系统中含3次和5次动态谐波时,采用本方法的谐波幅值估计,对于系统含更多种谐波分量时,本方法同样适用,仿真都能在2~3个周波时间(0.04~0.06 s)内较好估计出动态谐波信号幅值.限于篇幅从略.

图3 基波幅值估计及MSE值Fig.3 Amplitude estimation and MSE for fundamental harmonic
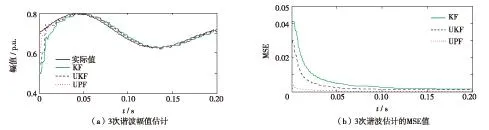
图4 3次谐波幅值估计及MSE值Fig.4 Amplitude estimation and MSE for the 3rd harmonic
表2为0.05 s时采用KF、UKF和UPF的动态幅值估计结果对比.由表2可见,基于UPF的方法估计的幅值更接近实际值,其MSE值也均小于其他两种方法.
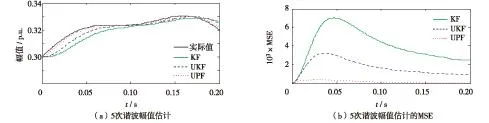
图5 5次谐波幅值估计及MSE值Fig.5 Amplitude estimation and MSE for the 5th harmonic

谐 波实际值KF幅值/p.u103×MSEUKF幅值/p.u103×MSEUPF幅值/p.u103×MSE基波1.32721.32006.01.20364.21.19810.813次谐波0.79430.79584.90.79562.40.79520.305次谐波0.32170.31756.70.31762.80.32130.18
分别加入20和40 dB信噪比的高斯噪声后,在0.05 s时基于KF、UKF、UPF的谐波估计方法对基波幅值估计的MSE值分别为1.7×10-3、1.4×10-3、0.4×10-3和1.5×10-3、1.11×10-3、0.22×10-3,此时理论幅值应为1.327 2 p.u.,基于UPF估计的MSE值小于另外两种方法.为体现本研究所提算法的优越性,对于非高斯噪声情况下,将本方法与基KF、基于UKF和文献[15]提出的基PSOUKF方法进行比较,加入非高斯噪声u(t)=Γ(0.3, 0.2), 4种方法对基波在0.05 s时刻的幅值估计对比如表3.
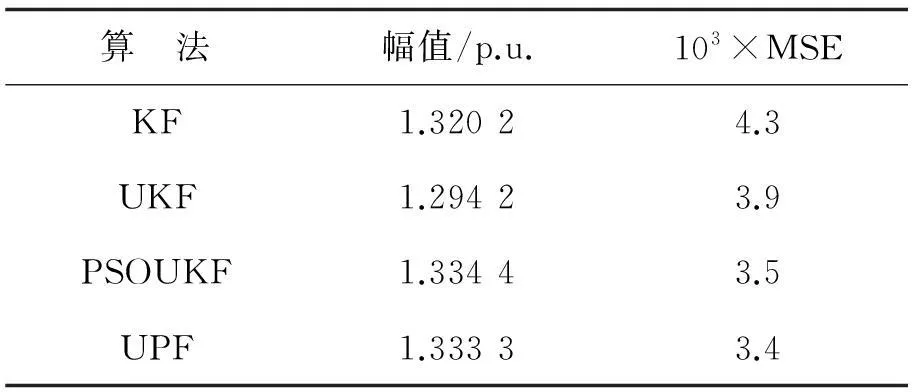
表3 t=0.05 s时非高斯噪声下幅值估计
加入的非高斯噪声为伽马分布时,与加入高斯噪声相比,各方法估计的幅值(真实值为1.327 2 p.u.)精度降低,但从各种方法估计幅值的MSE值可以看出,本研究提出的基于UPF的谐波估计方法相比基于PSOUKF的谐波估计方法在非高斯情形下,对非高斯(伽马分布)的情形具有更强的处理能力,是各种方法中效果最好、精度最高的一种算法.对于其他非高斯噪声情况,我们也进行了仿真,结论相同,限于篇幅,不再列举.
4.3动态相位估计
动态谐波信号(相位随时间变化而变化)的信号可描述为
y(t)=1.2sin[ωt+a1(t)+75°]+
0.5sin[3ωt+a2(t)+55°]+
μ(t)
(33)
其中, ω=2πf, f=50Hz; μ(t)是随机高斯噪声,其均值为0,方差为1;
(34)
这里, f1=2.0 Hz; f3=5.0 Hz; f5=7.0 Hz.
表4为t=0.05 s时基波和3次谐波的动态相位估计效果对比,图6和图7为基波和3次谐波相位的估计波形图.

表4 t=0.05 s时动态相位估计
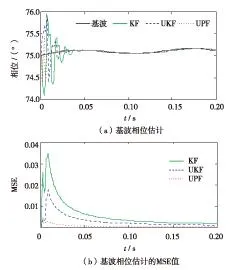
图6 基波相位估计及MSE值Fig.6 Phase estimation and MSE for fundamental harmonic

图7 3次谐波相位估计及MSE值Fig.7 Phase estimation and MSE for the 3rd harmonic
由表4、图6和图7可见,对于谐波的相位估计,本算法也优于KF和UKF方法.加入非高斯噪声u(t)=Γ(0.3, 0.2)后, t=0.05 s时基波相位实际值应为75.127 2°,本研究所提出的基于UPF的谐波估计方法与文献[15]提出的基于PSOUKF的谐波估计方法对该时间基波相位的估计值分别为75.128 4°和75.095 1°,MSE值分别为0.001 1和0.001 4,相对误差分别为0.002%和0.043%,各项数据表明,在非高斯噪声下,基于UPF的估计效果要优于基于PSOUKF的方法.
仿真结果说明,在同样的高斯噪声下,基于UPF的谐波估计方法对谐波各时刻幅值以及相位的估计所得到的MSE值均要小于其他两种方法,其效果要好于基于KF和UKF的方法,在非高斯噪声下,也表现出更强的估计能力.
结语
本研究提出一种基于UPF的动态谐波幅值及相位的估计方法,仿真结果表明,本研究所提出的方法其性能总体优于基于KF和UKF的方法,对于静态和动态谐波以及在不同噪声下都具有良好的估计精度,对于非高斯噪声,所提方法较文中所提其他方法表现出更强的估计能力.目前,如何用UPF算法对电网频率以及间谐波的进行估计,如何选择最合适的重要密度函数和算法的收敛性研究,尚有待深入研究.

引文:江辉,陈笠,帅士奇,等.基于无迹粒子滤波的电网动态谐波估计[J]. 深圳大学学报理工版,2016,33(1):80-88.
参考文献/ References:
[1] 程浩忠,艾芊,张志刚,等.电能质量[M].北京:清华大学出版社,2006:11-14.
Cheng Haozhong, Ai Qian, Zhang Zhigang, et al. Power quality[M]. Beijing: Tsinghua University Press, 2006: 11-14.(in Chinese)
[2] 肖湘宁,徐永海,刘昊.电压凹陷特征量检测算法研究[J].电力自动化备,2002,22(1):19-22.
Xiao Xiangning,Xu Yonghai,Liu Hao.Research on the detection method of voltage sag characteristics[J]. Electric Power Automation Equipment, 2002, 22(1): 19-22.(in Chinese)
[3] 江辉,刘顺桂,尹远兴,等.基于小波和改进S 变换的电能质量扰动分类[J].深圳大学学报理工版,2014,31(1):23-26.
Jiang Hui, Liu Shungui, Yin Yuanxing, et al. Classification of power quality disturbance based on wavelet and improved S-transform[J]. Journal of Shenzhen University Science and Engineering, 2014, 31(1): 23-29.( in Chinese)
[4] Ding Ning, Cai Wei, Suo Juan, et al. Voltage sag disturbance detection based on RMS voltage method[C]// Power and Energy Engineering Conference. Wuhan: IEEE, 2009: 1-4.
[5] 王效孟,周勇,刘继承,等.检测电压暂降特征量的有效值算[J].低压电器,2010(10):48-51.
Wang Xiaomeng, Zhou Yong, Liu Jicheng, et al. Detection method of voltage sages characterizations using RMS algorithm[J].Low Voltage Apparatus, 2010(10):48-51.(in Chinese)
[6] 秦英林,田立军.短时电压扰动检测与定位新方法[J].电力系统保护与控制,2010,38(4):21-24.
Qin Yinglin, Tian Lijun. A new method to detect and locate instantaneous voltage disturbances[J]. Power System Protection and Control, 2010, 38(4): 21-24.(in Chinese)
[7] 侯世英,刘早晨,嵇丽明,等.单相电压骤降特征量的求导检测算法[J].电网技术,2009,33(14):52-55.
Hou Shiying, Liu Zaochen, Ji Liming. A derivation algorithm to detect characteristic quantity of single phase voltage sag[J].Power System Technology, 2009, 33(14): 52-55.(in Chinese)
[8] Singh S K, Goswami A K, Sinha N. Power system harmonic parameter estimation using bilinear recursive least square (BRLS) algorithm[J]. International Journal of Electrical Power and Energy Systems, 2015, 67:1-10.
[9] 任文琳,赵庆生,何志方.基于卡尔曼滤波的电压扰动检测算[J].水电能源科学,2012,30(11):198-200.
Ren Wenlin, Zhao Qingsheng, He Zhifang. Detection of voltage disturbance based on Kalman filter algorithm[J].Water Resources and Power, 2012, 30(11): 198-200.(in Chinese)
[10] 闵伟,周志宇,周振华.改进型Sage-Husa卡尔曼滤波器在电压暂降检测中的应用[J].电网技术,2013,37(1):230-234.
Min Wei, Zhou Zhiyu, Zhou Zhenhua. Application of improved Sage-Husa Kalman filter in voltage sag detection[J]. Power System Technology, 2013, 37(1): 230-234.(in Chinese)
[11] 于静文,薛蕙,温渤婴.基于卡尔曼滤波的电能质量分析方法综述[J].电网技术,2010,34(2):97-103.
Yu Jingwen, Xue Hui, Wen Boying. A survey on Kalman filtering based methods for power quality analysis[J].Power System Technology,2010,34(2):97-103.(in Chinese)
[12] Routray A, Pradhan A K, Rao K P. A novel Kalman filter for frequency estimation of distorted signals in power systems[J]. IEEE Transactions on Instrumentation and Measurement, 2002, 51(3): 469-479.
[13] Reza M S, Ciobotaru M, Agelidis V G, et al. Instantaneous power quality analysis using frequency adaptive Kalman filter technique[C]// The 7th International Power Electronics and Motion Control Conference. Harbin, China: IEEE, 2012: 81-87.
[14] Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE, 2004, 92(3): 401-422.
[15] 江辉,谢兴,王志忠,等.基于优化无迹Kalman滤波的电网动态谐波估计[J].深圳大学学报理工版,2015,32(2):188-195.
Jiang Hui, Xie Xing, Wang Zhizhong, et al. Dynamic harmonic estimation based on optimized unscented Kalman filter model[J]. Journal of Shenzhen University Science and Engineering, 2015, 32(2): 188-195.(in Chinese)
[16] 王法胜,鲁明羽,赵清杰,等.粒子滤波算法[J].计算机学报,2014,37(8):1679-1694.
Wang Fasheng, Lu Mingyu, Zhao Qingjie, et al. Particle filtering algorithm[J].Chinese Journal of Computer, 2014, 37(8): 1679-1694.(in Chinese)
[17] 陈菲琪,吴晓丹.基于粒子滤波的多目标跟踪研究[J].计算机仿真,2010,27(6):147-150.
Chen Feiqi, Wu Xiaodan. Multiple targets tracking research based on particle filter[J]. Computer Simulation,2010, 27(6): 147-150.(in Chinese)
[18] 李雁斌,曹作良,刘常杰,等.基于粒子滤波的全方位视觉传感器实现移动机器人导航[J].传感技术学报,2009,22(5):745-750.
Li Yanbing, Cao Zuoliang, Liu Changjie, et al. Omani directional visual senor for mobile robot navigation based on prticle filter[J]. Chinese Journal of Sensors and Actuators, 2009, 22(5): 745-750.(in Chinese)
[19] López R A,Yuz J I, Creixell W U, et al.Recursive parameter and state estimation for a mining industry process[C]// The 20th Mediterranean Conference on Control & Automation (MED). Barcelona, Spain: IEEE, 2012: 30-35.
[20] Ray P K, Subudhi B. Ensemble Kalman filter based power system harmonic estimation[J].IEEE Transactions on instrumentation and measurement, 2012, 61(12): 3216-3124.
[21] 胡士强,敬忠良.粒子滤波原理及其应用[M].北京:科学出版社,2010.
Hu Shiqiang, Jing Zhongliang. Theory and application of particle filter[M]. Beijing:Science Press, 2010.(in Chinese)
[22] Tian Lei, Rong Jian, Zhong Xiaochun, et al. UPF algorithm and its application in the GPS/INS integrated navigation[C]// International Conference on Wireless Communications and Signal Processing. Nanjing, China: IEEE, 2009: 1-4.
[23] 汲清波,冯池,吕晓凤.UKF、PF与UPF跟踪性能的比较[J].计算机工程与应用,2008,44(32):60-63.
Ji Qingbo, Feng Chi, Lv(Lyu) Xiaofeng. Comparing of target tracking performances of UKF,PF and UPF[J]. Computer Engineering and Applications, 2008, 44(32): 60-63.(in Chinese)
【中文责编:英子;英文责编:雨辰】
Estimation of dynamic harmonics in power systems
based on unscented particle filter
Jiang Hui1†, Chen Li1, Shuai Shiqi1, and Peng Jianchun2
1)College of Optoelectronic Engineering, Shenzhen University, Shenzhen 518060, Guangdong Province, P.R.China
2) College of Mechatronics and Control Engineering, Shenzhen University, Shenzhen 518060, Guangdong Province, P.R.China
Abstract:This paper proposes a new method for estimating dynamic harmonics in power systems based on the unscented particle filter (UPF) algorithm. The UPF algorithm is used to estimate the values and covariance of the state variables of the dynamic harmonics in power systems. These estimated values are used to generate the importance density function of particle filter (PF) algorithm. The optimal estimation of dynamic harmonics in the power system is achieved by using the derived PF algorithm. The proposed method overcomes not only the restriction of Gaussian distribution noise required in unscented Kalman filters (UKF) but also the drawback of easy degeneration for conventional PF. In addition, it retains the high performance of UKF in processing nonlinearity and the strong anti-interference capability of PF.Experiments show that the estimates of dynamic harmonic amplitude and phase by the proposed method are closer to the true values under both Gaussian noise and non-Gaussian noise situations.
Key words:power system; power quality; dynamic harmonic estimation; particle filter; unscented Kalman filter; unscented particle filter
作者简介:江辉(1968—),女,深圳大学教授.研究方向:智能电网、电能质量分析与控制.E-mail:huijiang@szu.edu.cn
基金项目:国家自然科学基金资助项目(51477104);深圳市基础研究计划资助项目(JCYJ20140418193546100)
中图分类号:TM 711;TM 93
文献标志码:A
doi:10.3724/SP.J.1249.2016.01080

