考虑换流器控制特性的交直流混联微电网状态估计

陈和升，卫志农，孙国强，陈胜，臧海祥

(河海大学能源与电气学院， 南京市 210098)

考虑换流器控制特性的交直流混联微电网状态估计

陈和升，卫志农，孙国强，陈胜，臧海祥

(河海大学能源与电气学院， 南京市 210098)

交直流混联微电网是分布式发电(distributed generation, DG)装置并网的良好解决方式，因此，含DG的交直流混联微电网状态估计研究具有现实意义。针对换流器控制特性多样化及直流网络接入，该文提出适用于多种运行模式的交直流混联微电网状态估计模型。首先，针对微电网的孤岛运行特性，建立DG的Droop型节点模型。接着，根据交直流混联微电网状态估计的特点，配置相应的伪量测，以提高系统可观测性；同时采用了支路电流幅值量测转换法，以减少雅可比矩阵的求解难度。最后，采用最小二乘估计求解所提出的交直流混联微电网状态估计模型。通过IEEE13节点算例进行验证，结果表明，所提模型能够适用于并网和孤岛两种运行方式，具有良好的工程实用价值。

微电网；换流器；伪量测；分布式电源(DG)；状态估计

0 引 言

具有经济和环保双重优势的分布式发电技术正日趋成熟，因而电网中分布式发电(distributed generation, DG)装置的数目在不断增加[1-4]。另外，目前大部分用户侧负载、可再生能源发电以及储能装置都是采用直流方式进行并网，建立直流微电网可减少电力变换环节，且具有提高电能利用率等优势[5-7]。但由于传统交流输电网的长久发展，直流网络不可能完全取代现有交流网络。为此，交直流混联微电网作为DG并网以及连接AC-DC网络的良好解决方案，已成为当前电力行业的研究热点和发展趋势[8-10]。

状态估计的核心功能是过滤冗余量测数据，从而为能量管理系统(energy management system, EMS)提供一系列可信估计值[11]。针对具有多种运行状态的交直流混联微电网的状态估计问题，目前国内外已有一些研究工作。文献[12]采用基于支路电流的状态估计算法，将DG分为可控和不可控两种类型，但文中并没有考虑DG并网时换流器如何建模。文献[13]提出一种微电网状态估计模型，可以实现网络结构辨识和孤岛运行状态估计。文献[14]研究了多类型DG的主动配电网分布式三相状态估计，建立了DG并网的三相模型，解决了DG三相不对称注入功率问题。文献[15]将支路电流作为状态量，并且将功率量测量转化为等效支路电流，拓展为三相配电网状态估计。文献[16]提出了微电网在孤岛运行时，网络中DG采用分散下垂控制方式，建立其在潮流计算中的平衡方程。文献[17]则提出交直流混联微电网这一概念，并给出交直流混联微电网连接点在潮流计算中的处理方式，但由于采用单相来描述系统，无法准确体现系统的三相特性。综上可见，现有的交直流混联微电网状态估计算法，大部分来源于配电网状态估计算法[18-19]，缺乏对以下几点因素的考虑：(1)交直流混联微电网运行方式(并网/孤岛)；(2)孤岛运行时系统中没有平衡节点；(3)系统频率作为各DG联系变量；(4)换流器并网节点控制特性。

本文针对具有多种运行状态的交直流混联微电网，提出基于加权最小二乘法(weighted least square, WLS)的交直流混联微电网状态估计模型。首先，建立交直流混联微电网中各元件的稳态模型，将DG运行状态加到状态估计的状态变量中，并配置相应的伪量测以保证状态估计的可观测性；其次，鉴于支路电流幅值与三相节点电压之间复杂的非线性函数关系，提出一种基于支路功率的量测转换方法，简化了雅可比矩阵的计算；最后，采用以IEEE13节点为基础建立的交直流混联微电网算例，测试微电网并网与孤岛两种运行方式，验证所提方法的有效性和适用性。

1 交直流混联微电网系统建模

1.1 馈线模型

在交直流混联微电网中，由于三相不平衡问题更加突出，一般采用三相不对称馈线模型，等值回路如图1所示。

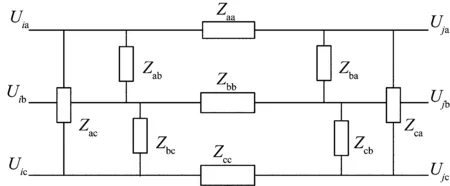
图1 馈线三相模型Fig.1 Three-phase feeder model

对于该模型可建立a-b-c三相的3×3阻抗矩阵，该矩阵联系了三相节点电压和三相支路电流：

(1)

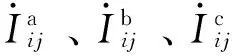
1.2 负荷模型

在稳态条件下，负荷功率与系统电压及系统频率之间的非线性函数关系称为负荷的静态模型。本文将系统频率设置为状态变量，负荷的静态模型需计及系统频率偏差影响，多项式模型[20]如下：

(2)

(3)

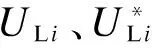
1.3 换流器稳态模型

换流器是由单个或多个换流桥组成的进行交、直流转换的设备。大部分DG以及直流微电网都需经过换流器的转换才能并入交流电网。考虑到目前电压源型换流器在DG并网换流器中比较主流，本节以图2为例首先介绍PWM(pulse width modulation)换流器稳态模型[21]。

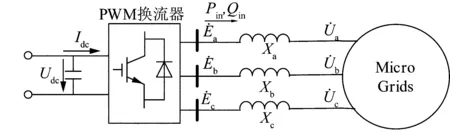
图2 PWM换流器并网Fig.2 Integration of PWM inverter

对于PWM换流器作如下假设：

(1)换流器本身结构及输出电压三相对称；

(2)不考虑换流器本身的损耗。

换流器两侧必须满足功率平衡及电压约束条件：

Pin,ac=Pin,dc

(4)

(5)

式中：Pin,ac、Pin,dc分别为PWM换流器交流侧三相注入总有功功率和直流侧注入有功功率；Eac为PWM换流器出口线电压幅值；M为幅度调制比，一般为0～1之间的数；Udc为PWM换流器直流侧接口电压值。

对于该换流器节点，一般可以通过控制其两侧状态变量，达到所设定的运行要求。因此，在状态估计过程中可根据控制的具体状态变量，将其分为不同的节点类型，本文主要介绍其中2种。

(1)P-Q节点，即其控制目标为三相注入总功率恒定，光伏系统及燃料电池等DG大多采用此方式实现并网。

(2)Udc-Q节点，即其控制目标为直流侧电压和交流测三相注入总无功功率恒定，直流微电网可通过此方式接入交流微电网中，实现直流单相到交流三相的转变。

而孤岛运行时，DG作为电源，不仅要满足负荷的需求，同时还负责系统电压与频率的控制。此时由于没有平衡节点，所有DG单元不能简单处理为PV或PQ节点。因此，在孤岛运行时，需加一类DG节点：Droop节点[16]。

图3 Droop节点Fig.3 Droop node

Droop控制下的DG一般通过SPWM(sinusoidal pulse width modulation)换流器并网，其静态模型如图3所示。在该模型中，DG通过自身输出的有功功率和无功功率的量测值，利用相关Droop特性(P-f/Q-U)确定输出电压幅值和频率的参考值，进而控制其输出功率。在Droop控制下，DG的P-f表达式[22]为

(6)

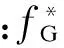
从式中可以看出，其下垂特性保证了网络孤岛运行时系统频率稳定。另一方面，该DG的Q-U表达式为:

(7)

Uoq=0

(8)

根据式(7)-(8)，输出电压向量分别投影到d轴和q轴上，并且q轴分量设置为0。连接在节点i上的DG，通过派克逆变换可得到三相输出电压表达式：

(9)

由式(9)可知，在Droop控制下此类节点同样满足换流器输出电压三相对称的假设。

节点i的DG静态下垂增益mPi、nQi根据电压和频率约束条件计算得到:

(10)

(11)

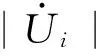
(12)

(13)

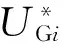
2 交直流混联微电网状态估计模型

2.1 加权最小二乘估计

在较低的量测冗余度下，WLS估计是配网侧/微网侧最为高效的估计器[11]。根据其定义，可建立目标函数如下：

J(x)=[z-h(x)]TW[z-h(x)]

(14)

式中：z为量测量；x为状态量；h(x)描述量测量与状态量之间的非线性关系；W为量测权重矩阵。

为求解式(14)最小值，先将非线性函数h(x)进行泰勒展开，并忽略二次以上的高阶项，可得如下迭代方程：

(15)

(16)

2.2 基于WLS的交直流混联微电网状态估计模型

与传统配电网类似，在交直流混联微电网状态估计中，量测量包括多种类型：节点电压幅值量测、负荷功率量测、支路功率量测以及支路电流幅值量测。由于状态变量为三相电压向量，而DG并网侧的量测量(已知量)为三相总功率(即单相变量)，为保证状态估计的可观测性，需根据换流器的控制特性增加相应的伪量测。对于交直流混联微电网连接处，由换流器实现交流电网三相到直流电网单相的转变，需满足两侧功率平衡约束条件，同时为其配置相应的伪量测，进一步增加系统量测冗余。

2.2.1 经PWM换流器并网

此时，PWM换流器两侧的状态变量可作为DG并网点的伪量测，从而保证该点的可观测性。

(1)P-Q控制，此时伪量测为三相注入总功率P和Q及该点计及系统频率偏差影响的每相负荷值，则其对应的伪量测方程为：

(17)

(18)

(19)

(20)

式中：左侧用m标记的为相对应的量测量；PLi、QLi表示节点负荷值；PGi、QGi为DG注入功率。

根据换流器输出电压三相对称的特性假设，可得相应的伪量测方程：

(21)

(22)

(23)

(24)

该点相应状态变量的选取：

(25)

对于每个DG并网点，12个未知量，12个方程，可观测。伪量测方程(21)—(24)从理论上严格成立，故设置较大的权重值。

(2)Udc-Q控制，即控制直流侧电压和交流侧无功功率为设定值。此时换流器输出特性与上节的P-Q控制相同。本文设定以此控制策略连接交直流网络，换流器两侧必须满足有功功率平衡约束条件，添加伪量测方程如下：

(26)

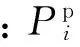
2.2.2 经SPWM换流器并网(Droop节点)

交直流混联微电网处于孤岛运行时，Droop控制下的DG为整个网络供电，以维持系统频率及电压稳定。SPWM换流器输出特性与上节PWM换流器相同，不同的是通过Droop控制特性可得到如下伪量测方程，将系统频率也作为状态变量，以监测孤网运行下的系统频率。

(27)

(28)

2.2.3 支路电流幅值的量测方程处理

在交直流混联微电网中将原来的单相拓展到三相，相应的支路电流幅值可表示为如下矩阵形式:

(29)

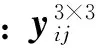
(30)

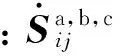
(31)

(32)

(33)

此时支路电流幅值对电压幅值和相角状态变量求偏导，转化为相应的支路功率求偏导，如式(33)所示，此处理大幅减少雅可比矩阵求解的复杂度。

2.2.4 直流微电网

直流微电网[17]与单相处理的传统输电网类似，但由于采用直流形式，状态变量选取各个节点电压幅值，相应的量测配置以负荷功率和支路电流幅值量测为主。

(34)

(35)

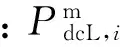
3 算法流程

本文针对具有多种运行状态的交直流混联微电网，提出了基于WLS的交直流混联微电网状态估计算法，实现的基本步骤如下:

(1) 输入网络参数和相应的量测数据；

(2) 初始化状态变量并置迭代次数l=0，

(3) 由各状态变量计算不同量测量的计算值h(x(l))和雅可比矩阵H(x(l))；

(4) 由式(15)、(16)求解修正量并对相应的状态变量进行修正；

(6) 分类输出状态估计结果。

4 算例分析

4.1 仿真系统

本节采用以IEEE13节点为基础建立的交直流混联微电网算例进行分析，如图4所示。原始配电网算例IEEE13节点系统详细参数见文献[24]及附录表A1，考虑在2、3、7和13接入不同控制策略的DG，同时在节点14-15之间通过换流器连接直流微电网。所接入的直流微电网线路和负荷参数见附录表A2和表A3。

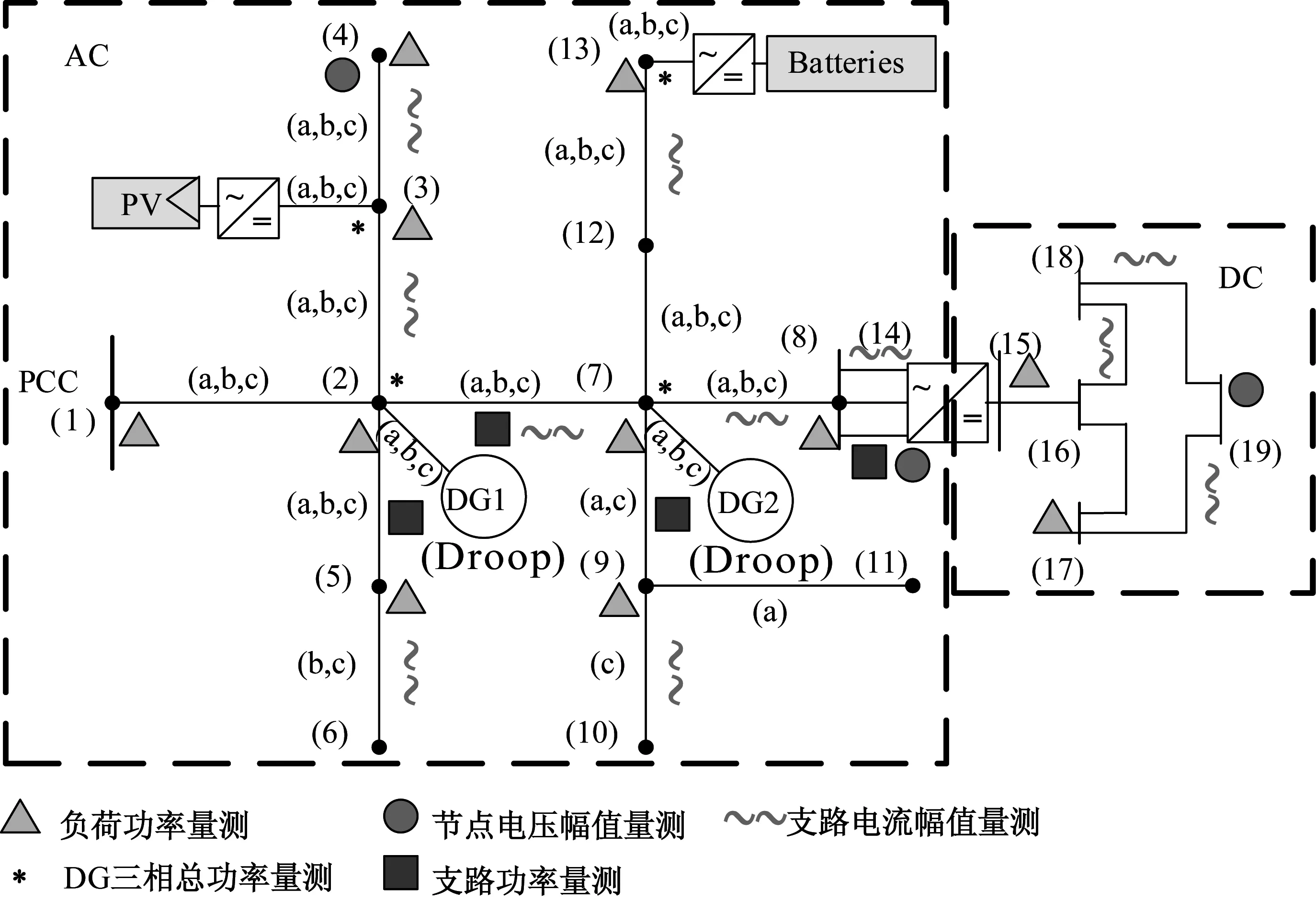
图4 交直流混联微电网Fig.4 AC-DC hybrid microgrid

关于交直流混联微电网状态估计系统量测配置问题，已在图4中详细标注。本文对整个算例采用牛顿拉夫逊法求解潮流，在潮流真值的基础上添加服从正态分布的随机误差：(1)负荷功率量测及DG三相总功率量测是基于历史数据、天气情况等因素预测的伪量测，量测最大误差设置为20%；(2)节点电压幅值、支路电流幅值以及支路功率量测是实时量测，量测最大误差设置为1%。

4.2 结果与分析

4.2.1 并网方式运行

上述系统以并网方式运行，即根节点与公共联接点(the point of common coupling, PCC)相连接，系统中取根节点为平衡节点，系统频率由根节点来维持。此时不计及负荷的电压及频率特性，即假定负荷功率恒定。在并网运行时，DG采用恒功率控制(PQ节点)，不考虑Droop特性。整个网络的其他架构不变，相应的换流器装置详细参数见表1。

表1 换流器控制参数
Table 1 Control parameters of inverter

采用本文所提出的状态估计模型对并网运行的交直流混联微电网进行状态估计，收敛精度为1×10-5的情况下，平均迭代4次收敛，选取其中一种结果来说明估计效果。此时节点电压幅值的最大估计误差和平均估计误差的标幺值分别为5.26×10-3和9.74×10-4，直流微电网和换流器三相输出电压估计效果见图5和表2。

图5 直流微电网节点电压估计结果比较Fig.5 Comparison of estimated and actual values for DC microgrid voltage

由以上估计效果可知，对于并网型交直流混联微电网，本文所提出的状态估计模型有效。

4.2.2 孤岛方式运行

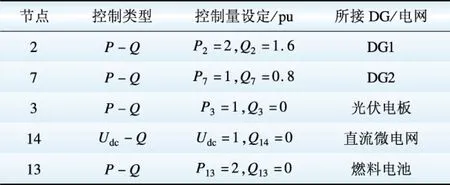
上述系统以孤岛方式运行，即根节点与PCC节点断开，取节点1的a相电压相角为参考相角。正常运行时系统的基准容量取1 MW，系统基准频率取50 Hz。节点2、7上的DG通过Droop控制方式来担当主电源为整个微电网供电, 其具体参数(标幺值)如表3所示。同时节点3、13及14通过PWM换流器接入不同DG及直流微电网，控制策略和详细参数见表4。

同样采用本文所提出的状态估计模型对孤岛运行的交直流混联微电网进行状态估计，收敛精度为1×10-5的情况下，平均迭代6次收敛，选取其中一种结果来说明估计效果。

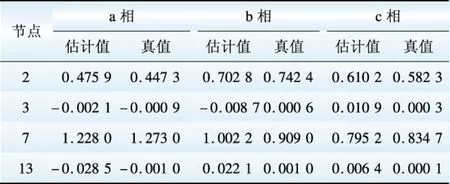
表5与表6为DG每相有功功率和无功功率估计结果。由表5-6可知，通过本文算法可根据三相总功率伪量测估计出微电网中处于不同控制策略下DG每相功率的输出情况。由于系统的三相不平衡性，各DG三相功率的输出估计值并不是完全相等，甚至出现严重不平衡的情况。

表2 换流器三相输出电压估计结果
Table 2 Comparison of estimated and actual values for inverter three-phase output voltage

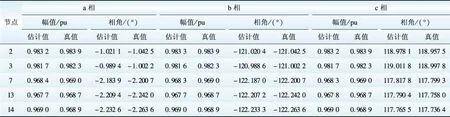
表3 Droop节点控制参数Table 3 Control parameters of Droop node

表4 换流器控制参数Table 4 Control parameters of inverter

表5 DG每相有功功率估计结果Table 5 Comparison of estimated and actual values for injected active power of per phase of DG

pu

表6 DG每相无功功率估计结果Table 6 Comparrison of estimated and actual values for injected reactive power of per phase of DG

pu

而由图6、7的三相注入总功率比较结果可知，处于Droop控制下的DG1与DG2承担着整个交直流混联微电网的大部分负荷，起到了在孤岛运行时主电源的作用。同时也能够从图中看出三相注入功率估计值之和与输出三相总功率的潮流真值比较效果，其有功功率的最大估计误差和平均估计误差的标幺值分别为0.030 1和0.014 1，充分说明了本文状态估计模型能够较准确地反映出交直流混联微电网孤岛运行时不同DG的运行情况。

由表7中结果比较可知，换流器并网处的输出电压的估计值由于伪量测的条件约束，表现出三相对称这一输出特性，与假设条件相一致。同时得到了比较准确的直流微电网的运行状态及系统频率估计值49.953 6 Hz(真值49.960 0 Hz)。

由以上估计效果可知，交直流混联微电网孤岛运行时，本文所提出的状态估计模型同样有效。

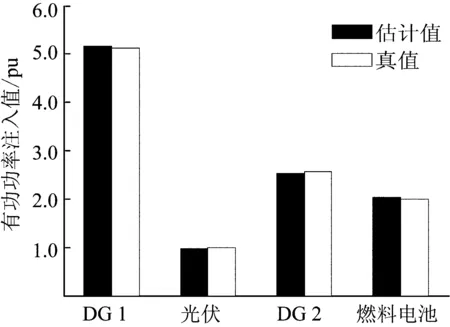
图6 DG总有功输出Fig.6 Comparison of total active power output of DG

图7 DG总无功输出 Fig.7 Comparison of total reactive power output of DG

5 结 论

(1)本文提出的模型兼顾交直流混联微电网的三相不平衡以及直流微电网接入等多种运行状态组合情况，有良好的工程实用价值。

(2)分散下垂控制的孤岛微电网中无平衡节点，DG通过换流器控制实现三相并网。为此，本文针对其不同的控制特性，并考虑注入功率三相不对称性，进行相应的伪量测配置，最终保证系统可观测。

(3)支路电流幅值量测转换可有效解决状态估计中，三相支路电流幅值与节点电压之间的非线性函数复杂关系问题，简化求解过程，为状态估计算法提供新的研究思路。

表7 系统节点三相电压估计结果
Table 7 Comparison of estimated and actual values for system node

[1]王成山．微电网分析与仿真理论[M]．北京：科学出版社，2013：1-11．

[2]王成山，王丹，周越．智能配电系统架构分析及技术挑战[J]．电力系统自动化，2015，39(9)：1-8． WANG Chengshan，WANG Dan，ZHOU Yue，et al．Framework analysis and technical challenges to smart distribution system[J]．Automation of Electric Power Systems，2015，39(9)：1-8．

[3]刘杨华，吴政球，涂有庆，等．分布式发电及其并网技术综述[J]． 电网技术，2008，32(15)：71-76． LIU Yanghua，WU Zhengqiu，TU Youqing，et，al．A survey on distributed generation and its networking technology[J]．Power System Technology，2008，32(15)：71-76．

[4]郑漳华，艾芊．微电网的研究现状及在我国的应用前景[J]．电网技术，2008，32(16)：27-31． ZHENG Zhanghua，AI Qian．Present situation of research on microgrid and its application prospects in China [J]．Power System Technology，2008，32(16)：27-31．

[5]KWASINSKI A．Quantitative evaluation of DC microgrids availability：Effects of system architecture and converter topology design choices[J]． IEEE Transactions on Power Electronics，2011，26(3)：835-851．

[6]刘家赢，韩肖清，王磊，等．直流微电网运行控制策略[J]．电网技术，2014，38(9)：2356-2362． LIU Jiaying，HAN Xiaoqing，WANG Lei，el al．Operation and control strategy of DC microgrid[J]．Power System Technology，2014，38(9)：2356-2362．

[7]ELSAYED A T, MOHAMED A A, MOHAMMED O A． DC microgrids and distribution systems：An overview[J]．Electric Power Systems Research，2015(119)：407-417．

[8]GUERRERO J M，LOH P C，LEE T L，et al．Advanced control architectures for intelligent microgrids-part II：power quality，energy storage，and AC/DC microgrids[J]．IEEE Transactions on Industrial Electronics，2013，60(4)：1263-1270．

[9]LOH P C，LI D，CHAI Y K，et al．Autonomous operation of ac-dc microgrids with minimised interlinking energy flow[J]．IET Power Electronics，2013，6(8)：1650-1657．

[10]HUANG Y F，WERNER S，HUANG J，et al．State estimation in electric power grids：meeting new challenges presented by the requirements of the future grid[J]．Signal Processing Magazine，IEEE，2012，29(5)：33-43．

[11]于尔铿．电力系统状态估计[M]．北京：水利电力出版社，1985．

[12]LU J，ZHU G，MIAO Y．State estimation of the micro-grid[M]． New York: Springer Verlag New York Inc，2014：517-527．

[13]KORRES G N，HATZIARGYRIOU N D，KATSIKAS P J．State estimation in multi-microgrids[J]．European Transactions on Electrical Power，2011，21(2)：1178-1199．

[14]卫志农，陈胜，孙国强，等．含多类型分布式电源的主动配电网分布式三相状态估计[J]．电力系统自动化，2015，39(9)：68-74． WEI Zhinong，CHEN Sheng，SUN Guoqiang，et al．Distributed three-phase state estimation for active distribution network integrated with different types of distributed generators[J]．Automation of Electric Power Systems，2015，39(9)：68-74．

[15]BARAN M E，KELLEY A W．State estimation for real-time monitoring of distribution systems[J]．IEEE Transactions on Power Systems， 1994，9(3)：1601-1609．

[16]ABDELAZIZ M M，FARAG H E，EL-SAADANY E F，et al．A novel and generalized three-phase power flow algorithm for islanded microgrids using a newton trust region method[J]．IEEE Transactions on Power Systems， 2013，28(1)：190-201．

[17]LI C，CHAUDHARY S K，VASQUEZ J C，et al．Power flow analysis for droop on trolled LV hybrid AC-DC microgrids with virtual impedance[C]//PES General Meeting Conference & Exposition，IEEE，2014：1-4．

[18]董树锋，何光宇，王雅婷，等．配电网状态估计研究综述[J]．华东电力，2013，41(8)：1586-1591． DONG Shufeng，HE Guangyu,WANG Yating，et al．A research survey on distribution network state estimation[J]．East China Electric Power，2013，41(8)：1586-1591．

[19]高赐威，孔峰，陈昆蔽．一种配电网状态估计实用算法的探讨[J]．电网技术，2003，27(2)：80-83． GAO Ciwei，KONG Feng，CHEN Kunwei．A novel and practical state estimation algorithm for power distrbution network with complicated structure[J]．Power System Technology，2003，27(2)：80-83．

[20]李春，卫志农，孙国强，等．考虑风力发电波动引起频率偏差的电力系统状态估计[J]．电网技术，2015，39(5)：1301-1306． LI Chun，WEI Zhinong，SUN Guoqiang，et al．State estimation of power system considering frequency deviation caused by fluctuation of wind power generation[J]．Power System Technology，2015，39(5)：1301-1306．

[21]王成山，孙充勃，彭克，等．微电网交直流混合潮流算法研究[J]．中国电机工程学报，2013，33(4)：8-15．WANG Chengshan，SUN Chongbo，PENG Ke，et al．Study on AC-DC hybrid power flow algorithm for microgrid[J]．Proceedings of CSEE，2013，33(4)：8-15．

[22]ROKROK E，GOLSHAN M E H．Adaptive voltage droop scheme for voltage source converters in an islanded multibus microgrid[J]．IET Generation，Transmission & Distribution，2010，4(5)：562-578．

[23]POGAKU N，PRODANOVI M，GREEN T C．Modeling，analysis and testing of autonomous operation of an inverter-based microgrid[J]． IEEE Transactions on Power Electronics，2007，22(2)：613-625．

[24]KERSTING W H． Radial distribution test feeders[C]//Power Engineering Society Winter Meeting. IEEE，2001(2)：908-912．

(编辑 张小飞)

附录A

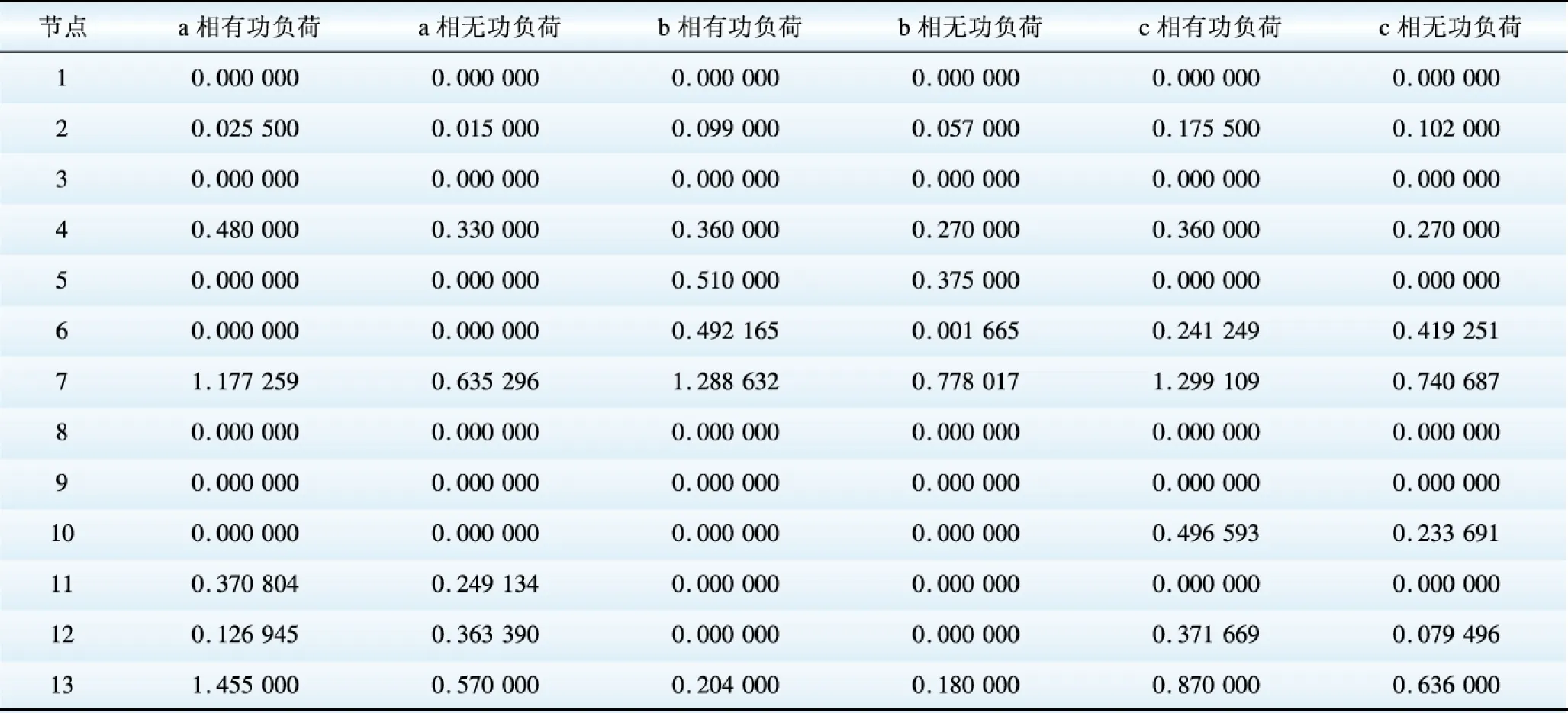
表A1 IEEE 13节点系统节点负荷
Table A1 Loads of IEEE 13 system pu

State Estimation of AC-DC Hybrid Microgrid Considering Inverter Control Characteristics

CHEN Hesheng, WEI Zhinong, SUN Guoqiang, CHEN Sheng, ZANG Haixiang

(College of Energy and Electrical Engineering, Hohai University, Nanjing 210098, China)

The AC-DC hybrid microgrid is the good solution for distributed generation (DG) paralleling in grid. Therefore, it is of great value to study the state estimation of AC-DC hybrid microgrid with DG. According to the control characteristic diversification of inverter and the integration of DC grid, this paper proposes a novel state estimation algorithm for the AC-DC hybrid microgrid considering operating status. Firstly, we establish the Droop-type node model of DG based on the islanded operating characteristics of microgrid. Furthermore, we formulate the appropriate pseudo-measurements to improve the system observability, according to the state estimation features of the AC-DC hybrid microgrid. Meanwhile, we use the branch current amplitude measurement conversion to reduce the difficulty of solving Jacobian matrix. Finally, we adopt the least square estimation to solve the proposed state estimation model of the AC-DC hybrid microgrid. The proposed models on grid-connected and islanded operation modes are tested on the modified IEEE-13 bus distribution system, whose results demonstrate the effectiveness of the proposed model in engineering applications.

microgrid; inverter; pseudo-measurements; distributed generation (DG); state estimation

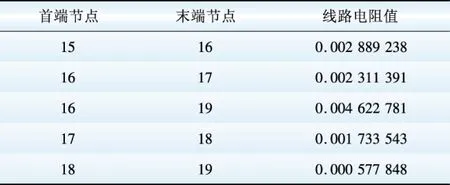
表A2 直流网络线路电阻值Table A2 Line resistance values of DC grid pu

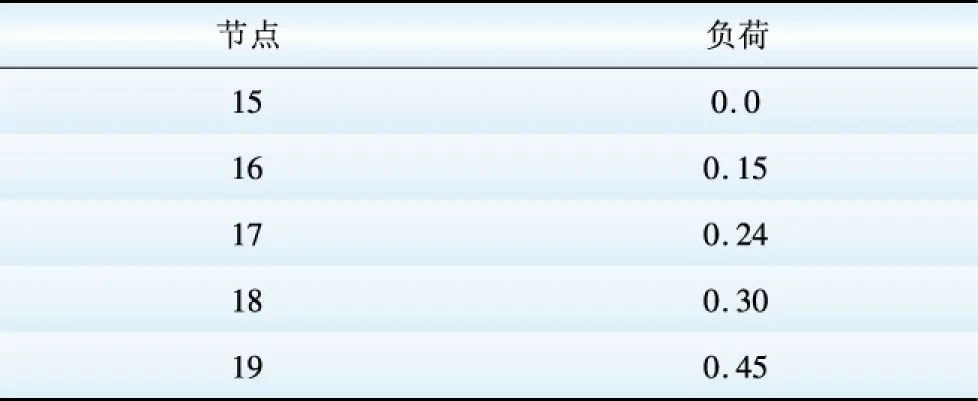
表A3 直流网络节点负荷Table A3 Loads of DC grid pu

国家自然科学基金项目(51107032，61104045，51277052)

TM 727

A

1000-7229(2016)05-0091-09

10.3969/j.issn.1000-7229.2016.05.016

2015-12-25

陈和升(1990)，男，硕士，研究方向为电力系统状态估计；

卫志农(1962)，男，博士，教授，博士生导师，研究方向为电力系统运行分析与控制、输配电系统自动化等；

孙国强(1978)，男，博士，副教授，研究生导师，研究方向为电力系统运行分析与控制；

陈胜(1990)，男，硕士，研究方向为电力系统状态估计与优化运行;

臧海祥(1986)，男，博士，讲师，研究方向为电力系统规划与运行，新能源发电技术。

Project supported by National Natural Science Foundation of China (51107032, 61104045, 51277052)