归纳推理思维在小学数学教学中的应用

杨清山

（大庆市三永学校 黑龙江大庆 163711）

归纳推理思维在小学数学教学中的应用

杨清山

（大庆市三永学校 黑龙江大庆 163711）

在全面素质教育的时代要求下，2001年教育部制订并实施了《全日制义务教育数学课程标准（实验稿）》（以下简称《标准》）。《标准》以详实、具体的语言对小学阶段数学的归纳推理能力做出了要求。

《标准》对小学阶段的学生数学学习总体内容和目标提出要求，及现实的、有意义的、具有挑战性的，要有利于观察、实验、猜想、论证、推理与交流等数学活动。具体到归纳推理部分，《标准》要求：经历观察、实验、猜想、证明等数学基本思维过程后，学生可以做出简单的演绎推理和有条理的表达自己的观点。可以看出归纳推理部分已经作为小学数学教学过程的一个重点，并要求以潜移默化的方式将归纳推理思维渗透到日常教学中。针对小学生个体的差异性和层次性需要，我们来探讨一下如何在实际教学过程中实现归纳推理思维训练。[1]

一、归纳推理的内涵

归纳推理是指由个别的事物或现象推出该类事物或现象的普遍性规律的推理。归纳推理与演绎推理相对，但在归纳方向上还要借助到演绎推理的思维，具体来看就是通过观察、分析、抽象、比较、概括、反证等过程方法对生活中个例性的事物进行探讨、描述，最后得出一个普适性的规律，从哲学范畴来看是一种共性寄宿于个性之中的阐释。这种思维（方法）在自然科学的发展过程中具有重要地位，特别是对于数学学科来说尤为鲜明。[2]

二、归纳推理的分类及应用

1．完全归纳推理

完全归纳推理是根据一个群体中的所有个体的某一特性推断出这一群体都具有该类特性的推理。完全归纳推理表面看来一种无实际意义或等同于废话的推理方式，但是在数学教学过程中，特别是小学数学教学过程中具有重要作用。首先是认知作用，根据完全归纳集合内所有个体的特性使孩子们的对集合的整体属性的认识从个体上升到一般；其次是论证作用，由于完全归纳推理的个体特性与集合属性之间的必然性联系，能让小学第一、二学段的孩子们的脑中产生强有力的知识点论证过程。以小学六年级数学（下）——北师大版为例。[3]

“相”在棋盘上走“田”字。问：“相”能走到（0，2）、（3，4）的位置吗？具体路线是什么？你发现了什么？（此题也可换为“马”可以到哪个位置？）

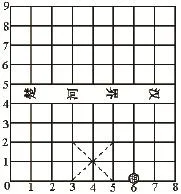
这道趣味题目在训练孩子们推理能力的时候就应该用到完全归纳推理的思维，让学生们尝试所有可能来挪动“相”，最后发现相可以走到7个位置，可以走到（0，2），不可以走到（3，4）。规律是每个点的“数对”中两个数都是偶数，每个点的“数对”的和相等或是相差4的倍数。（如果换成是“马”走“日”字，可以走到任何位置）。

这类完全归纳思维的题目从小学低年级的飞行棋、跳棋类题目（包括小学奥数训练）开始就应该在教学过程中加以渗透。

2．不完全归纳推理

不完全归纳推理指的是根据某一类事物中的部分个体属性推论出该类事物整体都具有某种属性或特点。在实际教学过程中部分个体又称实例，整体属性又称为结论。不完全归纳又分为枚举归纳推理和科学归纳推理。根据小学生心理和思维发展程度，枚举归纳推理在小学数学教学和反证过程中占有核心地位，在小学高年级（5、6年级）会接触到少量科学归纳推理，及由具象到抽象的转化，为初中数学的学习最好准备。以小学一年级（下）加一加，说一说，为例。

16+17= 16+26= 16+27=

26+27= 17+27= 17+26= （16、17、26、27）

你发现了什么？你能找到同样规律的另外4个数字吗？

这个题目属于枚举归纳思维的范畴，就是在100个连续数字表内找规律，通过学生的观察和不断尝试（实验），可以找到许多4个数字的集合，这时需要教师的带领学生进行评述和解析，将归纳思维渗透到教学过程中，并以演绎推理进行求证。① 横向两个数的和相差20；② 竖行相邻两数和相差2；③ 斜框两数和相等。通过枚举归纳得到的一般规律，在到80-100数字中寻找4个数字进行求证，让学生从小数字得到的规律也可以应用到大数字范畴。[4]

这个案例在小学一年学段还没有涉及到科学归纳推理思维，但是学生进入3-4年级，我们可以尝试用这样的推理：① 因为每一行是连续的自然数并且每行都是10个数，所以对应上下两行的数字相差10，那么横向相邻两个数的和一定相差20；② 由于是连续自然数，那么相邻横向相邻数相差1，结果纵向两个数的和与相邻的纵行和相差2；③ 由于是连续自然数，所以横向相邻差为1，结果斜框和相等。

归纳推理思维是小学数学教学过程中非常重要的思想，无论对学生认识自然事物，熟悉社会生活，还是对于初、高中数学成绩的提高都具有现实的基础意义。归纳推理思维是数学学科的基础，几乎所有的数学的分支学科都潜移默化中包含了划归思想，所以教材中关于归纳推理的习题、趣味问答还是能力提高试题几乎都可以同时用到枚举归纳推理和科学归纳推理，特别是科学归纳推理是素质教育的一个核心目标，对学生未来从事各行业工作都具有促进作用。

[1]王瑾.小学数学课程中归纳推理的理论与实践研究[D].长春：东北师范大学，2011.

[2]蔡凌燕.小学数学教材中数学思想方法的探究[J].教学与管理，2008.

[3]彭文会.知识背景对归纳推理的影响[J].重庆工商大学学报（自然科学版），2005.

[4]马云鹏.小学数学教学论[M].北京：人民教育出版社，2006.