自平衡机器人中数据融合算法的研究与实现
吕传龙,曹华杰,刘浩东
(1.西南交通大学 电气工程学院,四川 成都 610031;2.西南交通大学 信息科学与技术学院,四川 成都 611756)
自平衡机器人中数据融合算法的研究与实现
吕传龙1,曹华杰2,刘浩东1
(1.西南交通大学 电气工程学院,四川 成都 610031;2.西南交通大学 信息科学与技术学院,四川 成都 611756)
轮式自平衡机器人是一种通用的机器人,它适用于各种复杂环境中,通过陀螺仪和加速度计采集的数据可以控制其平衡性,但是不够精确和实时。为了进一步提高系统的响应,文中通过离散卡尔曼算法将ENC03陀螺仪和MMA7260加速度计采集的数据进行融合输出。首先研究了传统的卡尔曼算法,然后建立了适合自平衡机器人的算法模型,最后介绍了其工程实现。通过实时监测可以看出,在未进行角度融合之前,加速度计计算得出的角度在静态和动态都有着极大的噪声。经过卡尔曼滤波算法融合后的角度平滑稳定,达到了预期效果。
自平衡机器人;加速度计;陀螺仪;卡尔曼算法;数据融合
0 引 言
轮式自平衡机器人是控制科学的一个重要研究平台,同时也是实际应用的重要工具。20世纪90年代,日本开展了平衡机器人的相关研究,为后来的移动平衡机器人学建立了相关研究基础。21世纪初,自平衡机器人得到了越来越多的关注,国外高校逐渐采用其作为先进理论的验证平台,机器人公司也开始将轮式自平衡机器人进行商业化。比如,美国公司赛格威研究开发两轮自平衡代步车,除了已经在个人用户的使用上得到推广外,在机场、高档社区和运动场馆等大型空间内也得到使用。近年来,越来越多的互联网公司加入平衡机器人的开发中,对平衡机器人的推广普及有着深刻影响。
1 传感器数据采集
轮式自平衡机器人的稳定运行建立在正确获得其姿态信息的基础上,通过一定的控制算法驱动电机保持平衡稳定状态。其姿态信息主要是指在静止或者平衡状态下,机器人重心与竖直方向的倾角。机器人姿态的信息需要兼顾其动态特性和静态精度,倾角测量需要满足动态与静态性能指标。静态指标是指在稳定状态下可以长时间正确表示实际观察量;动态指标是指当测量的物理量在高速运动状态下,仍可以快速跟随状态变化,并且具有一定的预测性。为了得到机器人的复合要求的姿态倾角,可以采用陀螺仪的角速度动态特性和加速度计的静态精度相结合的方法[1]。
陀螺仪是一种利用科里奥利力原理,对旋转物体测量其角速度的元件。陀螺仪适应于系统运动时的角速度信息,对其积分可以得到实际运动中的倾角。然而,受到陀螺漂移等因素的影响,产生的微小误差经过积分作用之后,会使测量的角度产生巨大的偏差。因此,应对的主要是陀螺漂移的低频噪声[2]。为此,需要设计滤波电路对陀螺仪输出信号进行滤波,将低频噪声滤除,同时要保证系统高频信号不能达到陀螺仪的共振频率。
加速度计是一种测量重力加速度分量以及运动加速度的元件。对于轮式自平衡机器人,利用加速度计元件测量重力加速度分量,进行反三角函数运算得到机器人重心与竖直方向的夹角,作为机器人车体的倾角。加速度计在运行中易受到平台震动这样的高频噪声的影响。设计中采用飞思卡尔半导体公司出品的加速度计MMA7260。根据公式可以推导出倾角的变化量:
Δu=kgsinθ
(1)
其中,u是加速度计输出电压值;g是重力加速度;θ是车模倾角;k是比例系数。
2 卡尔曼数据算法融合研究
得到机器人的姿态信息是平衡车系统最具挑战的部分之一。陀螺仪和加速度计分别为不同的角度传感器,在该系统中采用双传感器进行角度测量。然而,加速度计容易受到自身器件的噪声、电机噪声以及陀螺仪混叠的影响,而且在高速运动的体系下具有严重的滞后特性;陀螺仪噪声小,但是存在着温度漂移现象,静态性能不足以达到要求。为了保留加速度计的静态性能和陀螺仪的动态性能,使两者优势可以相互结合,文中采用多传感器信息融合算法中的滤波器融合算法[3]。
典型的数据融合算法大致分为两类:一类是从频率域来分辨、消除噪声,不考虑信号及噪声的统计特性,例如互补滤波器[4];另一类是使用状态空间法在时域内设计滤波器,例如卡尔曼滤波器[5]。互补滤波的基本思想是通过不同传感器具有互补作用的特性进行角度融合。对于轮式机器人采用互补滤波的方式进行滤波,需要实时地将时域信息转换到频域空间,在频域中设计针对陀螺仪和加速度计的滤波器,最后进行互补融合。
针对上述所选滤波器进行如下设计:利用高通滤波器抑制陀螺仪积分的漂移,利用低通滤波器滤除加速度计的短时性快速变化的信号,将处理后的数据进行融合以得到小车的实际倾角。最后将加速度滤波和陀螺仪滤波的角度各乘以一个权重,其权重和为1即可[6]。其滤波过程如图1所示。然而在复杂的情况下,滤波器的带宽难以动态选择,这给互补滤波器的设计带来了困难。
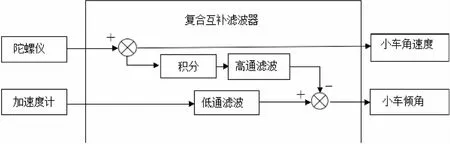
图1 复合互补滤波器
相对于其他滤波方式,卡尔曼滤波有着诸多优点:采用状态空间法设计滤波器,用状态方程表征系统的运动特性,从而避免了在频域中讨论和设计滤波器的繁琐,简单易行[7];在递推运算中,实时量测信息经提炼被浓缩在估计值中,而不必存储时间过程中的量测量[8]。所以,卡尔曼滤波能适用于白噪声激励的任何平稳或非平稳随机向量过程的估计,所得估计在线性估计中精度最佳。
2.1 卡尔曼滤波算法
卡尔曼滤波是一种递推线性最小方差估计,其设计准则与线性最小方差估计相同,估值同样是量测值的线性函数。由于卡尔曼滤波算法使用递推算法,启动时需要给定初始值在内的系统初值。给定的初值在满足一定的条件下,滤波过程中估计可以始终无偏[9]。文献[10]中的算法利用反馈控制来实现对状态的估计,它根据前一时刻的系统状态,估计出当前的系统状态,然后根据当前时刻的实际观测值作为反馈,来修正估计的状态。因此,卡尔曼滤波算法可以分为两个步骤:状态预测和测量修正。状态预测方程由前一刻系统状态和噪声方差预测出当前的系统状态;而测量修正方程则负责修正,在状态预测方程中得到的预测估计状态中加入当前实际传感器的信号,最终得到修正后的系统状态。其滤波算法如图2所示。
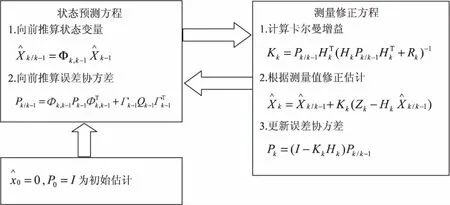
图2 卡尔曼滤波算法
设tk时刻的被估计状态Xk受系统噪声序列Wk-1驱动,对Xk的两侧满足线性关系,若离散线性系统描述为:
(2)
离散型卡尔曼滤波基本方程要满足如下关系[11]:
状态预测方程为:
(3)
测量修正方程为:
(4)
当状态预测方程和测量修正方程循环运算时,就能使输出信号越来越接近真值。使用卡尔曼滤波算法能够有效过滤信号中的噪声。
2.2 自平衡机器人算法模型
根据卡尔曼滤波原理[12],设计滤波算法如下:
以机器人的重心距离竖直方向倾角anglek,陀螺仪的偏差量q_biask,作为状态向量,得到相应的线性系统描述[13]。如公式(5)所示:
(5)
角度预测如下:
angle=angle-q_biask-1*dt+gyro_m*dt=angle+Rate*dt
(6)
方差预测如下:
(7)
角度偏量:
angle_err=incAngle-angle
(8)
滤波增益:
(9)
协方差更新:
(10)
状态估计:
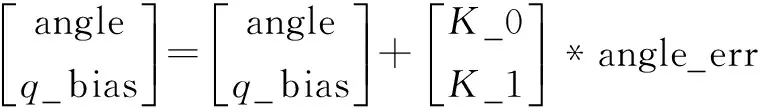
(11)
根据实际情况推导出工程应用算法实现模型,具体的实现方式在下一节介绍。
2.3 卡尔曼融合算法实现
定义函数为KalmanFilter,入口参数为陀螺仪角速度、加速度计。输出参数为滤波角度。该函数主要实现卡尔曼数据融合的过程,计算最优估计角度。函数构造如下:
FloatKalmanFilter(constfloat gyro_m,const float incAngle)
{
定义参数并实现卡尔曼融合算法;
Return angle;
}
定义参数如下:
(1)滤波增益矩阵参数。
floatK_0;floatK_1;floatY_0;floatY_1
(2)去除偏差后的角速度。
floatRate
(3)计算状态预测协方差矩阵的中间矩阵。
floatPdot[4]
(4)定义角度偏量和计算的中间量、下时刻最优估计值角度、陀螺仪的偏差。
floatangle_err;floatE;staticfloatangle=0;staticfloatq_bias=0
(5)定义状态协方差。
staticfloatP[2][2]={{1,0},{0,1}}
(6)卡尔曼状态更新。
angle+=Rate*dt
(7)计算预测协方差矩阵。
Pdot[0]=Q_angle-P[0][1]-P[1][0];
Pdot[1]=-P[1][1];Pdot[2]=-P[1][1];
Pdot[3]=Q_gyro;P[0][0]+=Pdot[0]*dt;
P[0][1]+=Pdot[1]*dt;P[1][0]+=Pdot[2]*dt;
P[1][1]+=Pdot[3]*dt
(8)计算角度偏量、卡尔曼增益。
angle_err=incAngle-angle
E=R_angle+P[0][0]
K_0=P[0][0]/E;K_1=P[1][0]/E;
Y_0=P[0][0];Y_1=P[0][1]
(9)更新协方差矩阵并给出最优估计值。
P[0][0]-=K_0*Y_0;P[0][1]-=K_0*Y_1;P[1][0]-=K_1*Y_0;P[1][1]-=K_1 *Y_1;
angle +=K_0*angle_err
(10)更新最优估计值偏差。
q_bias+=K_1*angle_err
通过上述步骤可以实现卡尔曼融合算法,将输入的陀螺仪和加速度计的数据进行融合,得到角度信息并返回。
文中使用C语言对卡尔曼滤波器进行建模得到上述程序。其中,dt代表了离散系统中对传感器陀螺仪和加速度计的采样时间。Q_angle和Q_gyro分别代表速度计和陀螺仪测量的协方差,协方差取值的物理意义是对传感器信号品质的一种评估。例如,如果认为加速度计测量的数据更可靠,就可以将Q_angle的值设置的较小,从而在滤波过程中体现这种可靠性。R_angle矩阵代表测量误差的协方差。同理,R取值的大小就代表测量噪声的大小。Q和R矩阵的取值,通过大量实验获取比较合理的参数值。
3 实验平台验证
结合上述对卡尔曼滤波算法的分析,采用加速度计MMA7260和陀螺仪ENC03作为惯性传感元件,对静态和动态的机器人姿态进行平台验证,结果如图3所示。
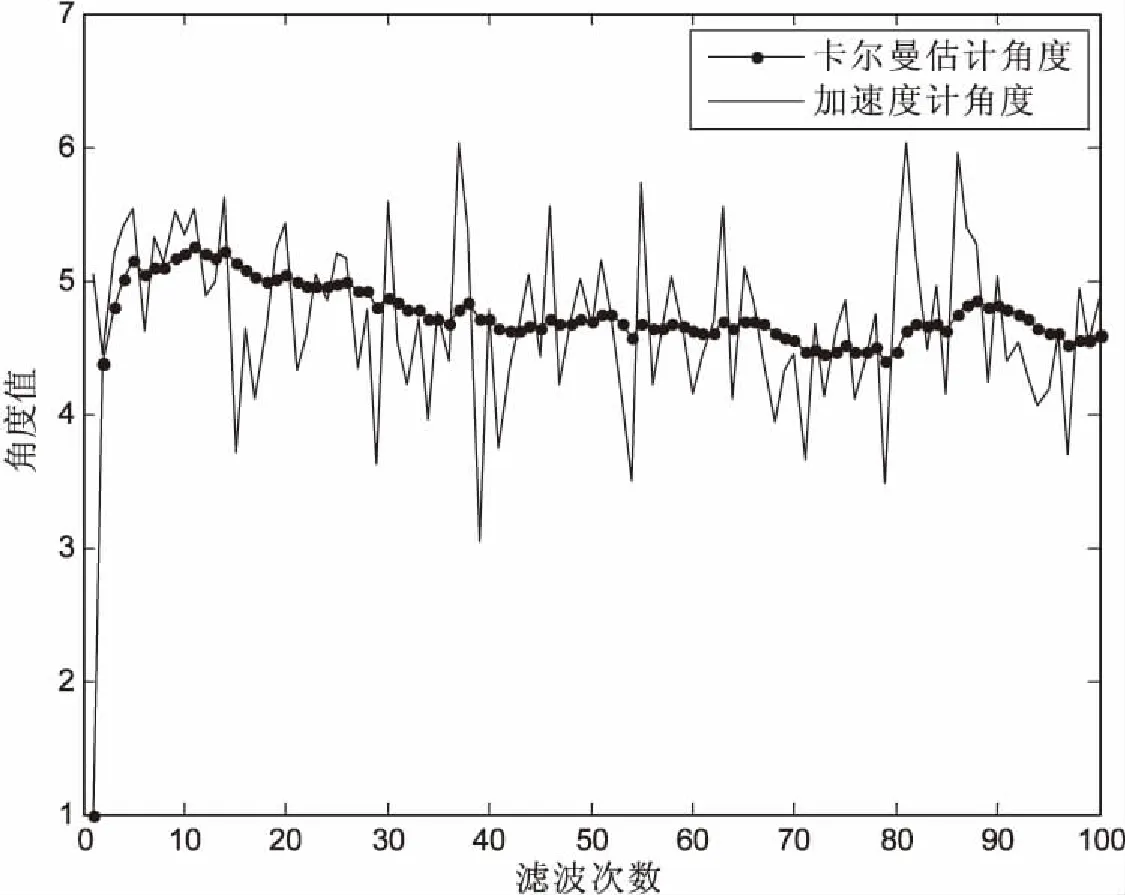
图3 卡尔曼数据融合后的效果
4 结束语
轮式自平衡机器人是一种通用的机器人。它适用于各种复杂环境中,通过陀螺仪和加速度计采集的数据可以控制其平衡性,但是效果不够好。为了进一步提高系统的性能,文中通过离散卡尔曼算法将ENC03陀螺仪和MMA7260加速度计采集的数据进行融合输出。分别研究了传统的卡尔曼算法,并详细推导了如何建立适合自平衡机器人的算法模型,最后介绍并实现该算法。通过实时监测(见图3)可以发现,在未进行角度融合之前,加速度计计算得出的角度在静态和动态都有着极大的噪声;经过卡尔曼滤波算法融合后的角度平滑稳定,达到了预期的效果。
[1] 王振宇.两轮移动机器人平衡控制系统的研发[D].成都:西南交通大学,2010.
[2] 王小冬.卡尔曼滤波在卫星导航中的应用研究[D].大连:大连海事大学,2008.
[3] 秦永元,张红钺,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,2012:33-42.
[4] 席 峰,刘 中.基于信息矩阵加权一致策略的分布式Kalman滤波器[J].信息与控制,2010,39(2):194-199.
[5] 杨元喜.动态Kalman滤波模型误差的影响[J].测绘科学,2006,31(1):17-18.
[6] 王学斌,徐建宏,张 章.卡尔曼滤波器参数分析与应用方法研究[J].计算机应用与软件,2012,29(6):212-215.
[7] 陆如华,徐传玉,张 玲,等.卡尔曼滤波的初值计算方法及其应用[J].应用气象学报,1997,8(1):34-43.
[8] 邱 恺,黄国荣,陈天如,等.卡尔曼滤波过程中的稳定性研究[J].系统工程与电子技术,2005,27(1):33-35.
[9] 潘 泉,于 昕,程咏梅,等.信息融合理论的基本方法与进展[J].自动化学报,2003,29(4):599-615.
[10] 崔平远,郑黎方,裴福俊,等.基于卡尔曼/粒子组合滤波器的组合导航方法研究[J].系统仿真学报,2009,21(1):220-223.
[11] Kalman R E.A new approach to linear filtering and prediction problems[J].Transaction of the ASME-Journal of Basic Engineering,1960,82:35-45.
[12] Saber R O,Shamma J S.Consensus filters for sensor networks and distributed sensor fusion[C]//Proc of IEEE conference on decision and control.Seville:IEEE Press,2005:6698-6703.
[13] Ren W,Beard R W,Kingston D B.Multi-agent Kalman consensus with relative uncertainty[C]//Proc of American control conference.Oregon:IEEE Press,2005:1865-1870.
[14] Marco C,Giorgio F,Riccardo G,et al.Real-time data fusion and MEMS sensors fault detection in an aircraft emergency attitude unit based on Kalman filtering[J].IEEE Sensors Journal,2012,12(10):2984-2992.
Research and Implementation of Data Fusion Algorithm for Self-balancing Robot
LV Chuan-long1,CAO Hua-jie2,LIU Hao-dong1
(1.School of Electrical Engineering,Southwest Jiaotong University,Chengdu 610031,China;2.School of Information Science and Technology,Southwest Jiaotong University,Chengdu 611756,China)
Self-balancing robot is general and uses the data collected by gyroscope and accelerometer to control its balance,which can be applied to various complex environments.In order to improve the response of the system because of its limited accuracy and punctuality,the discrete Kalman algorithm is utilized for fusion of the data acquired from the gyroscope (ENC-03) and accelerometer (MMA-7260).Research of the traditional Kalman algorithm is carried on,then establishment of its model for self balancing robot,finally introduction of its engineering implementation.According to the real-time monitoring,it can be seen that the angle calculated from the accelerometer without angle infusion has great noise both in its dynamic and static aspects.The angle acquired from Kalman filtering algorithm fusion is smooth and stable,achieving the desired effect.
self balancing robot;accelerometer;gyroscope;Kalman algorithm;data fusion
2015-10-15
2016-01-21
时间:2016-06-22
全国大学生创新基金资助重点项目(201310292023Z);江苏省“挑战杯-卓越杯”基金资助项目(201310292023Z)
吕传龙(1992-),男,硕士研究生,CCF会员,研究方向为机器人控制技术。
http://www.cnki.net/kcms/detail/61.1450.TP.20160622.0842.006.html
TP301.6
A
1673-629X(2016)08-0035-04
10.3969/j.issn.1673-629X.2016.08.007

