最大流问题的改进最短增广链算法
ZHAO Li-feng,JI Ya-bao
(College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)
最大流问题的改进最短增广链算法
在最大流问题中,由于Ford-Fulkerson算法中增广链选取的任意性,导致该算法不是有效的多项式算法。经典的最短增广链算法是通过在增广过程中寻找最短增广链,从而排除增广链选取的任意性。但计算过程中为寻找最短增广链,需要根据原网络循环地构建剩余网络和剩余分层网络,步骤非常繁杂。为改善以上不足,基于经典最短增广链算法,提出改进最短增广链算法。该算法的思想是:若在增广剩余分层网络中流值的过程中得到饱和弧,则删除该弧对应于原网络中的弧,使原网络得以简化,以此可降低构建剩余网络和剩余分层网络的复杂性,从而优化最短增广链算法。理论和仿真实验都表明,改进算法不仅正确,而且比原算法效率更高。
最大流;最短增广链;剩余网络;剩余分层网络
0 引 言
网络最大流问题是经典的组合优化问题,是网络流理论中的重要组成部分。最大流问题在现实生活中以及众多科学领域中都有着广泛的应用,例如常见的交通网络以及通信网络都可以转化成最大流问题来解决。因此网络流的研究具有重要的现实意义,它可以优化结构、提高效率、发挥最大的社会和经济效益。
对网络最大流理论的研究已经取得了大量成果,并且也形成了完善的理论体系。最大流问题的经典算法可以分为增载轨类算法和预留推进类算法[1]。在增载轨类算法中有1956年发现的Ford-Fulkerson算法[2]和Dinic等提出的改进Ford-Fulkerson算法(每次都沿着最短增广链增广)。Edmonds和Karp[3]提出利用剩余网络寻找最短增广链的最短增广链算法。Dinic[4]构建了阻塞流和分层网以设计最短增广链算法。预留推进类算法中包括由Goldberg和Tarjan提出的预流推进算法[5]。在这些研究之后又有一些针对特殊网络而提出的最大流问题的算法[6-12],包括对于稀疏网络、小容量网络、无向网络、点边有容量约束网络、节点环流型网络、单位容量网络等,文献[13-14]对经典的最大流算法进行了研究。
对于Dinic等基于最短增广链提出的最短增广链算法,需要循环构建剩余网络和分层网络,这个过程往往比较复杂。
文中在增广过程中删除某些已经不再增广的弧,从而简化了原网络,减少了构建剩余网络和分层网络的复杂性,优化了最短增广链算法。
1 相关知识
1.1 最大流问题线性规划模型
模型如下:
1.2 剩余网络
给定一个带发点vs和收点vt的容量网络N=(V,vs,vt,E,C)及N上的可行流f,定义
A(f)=A+(f)∪A-(f)
称cij(f)为弧(vi,vj)关于f的剩余容量。于是得到一个带发点vs和收点vt的容量网络N(f)=(V,vs,vt,A(f),cf),称之为N关于f的剩余网络。
1.3 剩余分层网络
对于N的关于f的剩余网络N(f)=(V,vs,vt,A(f),cf),定义N(f)的子网络EN(f)=(V'(f),A'(f),cf)如下:
V'(f)={vt}∪{vi∈V|h(vi) A'(f)={(vi,vj)∈A(f)|h(vj)=h(vi)+1 EN(f)称为N关于f的剩余分层网络。 2.1 最短增广链算法步骤 在网络N=(V,vs,vt,E,C)中,从任意一个可行流f(一般可取零流)开始,执行以下步骤: 步骤1:构造剩余网络N(f)并对其分层,构造剩余分层网络EN(f)。若EN(f)中y得不到标号,结束,f就是最大流,否则转步骤2。 步骤2:求EN(f)中vs→vt的一条路p,并沿路p增加流得到更大的流,并去掉EN(f)中所有饱和弧。 步骤3:求EN(f)中vs→vt的一条路p,若不存在则返回步骤1;否则返回步骤2。 2.2 改进算法思想 在最短增广链算法步骤3中,当EN(f)中不存在vs→vt路时,就返回步骤1,在步骤1中重新构造剩余分层网络。在这个过程中发现,对于步骤2中增广流后而得到的饱和弧在步骤1中的剩余分层网络并不存在,即最短增广链算法步骤2中增广流后而得到的饱和弧在以后的增广过程中这条弧的流值不可能增加或减少。 于是,在改进算法中,只需要删去原网络中的这些饱和弧,便可以简化步骤1中重新构造网络的过程。 2.3 改进算法正确性和时间复杂度 定理1:对于最短增广链上增广流值后而得到的饱和弧,在以后的算法进程中这条弧上的流值不可能再增加或减少。 证明:对这些饱和弧首先要构造剩余网络,再对其进行分层,最后构造出剩余分层网络。在剩余分层网络中寻找vs→vt路,对vs→vt路进行图中各个顶点的层次只可能增加或不变而不可能减少。已知在剩余分层网络中寻找的vs→vt路对应于原网络的增广链,现假设vs→vt路中的某条弧e对应于原网络增广链中的前向弧,则实际情况是对弧e增加流值,当增加流值未达到饱和时则在剩余分层网络中与弧e关联的节点的层次没有改变,若增加流值达到饱和时与在剩余分层网络中与弧e关联的节点层次就会增加。再假设vs→vt路中对应于原网络中的后向弧,则实际情况是对弧e减少流值,当减少流值未达到饱和时则在剩余分层网络中与弧e关联的节点的层次没有改变,若减少流值达到饱和时与在剩余分层网络中与弧e关联的节点层次就会增加。于是增流达到饱和的弧在重新构造剩余分层网络时不满足顶点层次要求,故不存在于重新构造的剩余分层网络中。即这条弧不可能存在于以后的增广过程中。 定理2:改进算法时间复杂度为O(n2m)。 证明:设容量网络D的顶点数为n,弧数为m。步骤1中最多执行n-1次,又由广探法知,每次构造剩余分层网络的复杂性为O(m)。步骤2和步骤3中最多增广m次,而每次增广的计算量为O(n),所以改进的最短增广链算法的算法复杂度为O(nm)+O(n2m)=O(n2m)。 2.4 改进算法步骤 步骤1:构造剩余网络N(f)并对其分层,构造剩余分层网络EN(f)。若EN(f)中y得不到标号,结束,f就是最大流,否则转步骤2。 步骤2:求EN(f)中vs→vt的一条路p,并沿路p增加流得到更大的流,并去掉EN(f)中所有饱和弧。 步骤3:求EN(f)中vs→vt的一条路p,若不存在,则将在步骤2中达到饱和的弧在原网络中删除,再返回步骤1;否则返回步骤2。 例:求图1中网络最大流。 图1 原网络图 图中,弧上的数字表示弧容量,初始流为零流。首先通过剩余分层网络,最短增广链为3条弧。通过步骤1~3得到增广流值如图2所示。流值为7,在增广流值的过程中弧(v2,v3)和弧(v1,v4)达到饱和,增广流值后EN(f)中不存在x→y的一条路p,即原网络中不存在只有3条弧的增广链。 图2 增广流值后的网络图 于是返回步骤1,在原网络中删除弧(v2,v3)和(v1,v2),再构建剩余分层网络,见图3。接着进行步骤2和步骤3,此时最短增广链v1→v2→v4→v5→v6含有4条弧。 图3 删除饱和弧(v2,v3)、(v1,v2) 增广流值后流值为8。在增广过程中弧(v4,v5)达到饱和,增广流值后EN(f)中不存在x→y的一条路p,即原网络中不存在只有4条弧的增广链。再返回步骤1在原网络中删除弧(v2,v3)、(v1,v4)和(v4,v5),再构建剩余分层网络,见图4,此时剩余分层网络中v6得不到标号。于是图4即为最大流,流值为8。 图4 删除饱和弧(v1,v4)后的剩余分层网络图 文中MATLAB仿真实验是在网络规模为500,1 500,2 500和3 500个节点的随机网络上对经典算法和改进算法的运行时间进行比较(见表1),针对每个规模的网络均进行十次实验求平均值。随机网络是由经典BA无标度网络的方法随机生成。 表1 两种算法所得到的最大流值 通过表1可以看出,两种算法同样都能求解出最大流,并且都能求出网络中每条弧中的具体流值(由于网络比较大,具体流值情况没有写入)。 图5的实验结果表明,改进算法相对于原算法节省了运行时间,这与之前的分析吻合,并且节点数越多,改进算法效率越高。 图5 算法运行时间对比 在网络最大流问题中最短链增广链算法是经典算法。该算法是对2F算法的改进,是一种强多项式算法,算法效率高。该算法对2F算法进行的改进是为了避免增广链选取的任意性,每次增广都通过构建剩余网络和分层网络来寻找最短增广链,从而使得算法的复杂性不再取决于网络容量,而仅仅取决于网络节点数和边数。但是构建剩余网络和分层网络均比较复杂。文中在算法循环进行的过程中不断简化需要构建的剩余网络和层次网络,从而减少了构建剩余网络和分层网络的复杂性。 [1] 张宪超,陈国良,万颖瑜.网络最大流问题研究进展[J].计算机研究与发展,2003,40(9):1281-1292. [2]FordLR,FulkersonDR.Maximumflowthroughanetwork[J].CanadianJournalofMath,1956,8(5):399-404. [3]EdmondsJ,KarpRM.Theoreticalimprovementsinalgorithmicefficiencyfornetworkflowproblems[J].JournaloftheAssociationforComputingMachinery,1972,19(2):248-264. [4]DinicEA.Algorithmsforsolutionofaproblemofmaximumflowinnetworkswithpowerestimation[J].SovietMathematicsDoklady,1970,11(8):1277-1280. [5] 谢 政.网络算法与复杂性理论[M].长沙:国防科技大学出版社,2003. [6] 赵礼峰,严子恒.基于增广链修复的最大流求解算法[J].计算机应用,2015,35(5):1246-1249. [7] 张宪超,陈国良.小容量网络上的最大流算法[J].计算机研究与发展,2001,38(2):194-198. [8] 邱伟星,王以凡,沈金龙.一个求无向网络最大流的算法[J].南京邮电学院学报,1997,14(4):170-172. [9] 郭 强.无向网络最大流问题研究[J].计算机工程与应用,2005,41(9):76-78. [10] 张宪超,江 贺,陈国良.节点和边都有容量的有向平面网络中的最小截和最大流[J].计算机学报,2006,29(4):544-551. [11] 徐光联,孙文新.节点环流网络中的最大流算法[J].应用科技,2014,41(1):48-53. [12] 张宪超,江 贺,刘馨月,等.无向平面单位容量网络中的最大流[J].计算机研究与发展,2008,45(S1):40-42. [13] 孙泽宇,丁国强,程志谦.网络最大流求解算法的研究[J].微计算机信息,2010,26(1-3):143-145. [14] 孙泽宇.基于标号法求解网络最大流算法的研究[J].甘肃联合大学学报:自然科学版,2009,23(4):64-66. 赵礼峰,纪亚宝 (南京邮电大学 理学院,江苏 南京 210023) Improved Shortest Augmenting Chain Algorithm of Maximum Flow In maximum flow problem,since the Ford-Fulkerson algorithm chooses arbitrarily augmented chain,as a result the algorithm is not a valid polynomial one.Classical shortest augmenting chain algorithm is to find the shortest augmenting chain in the augmented chain process,thus eliminating the arbitrary of augmented chain selection.But in calculation process for finding the shortest augmenting chain,needing to build the remaining network and the remaining surplus hierarchical network based on the original network cycle,its step is very complicated.In order to improve the above problems,based on the classical shortest augmenting chain algorithm,an improved one for the shortest augmenting chain is put forward.The idea is that if the saturated arc is obtained in flow value processing augmented remaining hierarchical network,then the original arc corresponding to the network is deleted,making the original network simplified in order to reduce the complexity of constructing remaining network and the remaining layered network and optimize the shortest augmenting chain algorithm.The theory and simulation show that the improved algorithm is not only correct,but also higher in efficiency than the original algorithm. maximum flow;shortest augmenting chain;remaining network;remaining layered network 2015-12-02 2016-03-09 时间:2016-08-01 国家自然科学基金青年基金项目(61304169) 赵礼峰(1959-),男,教授,硕士研究生导师,研究方向为图论及其在通信中的应用;纪亚宝(1990-),男,硕士研究生,研究方向为图论及其在通信中的应用。 http://www.cnki.net/kcms/detail/61.1450.TP.20160801.0907.044.html TP301.6 A 1673-629X(2016)08-0052-03 10.3969/j.issn.1673-629X.2016.08.011 ZHAO Li-feng,JI Ya-bao (College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)2 改进的最短增广链算法
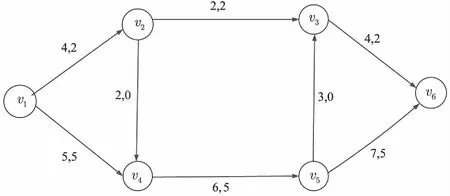
3 数值实例



4 算法的仿真与比较

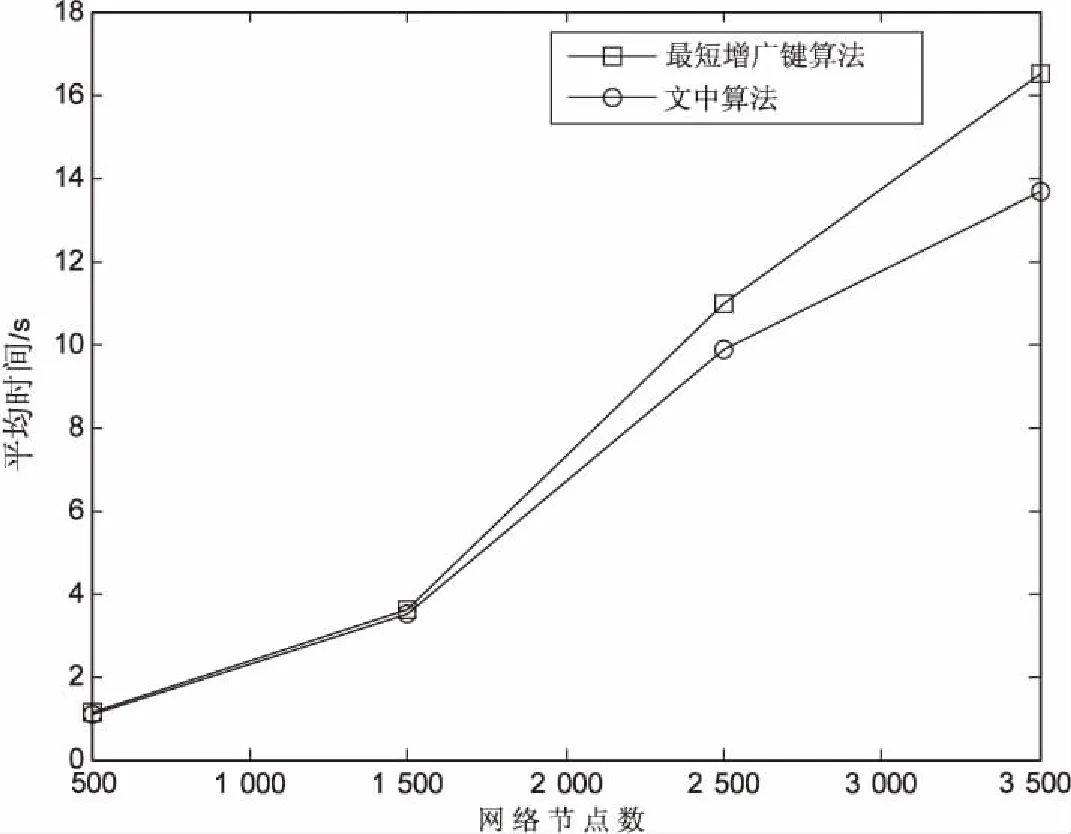
5 结束语

