基于模糊C均值聚类有效性的协同过滤算法
葛林涛,徐桂琼
(上海大学 管理学院,上海 200444)
基于模糊C均值聚类有效性的协同过滤算法
葛林涛,徐桂琼
(上海大学 管理学院,上海 200444)
针对电子商务系统中传统协同过滤算法普遍存在的稀疏性和扩展性问题,文中提出了基于模糊C均值聚类有效性的协同过滤算法。首先依据四种不同的聚类有效性函数确定合理的聚类数区间,并在合理聚类数区间中根据Xie-Beni方法搜寻得到最佳的聚类数,然后使用最佳聚类数对项目进行模糊C均值聚类,将用户对单个项目的偏好转化为对相似群组的偏好,将稀疏的用户-项目偏好信息构造成密集的用户-模糊类的偏好信息,最后在项目所属类别中寻找目标用户的最近邻并产生推荐。在数据集MovieLens上与传统推荐算法相比的实验结果表明,新算法在平均绝对偏差、召回率、准确覆盖率等方面都有了较大改善,提高了推荐质量。
协同过滤;模糊C均值聚类算法;聚类有效性函数;最佳聚类簇数
1 概 述
互联网已成为当下人们获取信息的一个重要途径。然而,随着互联网信息的不断增加,用户很难从中挑选出自己真正需要的信息。针对互联网中的“信息过载”问题,推荐系统作为一种有效的解决手段被广泛应用在电子商务领域,它能主动为用户推荐需要但无法轻易获取的信息,在提供更具针对性的个性化服务的同时也提高了电子商务网站的销售量。因此,推荐系统已成为当下电子商务应用领域中的研究热点。其中,协同过滤推荐算法是目前最流行和最成熟的推荐技术[1]。
然而在实际应用中,推荐系统存在两个问题:一是稀疏性,由于用户评价过的物品只占所有物品的一小部分,因此,用户-项目评分矩阵非常稀疏,从而影响推荐质量;二是可扩展性,随着系统中用户和资源的增多,性能越来越低。
针对以上问题,许多学者进行了深入研究并取得了一系列的研究成果[2-14]。其中,将聚类算法应用到推荐系统中有助于缓解数据的稀疏性问题。如文献[5-7]使用硬聚类算法K-means方法对用户进行聚类,减少了寻找最近邻的计算量,然而硬聚类算法很难符合一个项目可能同时属于几个类的实际情况,同时,为了确定最佳的聚类数目,要计算不同聚类数目下的MAE值,增加了计算复杂度。文献[8]综合考虑用户对项目的关注和用户评价的影响,提出了改进的用户聚类的协同过滤推荐方法,使用了用户对项目关注相似度来替代传统的相似度。文献[9]提出了基于用户谱聚类的协同过滤推荐算法,并使用组合相似度[10]在用户所属类中寻找最近邻并产生推荐,提高了推荐质量。文献[11-12]提出了基于模糊聚类的协同过滤算法,通过传递闭包法计算模糊相似关系,然后对项目进行聚类,缓解了由于用户项目评价数据稀疏而导致传统协同过滤中寻找最近邻居用户不准确的问题,然而在求解项目相似矩阵的过程中需要进行矩阵幂运算,当矩阵的阶数n较大时,工作量较大。文献[13-14]中将模糊C均值聚类应用到协同过滤算法中,有效缓解了数据稀疏性问题。文献[13]通过比较不同聚类数下的RMSE值,确定最佳聚类数,计算复杂度有待提高。文献[14]将用户数量的一半作为最佳聚类数,降低计算量,准确度有待提高。文献[15]对Xie-Beni方法[16]进行了证明与改进,提出了一种优化的最佳聚类数选择策略,在提高了算法的准确性的同时也减少了计算量。
基于以上研究工作,文中提出了一种基于模糊C均值聚类有效性的协同过滤算法(FCMCCF)。在使用模糊C均值聚类算法解决数据稀疏性问题的同时,引入聚类有效性判别函数,降低了寻找最佳聚类数的计算复杂度。在MovieLens公开数据集上的实验结果表明,提出的改进算法与传统协同过滤算法相比,较好地改善了平均绝对偏差、覆盖率、召回率指标,提高了推荐质量。
2 概念定义
2.1 协同过滤算法概述
协同过滤算法是推荐系统中应用最广、效果最好的算法之一。典型的协同过滤算法是基于用户的,其基本思想是通过用户-项目评分矩阵计算出用户之间的相似度,从中选出与用户最相似的前k个用户,根据这k个用户对当前用户的未评分项目的评分,预测当前用户对其未评分项目的评分,选出前n个推荐。协同过滤推荐算法的实现过程主要分为三步:
(1)建立推荐模型。
协同过滤算法的输入是一个m×n的用户评价矩阵R的数据,Rui表示第u个用户对第i项的评价值。一般把评分分成5个等级,评分越高说明这个用户对物品的评价越高。
(2)查找最近邻居。
通过计算目标用户与其他用户之间的相似度,找出与目标用户最相似的“最近邻居”集,即对目标用户u,Nu={N1,N2,…,Ni}。首先计算用户之间的相似度,可采用Pearson相关系数、Cosine相似性等度量方法。然后,对目标用户u产生一个以相似度sim(u,v)递减排列的“邻居集合”。由于修正余弦相似度的准确性较高,因此文中采用的是修正的余弦相似性,见式(1)。
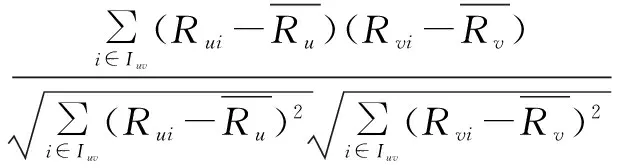
(1)
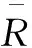
(3)进行推荐。
最后,根据目标用户的m个最近邻居对项目的评分,可以进行该用户对其未评分项目的评分预测。计算方法如下:
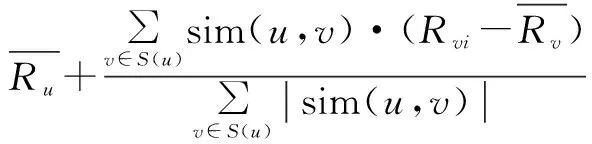
(2)
其中,Pui代表目标用户u对任意项目i的预测评分;S(u)表示邻居用户集合。
在预测出目标用户对未评价项目的评分后,使用TOP-N方法挑选出预测评分最高的N项,并对用户进行推荐。
2.2 模糊C均值聚类算法简介
聚类算法往往分为硬聚类算法和软聚类算法。将每个数据对象归到一个类被称为硬聚类算法,然而数据对象经常可以被归到几个类中,属于每个类的程度也不相同。因此,Ruspini和Bezdek于1981年提出了C均值的改进算法—模糊C均值聚类算法(FCMC)[17]。模糊C均值聚类算法相比于其他算法,具有简单、高效等特点,因此应用在很多领域。模糊C均值聚类算法属于一种有效的软聚类算法,根据每个样本隶属于某个类的程度(即隶属度)来对样本进行聚类,所以模糊C均值聚类算法在复杂的样本上也可以得到比较好的聚类效果[18-19]。
对于论域中的有限个对象集合{X1,X2,…,Xn},对于每个数据样本属于某个类别的程度,在模糊C聚类算法中,使用隶属度来定义。例如对于n个向量Xi(i=1,2,…,n)来说,FCMC首先将它们分成c个模糊组,然后求出每个类别的聚类中心,同时,要最优化价值函数(见式(3)),也就是将非相似性指标值达到最小。
(3)
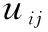
使式(3)达到最小的必要条件为:
(4)
(5)
FCMC算法包括以下四个步骤:
步骤1:随机生成0到1之间的数,并用来随机化隶属度矩阵U。
步骤2:用表示价值函数最优化条件(见式(4))计算出c个聚类中心ci,i=1,2,…,c。
步骤3:用式(3)计算价值函数。如果它相对上次价值函数值的改变量小于某个阈值,或者大于某个阈值,那么算法停止。
步骤4:用隶属度(见式(5))重新计算隶属度矩阵U,然后重复步骤2。
尽管FCMC算法能快捷地判定数据集中样本的类别,但是该算法属于无监督学习,必须先确定一个聚类簇数。如何确定最佳的聚类簇数以达到最好的聚类效果便是聚类有效性问题。
3 基于模糊C均值聚类有效性的协同过滤算法
在协同过滤推荐算法中,影响推荐精度的关键问题在于用户评分数据的极度稀疏性。事实上,由于协同过滤是在有相似爱好的用户间进行的,用户更可能选择有相似特征的项目。因此,可以用FCMC算法将属性特征上相似的项目聚成一类,然后在一类项目中寻找用户的最近邻居,以提高协同过滤算法的精度。
基于FCMC的协同过滤算法的关键在于确定最佳聚类数cmax。因此,文中首先计算不同聚类的有效性函数值,然后采用改进的Xie-Beni方法[15]选择cmax。
3.1 四类有效性函数
模糊C均值聚类算法属于无监督学习,为了确定FCMC算法的最佳聚类数,国内外学者提出了一些有效性判别函数,主要分为两类:
一类是基于模糊划分的方法,认为好的聚类对应于数据集是较分明较清晰的,代表函数如Bezdek提出的分割系数VPC和分割熵VPE[20];
另一类是基于几何结构的方法,认为每个子类应当是紧致的子类与子类相互间尽可能分离,代表函数有Xie和Beni的VXB[16]、Fukuyama和Sugeno的VFC[21]、Kwon的VK[22]等。
(6)
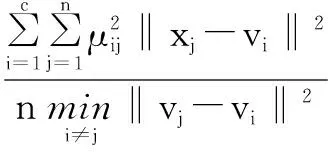
(7)
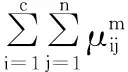
(8)
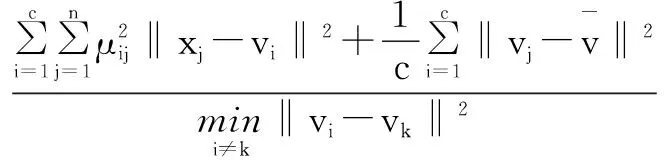
(9)
事实上在评价聚类结果时这四个有效性函数不一定同时达到最优,FCMC算法中最优的聚类数的确定至今没有一个最优准则,只能结合多个有效性判别函数对最优聚类数进行判断。然而,通常这样认为:在多个有效性函数取得较优值对应的聚类数为最佳聚类数。
3.2 算法描述
基于模糊C均值聚类有效性的协同过滤算法(FCMC CF)的具体步骤如下:
步骤1:最佳聚类数的确定。
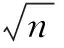
步骤2:构造用户-模糊簇评价偏好矩阵。
用cmax对项目进行FCMC聚类,产生相应的模糊簇,并用式(10)计算每个项目对应某个模糊簇中的隶属度。
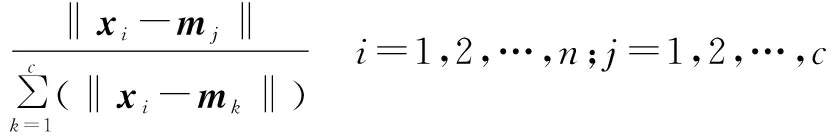
(10)
其中,xi为每个项目的属性特征向量;mj代表每个模糊簇中心的属性特征向量;‖xi-mj‖为项目i与模糊簇j的相近程度(即欧几里德距离);c代表模糊簇的数目。
通过原始稀疏用户-项目评价矩阵中的评分值和隶属度矩阵中项目属于某个模糊簇的隶属度,可以通过式(11)来计算得到用户对某个模糊簇的偏好值,并构造出如表1所示的用户-模糊簇的偏好矩阵UC,相对来说该矩阵比原始矩阵的稀疏性较低。
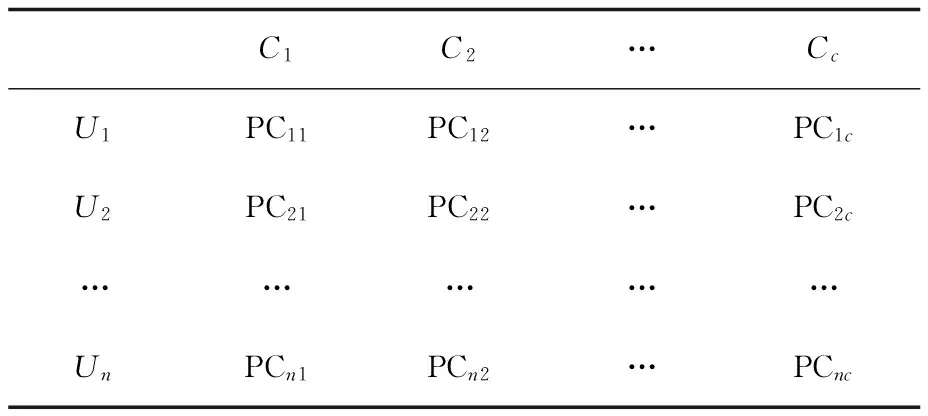
表1 用户-模糊簇评价矩阵
其中,偏好值的计算如式(11)所示:
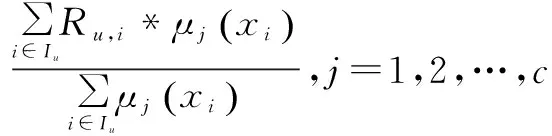
(11)
其中,PCu,j为用户u对模糊簇j的评价值;Ru,i为用户u对模糊簇j中的项目i的评价值;Iu为所有用户u已经评价的项目集合。
步骤3:计算用户的最近邻居集合。
使用上一步计算出来的稀疏性较低的用户-模糊簇偏好矩阵来计算并形成目标用户的最近邻集合。用户u和v之间的相似度按式(1)计算。
步骤4:为目标用户形成推荐。
从用户最近邻集合中选出目标用户的K个近邻,并根据式(2)来预测目标用户对没有评分过的项目的评分。然后,对预测评分进行排序,使用TOP-N策略进行推荐,即筛选出最高的N项推荐给目标用户。
4 实验与结果分析
4.1 数据集和度量标准
文中在实验中使用的数据是美国Minnesota大学GroupLens项目组提供的Movielens数据集ml-100k中的u2数据。该数据集包含了943名用户对1 682部电影的评价(评分值为数字1到5,如果数值越高则用户喜爱该电影的程度越高),并含有电影项目的分类特征。该数据集仅包含评价过20部以上电影的用户评价数据,没有评分的电影数据占所有数据的比重(稀疏度)为93.7%。
文中使用平均绝对偏差(MAE)、召回率(Recall)和覆盖率(Coverage)来度量算法的推荐质量。其中,MAE表示推荐算法对目标用户的预测评分与目标用户的实际评分的偏差值,这个指标可以用来评价推荐算法做出预测的误差,如果推荐质量越高,那么MAE的值越小。MAE定义为:
(12)
一般来说,Recall和Coverage可以较好地评价某个网站对目标用户做出推荐的预测准确率。
推荐结果的召回率定义为:
(13)
推荐结果的覆盖率定义为:
(14)
4.2 实验结果
通过选取电影所属的类型作为项目的属性特征,文中做了以下几个实验来验证提出推荐算法的有效性。
(1)确定最佳聚类数。
首先,通过比较不同聚类数相应的聚类有效性函数值来选出最佳聚类数cmax。实验结果如图1所示,具体的函数值如表2所示。
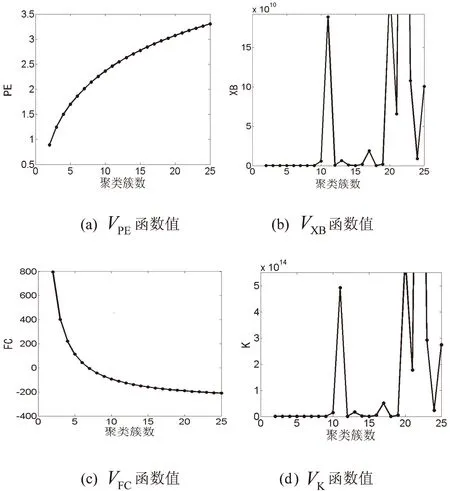
图1 不同聚类数对应的聚类有效性函数值 表2 不同聚类数对应的有效性函数值
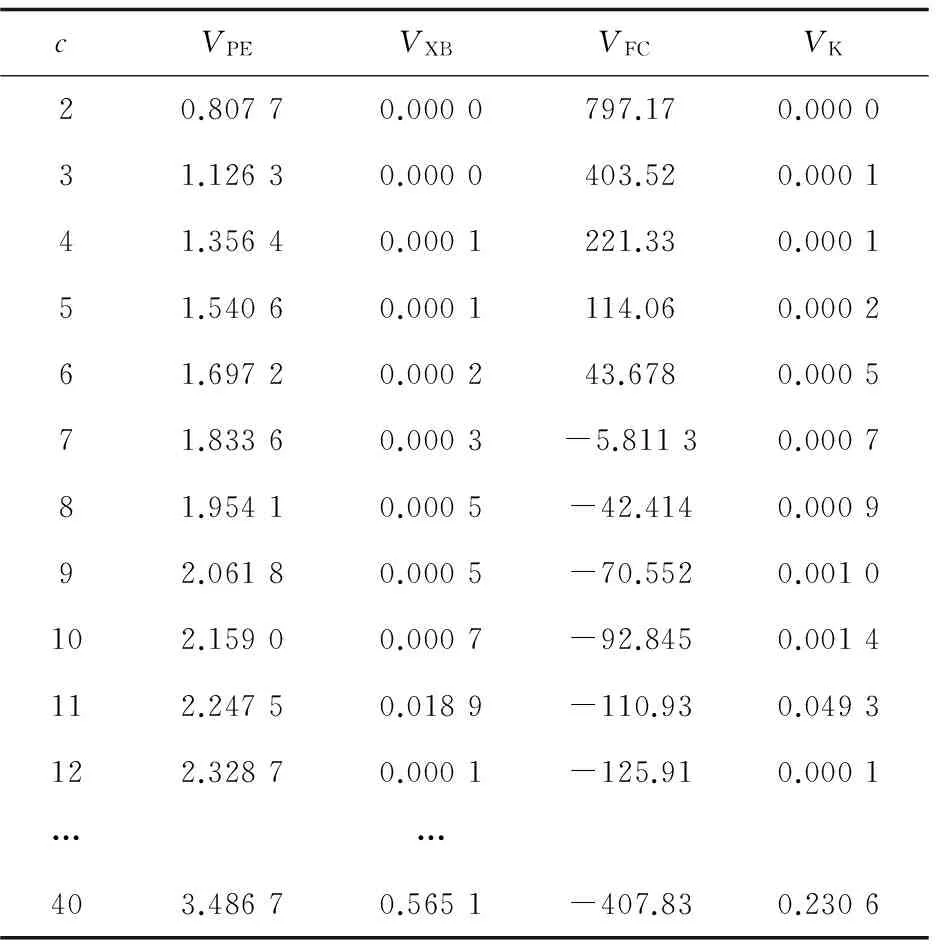
cVPEVXBVFCVK20.80770.0000797.170.000031.12630.0000403.520.000141.35640.0001221.330.000151.54060.0001114.060.000261.69720.000243.6780.000571.83360.0003-5.81130.000781.95410.0005-42.4140.000992.06180.0005-70.5520.0010102.15900.0007-92.8450.0014112.24750.0189-110.930.0493122.32870.0001-125.910.0001……403.48670.5651-407.830.2306
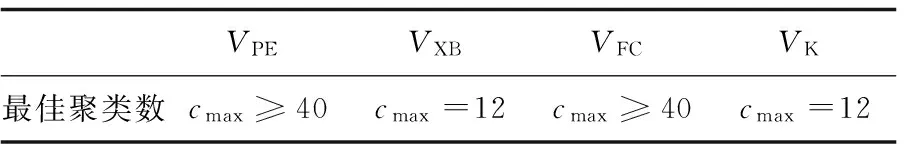
表3 Xie-Beni方法确定的cmax
(2)MAE比较。
使用上面得到的最优聚类数cmax对训练数据集合进行模糊C均值聚类,并比较了传统的协同过滤推荐方法(CF)和K-means聚类协同过滤推荐方法(KmeansCF)的结果,如图2所示,取最优聚类数cmax为12的实验结果。
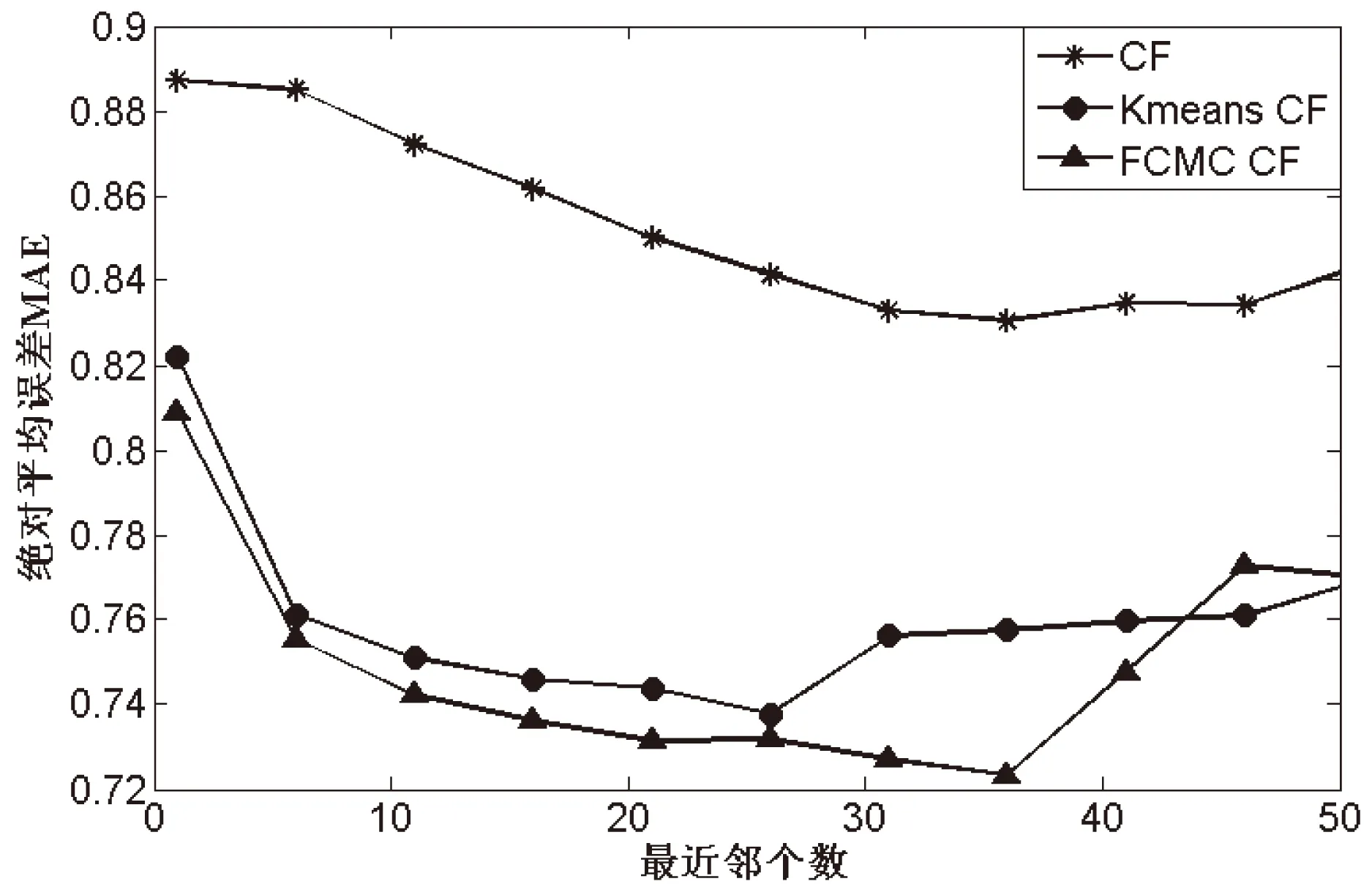
图2 不同算法MAE的比较
实验结果表明,FCMC得到的MAE值要优于CF算法和KmeansCF。
(3)召回率和覆盖率的比较。
在接下来的TOP-N实验中,选择FCMCCF算法与CF和KmeansCF在召回率、覆盖率指标上进行比较。结果如图3和图4所示。
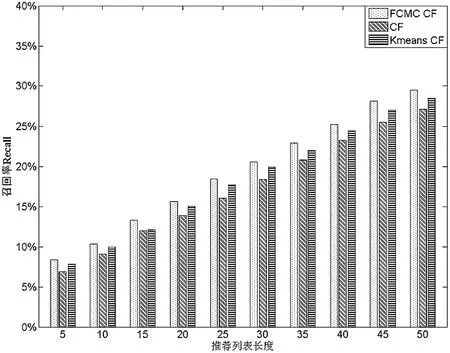
图3 不同算法召回率的比较
4.3 实验结果分析
如图2~4所示,FCMC CF算法在不同的最近邻水平下比CF算法以及Kmeans CF算法具有较小的MAE值,即新算法在推荐精度上有所改善;同时,FCMC CF算法在不同的最近邻水平下比CF算法以及Kmeans CF算法具有更高的召回率和覆盖率,有效地改进了推荐精度。
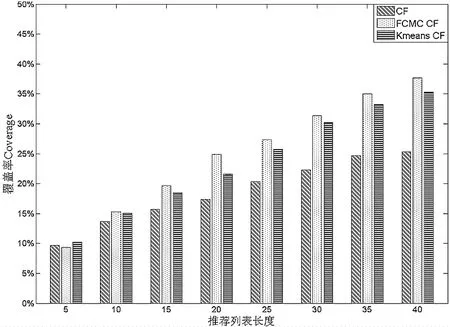
图4 不同算法覆盖率的比较
5 结束语
当下,电子商务的流行导致了电商网站的规模越来越大,与此同时,网站上的用户和物品数据也随之增长,推荐系统面临着数据稀疏与可扩展性问题。
针对以上问题,文中提出基于模糊C均值聚类有效性的协同过滤算法。首先通过聚类有效性函数和改进的Xie-Beni方法[15]确定了FCMC算法的最佳聚类数。其次根据属性特征对项目进行FCMC聚类,缓解了数据的稀疏问题,通过与Kmeans CF实验进行比较,更符合一个项目可能同属于几个类的实际情况。最后,对密集的用户-模糊簇的评价偏好矩阵进行协同过滤,由于簇的数目远远小于项目的数目,降低了推荐算法在时间上的计算复杂度。
该算法在MovieLens数据集上的实验结果表明,它可以较好地提高推荐系统的MAE、召回率和覆盖率。然而,该算法在不同数据集上评价标准下的表现还需要进一步的研究才能证实。此外,社交媒体的流行为推荐系统提供了更多的用户社会信息,因此,如何将其应用到推荐系统中也值得进一步研究。
[1] Resnick P,Varian H R.Recommender systems[J].Communications of the ACM,1997,40(3):56-58.
[2] Sarwar B,Karypis G,Konstan J,et al.Analysis of recommendation algorithms for e-commerce[C]//Proceedings of the 2nd ACM conference on electronic commerce.[s.l.]:ACM,2000:158-167.
[3] Konstan J A,Miller B N,Maltz D,et al.GroupLens:applying collaborative filtering to Usenet news[J].Communications of the ACM,1997,40(3):77-87.
[4] 邓爱林,朱扬勇,施伯乐.基于项目评分预测的协同过滤推荐算法[J].软件学报,2003,14(9):1621-1628.
[5] 邓爱林,左子叶,朱扬勇.基于项目聚类的协同过滤推荐算法[J].小型微型计算机系统,2004,25(9):1665-1770.
[6] Acilar A M,Arslan A.A collaborative filtering method based on artificial immune network[J].Expert Systems with Applications,2009,36(4):8324-8332.
[7] Tsi C F,Hung C.Cluster ensembles in collaborative filtering recommendation[J].Applied Soft Computing,2012,12(4):1417-1425.
[8] 查文琴,梁昌勇,曹 镭.基于用户聚类的协同过滤推荐方法[J].计算机技术与发展,2009,19(6):69-71.
[9] 李振博,徐桂琼,査 九.基于用户谱聚类的协同过滤推荐算法[J].计算机技术与发展,2014,24(9):59-62.
[10] 查 九,李振博,徐桂琼.基于组合相似度的优化协同过滤算法[J].计算机应用与软件,2014,31(12):323-328.
[11] 张海燕,顾 峰,姜丽红.基于模糊簇的个性化推荐方法[J].计算机工程,2006,32(12):65-67.
[12] 李 华,张 宇,孙俊华.基于用户模糊聚类的协同过滤推荐研究[J].计算机科学,2012,39(12):83-86.
[13] Birtolo C,Ronca D,Armenise R,et al.Personalized suggestions by means of collaborative filtering:a comparison of two different model-based techniques[C]//Proceedings of 2011 third world congress on nature and biologically inspired computing.[s.l.]:[s.n.],2011:444-450.
[14] 张付志,常俊风,周全强.基于模糊C均值聚类的环境感知推荐算法[J].计算机研究与发展,2013,50(10):2185-2194.
[15] 于 剑,程乾生.模糊聚类方法中的最佳聚类数的搜索范围[J].中国科学:E辑,2002,32(2):274-280.
[16] Xie X L,Beni G.A validity measure for fuzzy clustering[J].IEEE Trans on Pattern Analysis and Machine Intelligence,1991,13(8):841-847.
[17] Bezdek J C.Pattern recognition with fuzzy objective function algorithms[M].New York:Plenum Press,1981.
[18] Berget L,Mevik B H,Nis T.New modifications and applications of fuzzy C-means methodology[J].Computational Statistics & Data Analysis,2008,52(5):2403-2418.
[19] 马 军,邵 陆.模糊聚类计算的最佳算法[J].软件学报,2001,12(4):578-581.
[20] Bedzek J C.Cluster validity with fuzzy sets[J].Journal of Cybernetics,1973,3(3):58-72.
[21] Fukuyama Y,Sugeno M.A new method of choosing the number of clusters for the fuzzy c-means method[C]//Proceedings of the fifth fuzzy systems symposium.[s.l.]:[s.n.],1989:247-250.
[22] Kwon S H.Cluster validity index for fuzzy clustering[J].Electronics Letters,1998,34(22):2176-2177.
A Collaborative Filtering Algorithm Based on Fuzzy C-means Clustering Validity
GE Lin-tao,XU Gui-qiong
(School of Management,Shanghai University,Shanghai 200444,China)
Considering the sparsity and the scalability of traditional collaborative filtering recommendation algorithms in electronic commerce system,a new collaborative filtering algorithm is presented based on fuzzy C-means clustering validity.Firstly,a reasonable cluster number range is presetted,and then an optimal cluster number is determined based on some representative fuzzy clustering validity functions and Xie-Beni method.Secondly,using the optimal number of cluster,this algorithm transforms the users’ preferences of single item to similar groups with fuzzy C-means clustering,and sparse user-item preferences is established to dense user-fuzzy preferences.Finally,according to the item’s cluster it finds the nearest neighbors of the object user and generates recommendations.The experimental results in MovieLens show that the new algorithm improves recommendation quality in MAE,recall and coverage.
collaborative filtering;fuzzy C-means clustering;clustering validity;optimal number of clustering
2015-04-30
2015-08-06
时间:2016-01-04
国家自然科学基金资助项目(11201290,61104042)
葛林涛(1990-),男,硕士研究生,研究方向为数据挖掘、个性化推荐;徐桂琼,博士,教授,博士生导师,研究方向为数据挖掘与人工智能、复杂系统建模。
http://www.cnki.net/kcms/detail/61.1450.TP.20160104.1505.028.html
TP391
A
1673-629X(2016)01-0022-05
10.3969/j.issn.1673-629X.2016.01.005

