一种基于亚像素角点的SIFT立体匹配算法研究

洪 磊,嵇保健,洪 峰

(1.南京工程学院 汽车与轨道交通学院,江苏 南京 211167；2.南京工业大学 自动化与电气工程学院,江苏 南京 211800；3.南京航空航天大学 电子信息工程学院,江苏 南京 210016)

一种基于亚像素角点的SIFT立体匹配算法研究

洪 磊1,嵇保健2,洪 峰3

(1.南京工程学院 汽车与轨道交通学院,江苏 南京 211167；2.南京工业大学 自动化与电气工程学院,江苏 南京 211800；3.南京航空航天大学 电子信息工程学院,江苏 南京 210016)

针对尺度不变特征变换(SIFT)算法在立体匹配应用中实时性差、误匹配、特征点无鲜明几何意义等问题，提出了一种新的基于亚像素角点的SIFT立体匹配算法。该算法首先提取图像角点作为特征点，并通过拟合内插法精确定位其亚像素坐标。在角点邻域内利用图像的梯度信息构造基于梯度直方图统计信息的特征描述子，最后通过对特征描述子的对称性相似度测量以及随机采样一致性筛选获得最终的目标匹配点。实验结果表明，该方法在保持较强鲁棒性的基础上，较大幅度地提高了算法的实时性能和匹配精度。

立体匹配;亚像素角点;尺度不变特征变换;机器视觉

0 引 言

立体匹配是立体视觉技术中的重要组成部分，其本质是通过给定一幅图像中的一个点，寻找另一幅图像中的对应点，使得这两点为空间同一物体点的投影。由于立体视觉技术建立在对应点的视差之上，因而图像中对应点的匹配关系成为了机器视觉中一个极为重要的难点问题，在机器人视觉、航空测绘、医学诊断、虚拟现实技术等领域得到了广泛应用。传统上，有基于图像灰度的匹配、基于图像特征和基于解释的匹配或者多种方法相结合的立体匹配方法[1]。

由于传统直接利用局部灰度特征进行相关匹配的方法对噪声和灰度的非线性变换极为敏感，近年来很多学者对灰度变化梯度、领域灰度统计信息等间接利用图像灰度值特征的方法进行了广泛研究[2-4]。其中，Lowe D G提出的SIFT是目前最成功的局部特征提取算子[5]。SIFT以图像尺度空间极值点为特征点，通过对每个特征点进行精确定位、主方向选择及灰度梯度直方图统计生成特征点描述子。研究表明，SIFT特征点定位准确，具有很好的尺度、旋转、视角和光照不变性，优于其他局部特征提取算子。目前，SIFT已成功应用于目标识别、图像视频检索、全景拼接和视觉定位等领域。不过SIFT提取的特征也存在如下不足[6]：

(1)其特征点不是人们视觉意义上的角点，缺乏鲜明的几何意义；

(2)SIFT特征计算复杂度高且运算量大，其实时性较差，难以应用于对实时性要求较高的系统；

(3)SIFT特征点数量庞大，增加了特征匹配的时间负担，增大了误匹配率，降低了算法运行效率。

针对上述不足，文中提出了一种新的基于亚像素角点的SIFT立体匹配算法。该算法首先提取具有鲜明几何意义的角点作为特征点，通过拟合内插法精确地定位其亚像素坐标；然后在角点领域内，利用图像的梯度信息构造基于梯度直方图统计信息的特征描述子，最后对特征描述子进行对称性相似度测量，并采用随机采样一致性算法进行筛选，以确定最终匹配点。实验结果表明，该方法提高了匹配精度，降低了算法时间复杂度和误匹配率，在保持了SIFT算法较强鲁棒性的基础上，弥补了其实时性差、误匹配、特征点无鲜明几何意义的缺点，在机器视觉系统中具有一定的实用性。

1 算法原理

1.1 算法框架及流程

对于任何一种立体匹配方法，其有效性依赖于3个问题的解决，即选择正确的匹配特征、寻找特征间的本质属性及建立能正确匹配所选特征的稳定算法[7]。从上述三个方面出发，文中建立的算法基本框架如图1所示。

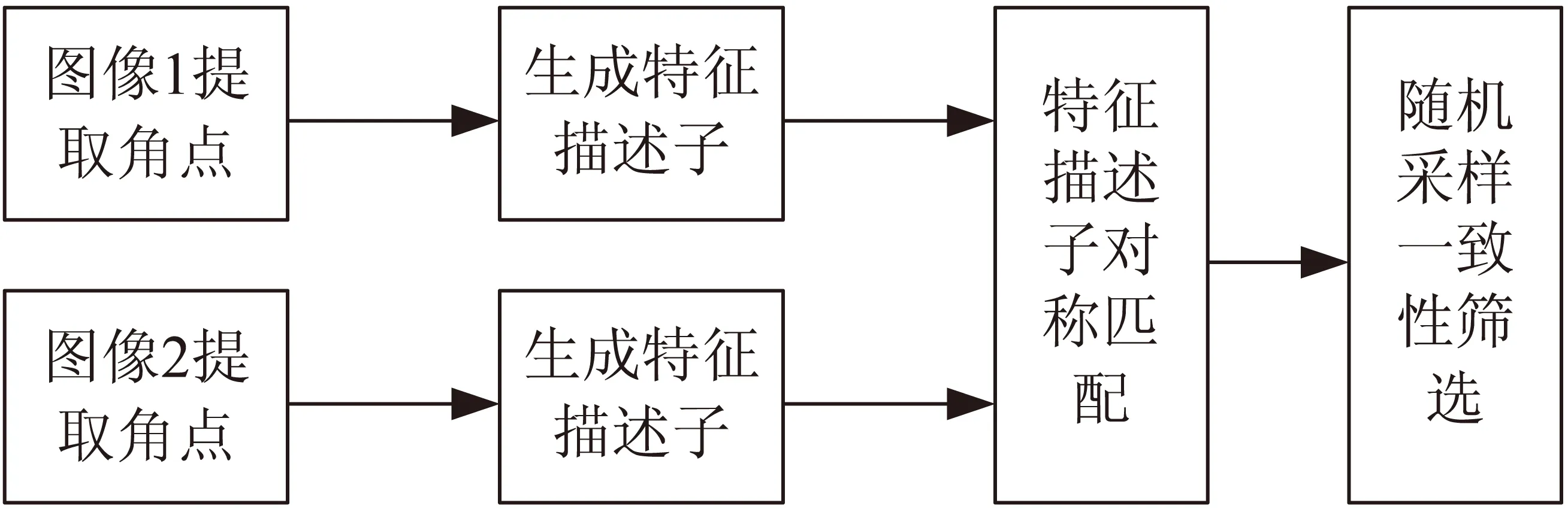
图1 算法框架图

假设工作环境中两幅图像拍摄的光照条件相当，若寻找两幅图像对应的匹配点，具体实现流程如下：

(1)载入两幅待匹配的图像数据；

(2)分别提取两幅图像的角点，确定每个角点的亚像素坐标；

(3)对于每个提取的角点，计算其邻域内的梯度方向直方图，生成SIFT特征描述子；

(4)通过计算两幅图像各角点特征描述子之间的欧氏距离，进行对称性相似度测量，利用近似最近邻算法确定初始匹配点对；

(5)以初始匹配点对为样本集，采用随机采样一致性算法进行匹配筛选，剔除误匹配及冗余匹配之后，确定最终匹配点对。

1.2 基于Harris算子的亚像素角点提取

图像中的角点具有鲜明的几何意义，保留了图像丰富的信息量，易于测量和表示，应用十分广泛。目前常见的角点检测算子主要有Moravec算子、Forstner算子、Harris算子和SUSAN算子[8-10]等。其中，Harris算子对摄像机姿态及光照的变化具有较好的稳定性，计算简单，角点提取可靠性高，非常适合相对复杂背景和光线不均匀性的特点，故文中采用Harris算子进行角点提取。

但是Harris算子的定位性较低，其探测精度是像素级的，而一般来说角点的位置并不恰好位于某像素的正中位置，所以Harris算子仅能得到角点位置的近似值，这对后续计算带来了误差。为此文中算法在Harris角点检测的基础上，通过对角点子域的像素灰度进行拟合内插，获取亚像素角点坐标。如图2所示，其中点C是角点的实际位置。

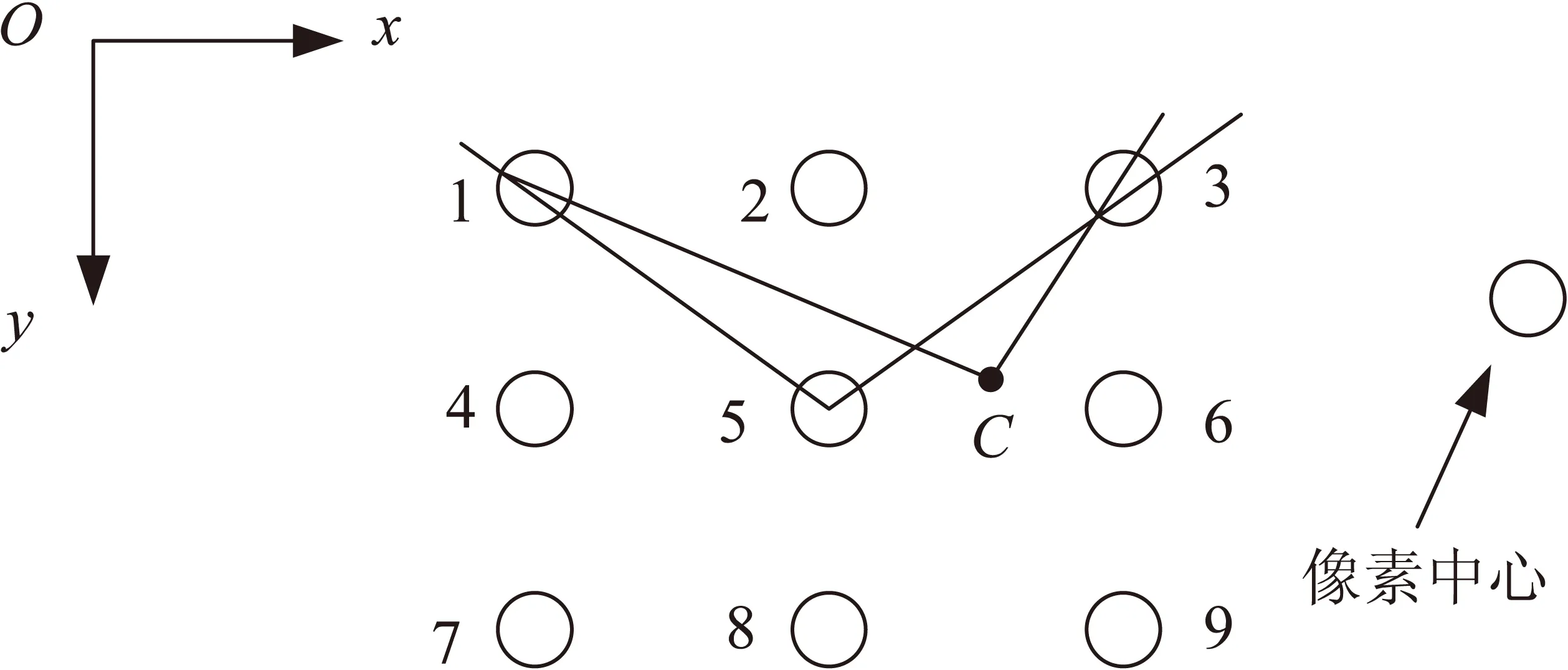
图2 角点子域的像素灰度内插

拟合曲面通常采用高斯曲面，其函数为：

(1)

其中，拟合出的(x0,y0)即为角点的内插位置。

由于高斯函数具有可分离的性质，因此有：

(2)

利用式(2)使二维高斯曲面拟合由两个一维高斯曲面拟合来完成，简化了拟合过程。通过高斯曲面拟合内插后的角点探测精度为亚像素级，在算法编程上，可利用OpenCV提供的cvGoodFeaturesToTrack和cvFindCornerSubPix函数来实现[11]。

1.3 特征描述子的生成

特征描述子的生成首先建立在特征提取的基础上。SIFT特征点在实际应用中由于缺乏直观几何意义,存在一定的局限性。为弥补这一不足，文中采用角点代替SIFT原有的特征点，以角点周围的图像梯度变化信息，构造基于三维梯度方向直方图的区域性特征描述子，见图3。

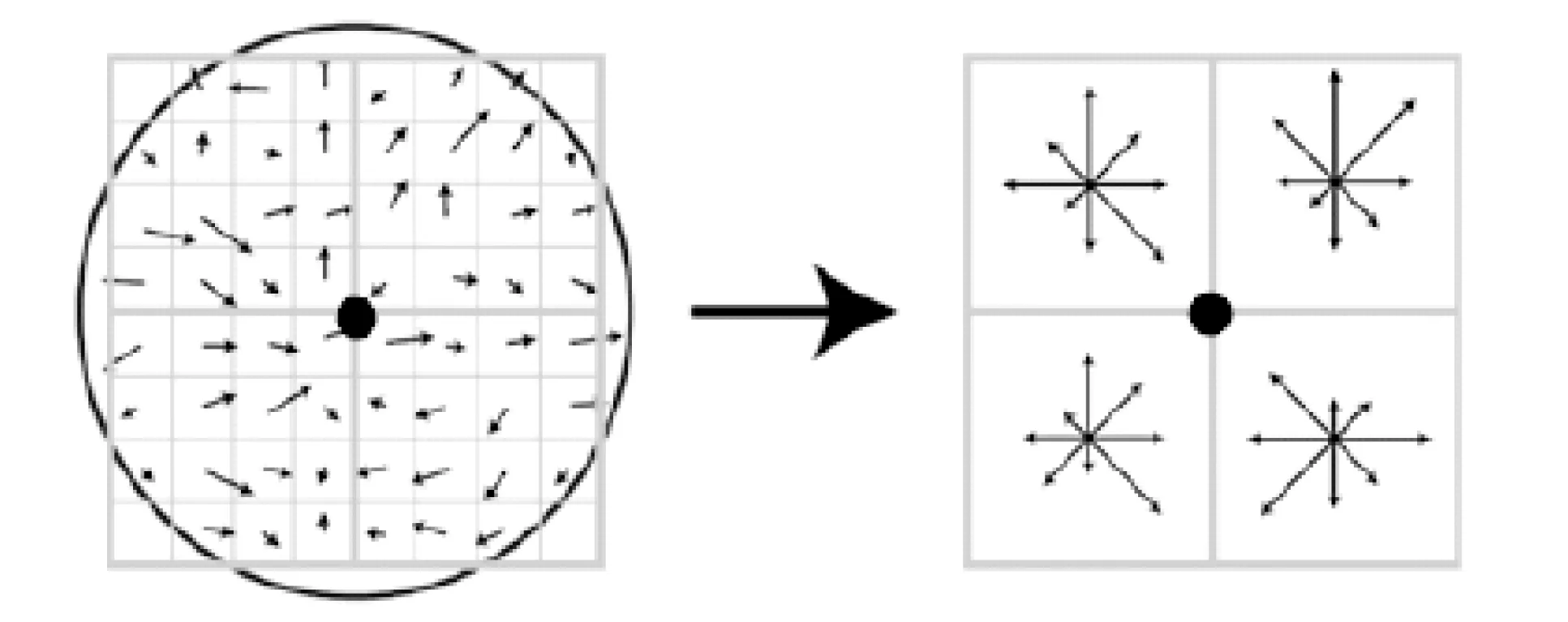
图3 由角点领域梯度信息生成特征描述子

具体生成方法如下：

(1)如图3所示，以角点为原点，沿图像x,y轴方向建立初始主坐标系，计算角点的梯度方向作为主方向。

(2)以角点为中心，选取大小为8×8的窗口，其中每个小窗口含3×3个像素。首先将初始主坐标系x轴旋转至与描述子主方向重合位置，得到实际主坐标系以获得旋转不变性，然后计算每个小窗口中心像素的梯度加权幅值与方向，公式如下：

m(x,y)=[(f(x+1,y)-f(x-1,y))2+ (f(x,y+1)-f(x,y-1))2]1/2

θ(x,y)=tan-1((f(x,y+1)-f(x,y-1))/ (f(x+1,y)-f(x-1,y)))

(3)

(3)以特征角点为中心，分别对左上、右上、左下、右下四个4×4窗口区域中的每个原子窗口中心像素计算其相对于主坐标系x轴的梯度方向，并通过近似判定将其分类到八个方向之一(如图3右所示)，最后依据其加权幅值的大小在每个方向上进行累加统计出其直方图。

(4)按左上、右上、左下、右下的顺序，以相对于每个4×4窗口中心点的八个方向的向量统计长度生成2×2×8即32维特征向量，将其进行归一化处理以消除光照不均匀的影响，最终得到特征描述子。Lowe指出，当以特征点为中心选取16×16窗口，也即形成4×4×8=128维特征向量时，该特征描述子拥有最佳匹配特性。文中为降低算法的时间复杂度，采用32维特征向量。

1.4 基于近似最近邻算法的特征匹配

当两幅图像特征点的特征描述子向量生成后，需进行特征点匹配，设图像1和2的第i个特征点描述子分别为:Ri=(ri1,ri2,…,ri32),Si=(si1,si2,…,si16)。

采用特征描述子向量之间的欧氏距离作为两幅图像中特征点的相似性判定度量，即：

(4)

要得到配对的特征点描述子(Ri,Si)，这里采用最近邻和次近邻特征点距离之比来减小误匹配的情况。即满足式(5)：

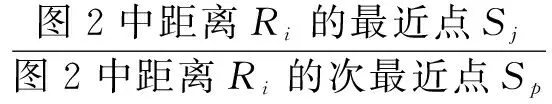
(5)

降低比例阈值Threshold，特征点的匹配点数目会减少，但稳定性更强。在文中实验，最近邻特征点距离与次近邻特征点距离之比取0.5。

对于最邻近及次邻近的特征点的搜索，最简单的方法是采用线性扫描，即穷举法，但由于特征点数量较大，故穷举法的时间复杂度很大，不适合实时应用。JonLouisBentley提出了Kd树搜索算法[12]，该方法将待查询特征点集构造为称作Kd树的数据结构，并提供了一种类似二叉树查询的高效搜索机制，从而大大降低了寻找最佳匹配的计算量。Kd树法在空间维数K较低时效率非常高，但对于K较大(K>10)时,其执行效率较低。此时Kd树法表现出较差的搜索效率，基本等同于穷举法，因此亦不实用。

针对Kd树算法的不足，文中采用近似最近邻算法即BBF(Best-Bin-First)算法[13]。该方法是对Kd树算法的改进，它采用一个优先级队列优化了Kd树对其节点的搜索顺序，并限定了搜索的最大次数，从而能快速地找到最近邻和次近邻点。由于文中采用的SIFT特征描述子具有32维，属于高维度空间，因此采用BBF算法提高了搜索效率，降低了时间复杂度。

1.5 基于随机采样一致性算法的匹配筛选

对于上述基于亚像素角点提取的SIFT特征，再用BBF搜索算法进行候选匹配，此时仍然还存在比较多的错误和冗余匹配点，故文中采用随机采样一致性算法对候选匹配对进行筛选。

随机采样一致性算法，即RANSAC(RANdom SAmple Consensus)算法，是一种鲁棒的变换估计算法。它利用特征集合的内在几何约束关系进一步剔除错误的匹配[14]，其在SIFT特征筛选中的主要流程为：

(1)从候选匹配特征点样本集中随机抽选一个RANSAC样本，即n个匹配点对，实验中取n=4；

(2)根据这n个匹配点对计算两幅图像之间的变换矩阵H；

(3)根据特征点样本集、变换矩阵H和误差度量函数计算满足当前变换矩阵的一致集，并返回一致集中元素个数；

(4)根据当前一致集中元素个数判断是否最优(最大)一致集，若是则更新当前最优一致集;

(5)更新当前错误概率P，公式为：

P=(1-in_fracm)k

(6)

其中,in_frac是当前最优一致集中元素个数占样本总数的百分比；m是计算变换矩阵需要的最小特征点对个数，实验中取m=4；k是迭代次数。

若P大于允许的最小错误概率Pmin，则重复(1)至(4)继续迭代，直到当前错误概率P小于Pmin，实验中取Pmin=0.01，使匹配正确率达到99%。

2 实验研究

为测试文中所述匹配算法的实际应用性能，进行了专项实验进行验证。实验所采用的双目立体视觉系统包括2台1/3英寸SONYXC-ES50CECCD工业摄像机，2台ComputarM0814-MP2 8mm焦距镜头和大恒DHCG410图像采集卡。实验所采集的图像是一张8×8的正方形的棋盘格平面图样，其中每个正方形的尺寸为20mm×20mm。以下是对算法的实验验证与分析。

2.1 实验1：实时性与误匹配率分析

实验1的结果如图4(a)～(d)所示。

图4 实验1的匹配结果比较

其中，图4(a)和(b)给出了未经匹配筛选之前原SIFT算法与文中算法的匹配结果。其算法耗时、匹配正确率如表1所示。

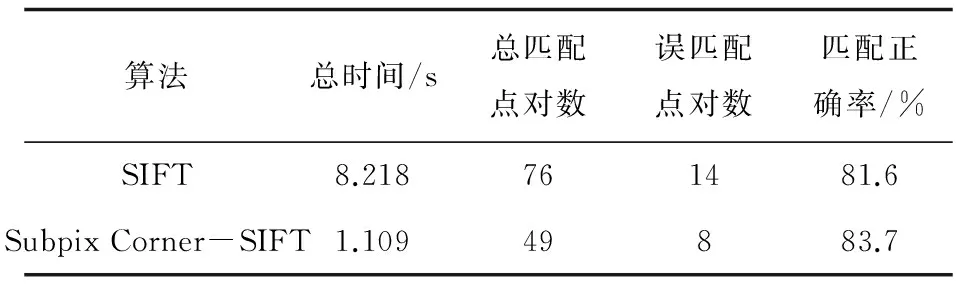
表1 SIFT算法与文中算法的比较(未筛选前)

由表1的结果表明，文中算法所得到的匹配点数量比原SIFT算法有所减少，耗时大大降低，从而节约了算法的匹配时间，加快了算法的匹配速度。匹配正确率都超过了80%，证明了算法的鲁棒性，但在未经过RANSAC算法筛选之前，仍有一定的错误匹配点对的存在。

筛选后的匹配图像如图4(c)和(d)所示，匹配点对数有所减少，如表2所示。

表2 RANSAC算法的筛选

由此可见，RANSAC筛选降低了误匹配率，使匹配结果更加精确。

2.2 实验2：精度分析

文中算法在Harris角点提取的基础上采用内插法将角点位置精度精确到亚像素级，以下通过棋盘格上的P1～P4(见图5)间的距离测试对算法精度进行分析。

图5 P1～P4的匹配

表3给出了测定的P1～P4在左、右摄像机的图像坐标；表4给出了距离测试结果。

从表4给出的距离测试结果可知,亚像素级角点提取进一步提高了匹配点对的位置精度，从而提高了整个算法精度，有利于在双目视觉系统中的实际应用。

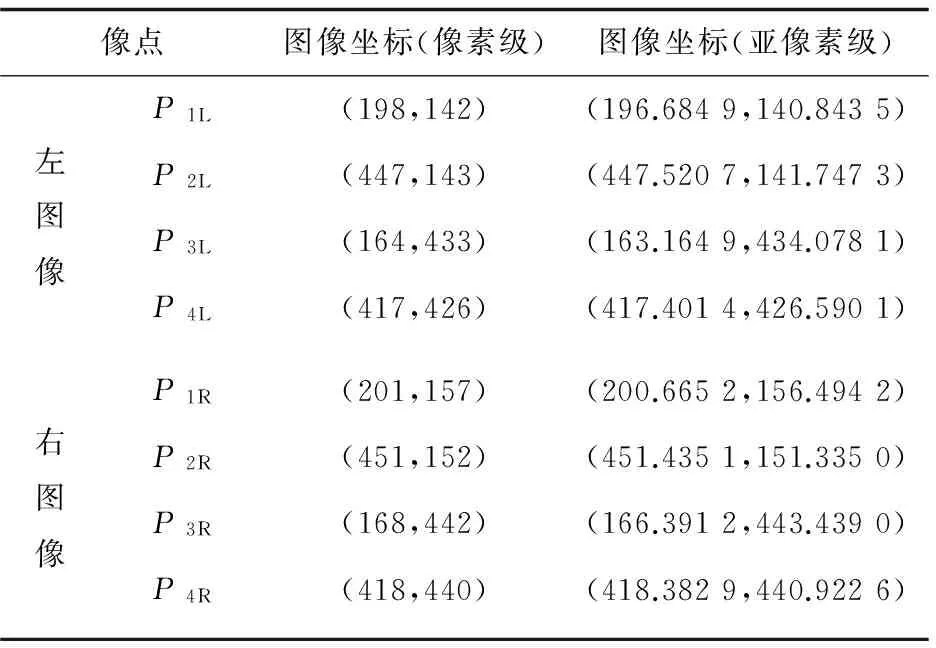
表3 P1～P4在左、右摄像机的图像坐标

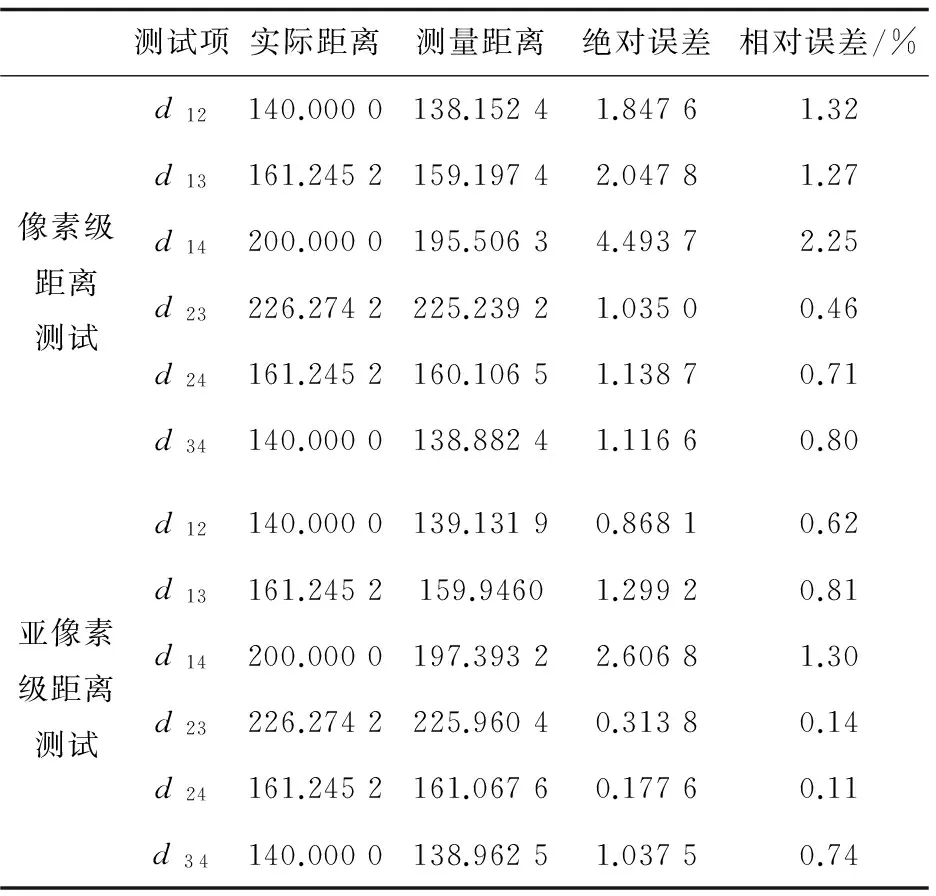
表4 像素级与亚像素级距离测试结果比较 mm

3 结束语

SIFT算法具有很好的尺度、旋转、视角和光照不变性，优于其他局部特征提取算子，但当应用于对实时性要求较高的双目视觉立体匹配时，该算法的复杂度较高、实时性较差，且其特征点不具备鲜明的几何特征，使算法的尺度不变特性优势难以体现出来。文中提出的基于亚像素角点的SIFT算法是对SIFT的一个成功改进，在保证SIFT算法鲁棒性的基础上，提高了匹配精度，降低了特征提取和特征匹配的复杂度，大大提高了算法的实时性。通过双目立体视觉匹配实验的结果验证了文中算法的有效性和实用性。

[1] 张广军.机器视觉[M].北京:科学出版社,2005.

[2] 高晓峰,史朝辉.一种改进的基于灰度投影的图像匹配算法[J].航空计算技术,2012,42(6):85-87.

[3] 曾 凯,王慧婷.基于区域灰度增强的种子特征匹配方法[J].中国农业大学学报,2013,18(5):136-140.

[4] 唐 烁,缪 源.基于Harris角点的图像匹配算法[J].微型机与应用,2013,32(2):41-43.

[5]LoweDG.Distinctiveimagefeaturefromscale-invariantkeypoints[J].InternationalJournalofComputerVision,2004,9(6):35-51.

[6] 齐乃新,曹立佳,杨小冈,等.基于方向约束的改进SIFT匹配算法[J].计算机科学,2014,41(6A):125-128.

[7] 赵钦君,赵东标,韦 虎.Harris-SIFT算法及其在双目立体视觉中的应用[J].电子科技大学学报,2010,39(4):546-550.

[8] 丁雄飞,张春燕.基于Moravec算子和改进的SIFT算法的图像匹配[J].合肥学院学报：自然科学版，2013,23(3):40-42.

[9] 龙忠杰,王吉芳,左云波.一种改进的Harris与SUSAN相结合的角点检测算法[J].计算机应用与软件,2013,30(12):133-136.

[10] 樊志华,王春鸿,饶长辉,等.基于Harris角点量与相位相关的亚像素级图像配准方法[J].计算机应用研究,2011,28(2):788-791.

[11] 布拉德斯基.学习OpenCV[M].北京:清华大学出版社,2009:353-355.

[12] 丁南南,刘艳滢,张 叶,等.基于SURF-DAISY算法和随机kd树的快速图像配准[J].光电子·激光,2012,23(7):1395-1402.

[13] 陈小丹,杜宇人,高秀斌.一种基于SURF的图像特征点快速匹配算法[J].扬州大学学报:自然科学版,2012,15(4):64-67.

[14] 王任华,霍宏涛,蒋 敏.RANSAC算法在同图复制鉴定中的应用研究[J].计算机应用研究,2014,31(7):2209-2212.

Research on a SIFT Stereo Matching Algorithm Based on Sub-pixel Corners

HONG Lei1,JI Bao-jian2,HONG Feng3

(1.School of Automotive and Rail Transit,Nanjing Institute of Technology,Nanjing 211167,China;2.College of Automation and Electrical Engineering,Nanjing University of Technology,Nanjing 211800,China;3.College of Electronic and Information Engineering,Nanjing University of Aeronautics &Astronautics,Nanjing 210016,China)

In view of the problems of the poor real-time performance,mismatching and no distinct geometric characteristics points on stereo matching application based on the Scale Invariant Feature Transform (SIFT) algorithm,present a new SIFT stereo matching algorithm based on sub-pixel corners.At first,the image corners are extracted and located in sub pixel coordinates by fitting interpolation method.Then the feature descriptors are established by the field gradient image histogram information structure based on the statistical information for the corners.Finally,the symmetrical characteristic similarity is measured and random sample consensus algorithm is used to achieve ultimate matching points.Experiments show that the proposed algorithm based on strong robustness,can greatly improve the real-time performance and the matching precision.

stereo matching;sub-pixel corner;SIFT;machine vision

2015-03-29

2015-07-01

时间：2015-11-19

江苏省产学研联合创新资金研究项目(BY2014005-09)；南京工程学院科研基金项目(YKJ201333)

洪 磊(1982-),男,博士,讲师,研究方向为机器视觉技术、轨道车辆微机控制技术。

http://www.cnki.net/kcms/detail/61.1450.TP.20151119.1113.074.html

TP391.41

A

1673-629X(2016)01-0048-05

10.3969/j.issn.1673-629X.2016.01.010