专家引领下的国培师资培训心得

⌾耿茂沂

专家引领下的国培师资培训心得

⌾耿茂沂

为了进一步强化教育教学理论的学习，加强对学科前沿信息的认知，更加深入的领会新课改的精神和内涵，我有幸远赴重庆西南大学，参加为期一个月的教师培训“国培计划”。

培训的主要内容有大学教授专题讲座、当地中学名师专题讲座、以及赴知名高中学现场观摩公开课。理论与实践相结合，培训内容安排科学合理，受益匪浅，专家讲座内容丰富、形式多样、主题鲜明，例如涉及教师伦理与师德师风建设、高中数学标准解读、教师压力管理与心理健康等诸多方面。

重庆师范大学黄翔老师就高中数学新课标的新变化以及修订的分析讲解，强调现在的两基(基础知识、基本技能)逐步走向四基(基础知识、基本技能、基本思想方法、基本活动经验)，这就要求教师在教学中更加注重教学活动设计，使教学活动尽量生活化、合理化、具有较高实用价值，以促进学生积极性，让学生“做数学、动手做、做中学”。

冯维教授讲授的主题是《教师积极心态的建设》，让我深刻的认识到教师面临着来自自身、学校、家庭、家长各方面的压力，教师必须学会采取行动缓解心理压力，减少不良情绪，其实快乐与痛苦完全由自己决定，贪婪夺走阳光心态，攀比源自不知足，正确对待名利得失，改变非理性认知，形成积极心态，才能从根本上获得心灵自由与幸福。专家讲座主题突出，实用性强，带给我全新的教学视野，进一步提高了自身教学素养。

“穷则独善其身，达则兼善天下”，故名重庆兼善中学，我有幸来此观摩公开课，厚重的文化底蕴和幽美的校园环境是学校的一大特色。公开课由该校青年教师周老师主讲，课题是：“不等式解法之饮水思源”，饮水思源源于古代庚信的《徽调曲》，“落其实者思其树，饮其流者怀其源”，数学解题方法与文学名句结合，题目新颖，耐人寻味。此方法是通过一道例题引出的。

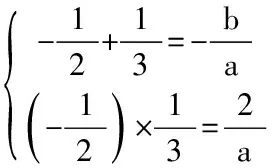
解得：a=-12,b=-2，

代入不等式2x2+bx+a<0

即：2x2-2x-12<0

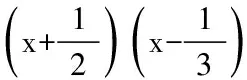
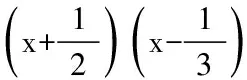
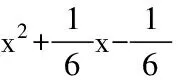
即：-12x2-2x+2>0

结合ax2+bx+2>0，对应系数a=-12,b=-2。

代入不等式2x2+bx+a<0

即：2x2-2x-12<0

饮水思源法本质上讲是一种数学常见的逆向思维，但用古语表达更加学生好奇心和求知欲，这节别具特色的公开课，蕴含浓郁的文化气息，巧妙的赢得在场的所有老师和同学的一致好评。

按照培训安排，我有幸来到云雾缭绕，山峦起伏的重庆西藏中学，特色鲜明的藏式建筑，一流的办学条件，培育了一批又一批来自雪域高原的莘莘学子，作为内地西藏班的名牌学校，自然也有着别具特色的教学理念和管理制度，值得我去学习和借鉴，公开课由教学经验丰富的高三年级张老师主讲，课题是：“三角函数模块复习”，看似很普通的一节课，教学方式却很新颖，采用小组讨论式教学模式。一进教室，所有学生六人一组，共分为六组，每组设组长一名，每组均包含成绩优秀的学生，带动成绩较差的学生，实现共同进步。首先由老师提出问题，各小组自主探究，并得出结论，然后每组指派一名小组代表上黑板讲解，学生讲解环节让在座的老师很是意外，学生站在讲台上丝毫没有胆怯，表现非常大方，信心满满，条理清楚，头头是道。当讲解正确合理，随即给该组记分，据校方说这样的积分是学生评优的参考，因此学生积极性相当高，课堂气氛异常活跃，一题多种解法频频出现，学生思维很灵活，之后由老师点评每种方法的优劣。整节课学生一直在思考，每个小组共同探讨，培养了学生良好的团队协作能力，达到了扶中帮困的效果，实实在在的体现了以学生为主体，教师充当引领和总结的角色。下课后组织座谈会，校领导称全校均采取小组讨论教学模式，已经实行了好几年，效果非常好，成绩综合排名已经位于重庆当地前列。

为期一个月的培训，既有丰富的理论学习，又有实用的课堂观摩，理论与实践形结合，既有观念的洗礼，也有理论的提升。既有新知识的积淀，也有教学手法的拓展，达到了预期的培训目的。我将以此为契机，不断进行深入的学习，不断丰富、完善、提升自己，让培训的硕果在平时的教学工作中大放光彩。

西藏民族大学附属中学 712000)