教好“因式分解”的体会

⌾ 唐朝晖

教好“因式分解”的体会

⌾ 唐朝晖

因式分解在中学数学中有着十分重要的地位，因此必须使学生能够熟练正确地进行多项式的因式分解。怎样教好“因式分解”这一章，我的体会是要着重抓好以下几个方面：

一、运用类比、对比的方法讲清因式分解的意义，使学生正确理解什么是分解因式

正确理解因式分解的意义是学好因式分解的前提。教材中指出“把一个多项式化为几个整式的积的形式叫做多项式的因式分解”。这就是说，分解因式就是把一个多项式化为单项式与多项式，或多项式与多项式的乘积的形式的过程。初一学生刚刚学习因式分解时，不少人常常把“a2-ab+b2=a(a-b)+b2”当成因式分解，或者混淆乘法运算与因式分解的区别。如何帮助学生明确因式分解的意义呢？

我的做法是：①通过与算术中的因式分解进行类比，引出代数中的因式分解，在类比中使学生掌握新概念。首先从“6=2×3”出发，引导学生回忆在算术中，把一个整数化为几个整数的积的形式叫做因式分解，从而类比：“a2-b2=(a+b)(a-b)”，启发学生说出多项式因式分解的意义。这样，使学生容易懂得什么是多项式的因式分解，加深他们的理解，又可防止将“a2- ab +b2= a(a-b)+ b2”(类比：29=4×7+1)误认为是因式分解的错误。②通过对比“(a+b)(a-b)= a2-b2”与“a2-b2=(a+b)(a-b)”使学生认识乘法运算与因式分解的联系，分清它们之间的区别，进一步明确因式分解的意义。不少学生在学习因式分解时，常易发生类似“y4-8y=y(y3-8)= y(y-2)(y2+2 y +2)=( y2-2y)(y2+2y+2)”的错误，这说明他们混淆了乘法运算与因式分解的区别。因此，教学中注意把因式分解与乘法运算进行对比，有着重要的意义。③通过辨别正确与错误的练习，防止学生“先入为主”地形成错误的概念，加深学生对正确概念的理解。

当然，学生对于因式分解的概念不是也不可能是一次就能真正理解的，我们既要重视第一次概念课的教学，又要在以后解各类因式分解的习题中逐步帮助学生理解因式分解的意义。

二、坚持由浅入深，循序渐进的原则，使学生逐步学会解各类因式分解的习题

学生学习新的东西，正确理解基础知识都有一个由浅入深、由具体到抽象、由特殊到一般的认识过程。为此，我们在教学中必须从最基本的入学，逐步过渡到比较复杂的和带有综合性的问题，那种操之过急的做法，只会使学生囫囵吞枣，结果是欲速则不达。

我们以应用平方差公式“a2-b2=(a+b)(a-b)”分解因式为例。教材中先举出了x2-16的例子，这里a、b都是单一字母或整数；接着 9m2-4n2=(3m)2-(2n)2，a、b都是系数为整数的单项式；

m2-0.01 n2=(m)2-(0.1n)2，a、b 都是单项式，系统出现了分数或小数；进一步，又安排了 (x+p)2-(x+q)2，16(a-b)2-9(a+b)2等a、b都是多项式的例子。在练习和习题中、复习题中，教材也注意了由浅入深的原则，逐步出现了

(a+b+c)2-(a+b-c)2，81a4-b4， 3ax2-3ay4，

(a-b)n+2-(a-b)n，(a2+b2-1)2-4a2b2，……

等习题，坚持从简单到复杂的安排例、习题，逐步说明公式的使用方法，使学生打好坚实的基础，有利于他们今后的学习。

三、加强学生使用字母的能力的训练

用数学知识解决实际问题，就必须善于把实际问题抽象为数学问题，而数学问题又经常用字母和符号来表达。初一学生刚刚用字母表示数，他们还不习惯于字母表示式子，对字母的使用能力还不强。因此，在因式分解的教学中要注意训练学生使用字母的能力，为今后进一步用式子述打下基础。

四、注意培养学生掌握一些处理问题的方法，提高分析问题和解决问题的能力

因式分解的教学中，在讲了四种基本方法以后，应结合综合性训练帮助学生归纳出把不念旧恶多项式分解因式的大致思考步骤，要使学生对于先考虑什么，后考虑什么，从哪几方面考虑，怎样作具体的分析有一个大致的轮廓。

一般说来，把一个多项式分解因式，首先考虑提取公因式，然后再考虑其它的方法。这里应该注意：如果有些项是分数系数，不便于观察时，我们可以应用通分(或撮一个分数公因式)的方法，将各项系数化为整数系数，例如：

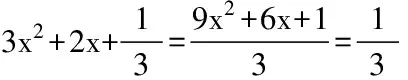
然后进行因式分解。

提取公因式后，往往是根据项数的多少来考虑因式分解的方法。在教学中，我的体会是：①对于二项式，首先考虑应用平方差、立方和(差)公式，对于某些双二次或其它特殊类型的，也可采用配方法。例如：x4+64=(x4+16x2+64)-16x2。②对于三项式，则考虑运用完全平方公式、十字相乘法或配方法、拆项添项法。例如x3-7x+6=(x3-x)-(6x-6)或者x3-7x+6=(x3-x2)+(x2-7x+6)在应用拆项添项方法时，一般应注意：多项式按降幂排列；最高次项不变，第二项系数必须是常项的约数；如果拆项添项后成为偶数项，分组分解时，或考虑用公式法，或考虑第一、第二项、第三、四项，……的系数比应该相等。④对于四项式，由于学生还未学习完全立方公式，所以主要用分组分解法。四项式的分组，不外二、二分组或一、三分组，对于二、二分组的主要考虑用提公因式法或公式法。例如：

xy+yz+xz+x2=(xy+yz)+(xz+x2)=y(x+z)+x(x+z)

=(x+z)·(x+y)

b3-b2-a3+a2=(a2-b2)-(a3-b3)

=(a+b)(a-b)-(a-b)(a2+ab+b2)

=(a-b)(a+b+a2+ab+b2)

对于一、三分组的，多用公式法。⑤对于五项式或五项以上的多项式，一般应考虑用分组分解，但要注意某此特殊多项式的分解方法。例如：

a2+b2+c2+2ab+2bc+2ca=(a+b+c)2,

x2-xy-2y2+4x-5y+3=(x-2y)(x+y)+(4x-5y)+3=(x-2y+1)(x+y+3),

等等。

总之，在因式分解的教学中，学生掌握了一般方法和规律后，老师要严格要求他们多练、反复练，使学生做到举一反三，熟能生巧，对于一般分解因式的习题能够一目了然，很快写出结果，为以后的学习打下坚实的基础。

湖北省荆州市少年儿童体育学校 434000)