地震差动下边界-地基-斜拉桥体系破坏特征

柳国环，　练继建，　燕　翔，　刘　伟

(1. 天津大学　a.建筑工程学院； b.水利工程仿真与安全国家重点实验室， 天津　300072；

2. 燕山大学　土木工程学院， 河北　秦皇岛　066004)



地震差动下边界-地基-斜拉桥体系破坏特征

柳国环1，练继建1，燕翔1，刘伟2

(1. 天津大学a.建筑工程学院； b.水利工程仿真与安全国家重点实验室， 天津300072；

2. 燕山大学土木工程学院， 河北秦皇岛066004)

摘要：同时考虑边界条件和地基-结构相互作用对大跨桥梁结构地震响应的影响是个复杂问题。本文以一大跨斜拉桥为例，通过开发的系列程序建立了边界-地基-桩-斜拉桥结构的ABAQUS模型，生成了目标场地多点地震动，对比了不同地基边界条件对大跨斜拉桥结构自振特性的影响，探讨了地表/地下多点地震动作用下、不同地基边界条件对大跨斜拉桥体系弹塑性发展过程及倒塌模式的影响规律。结果表明：(1)进行大跨斜拉桥结构的抗震分析时，有必要考虑地基边界条件的影响；(2)地表多点地震动输入下，考虑地基-结构相互作用时，大跨斜拉桥结构的弹塑性发展过程和倒塌模式与单独斜拉桥不同；(3)粘弹性人工边界条件考虑了周围土体对地基的作用，地基相对变形较小，对上部斜拉桥结构起到了一定的保护作用。

关键词：大跨斜拉桥；边界-地基-结构相互作用；多点地震动；弹塑性分析；倒塌分析

Elasto-plasticity Analysis and Failure Characteristics of

对于大跨度桥梁结构而言，通过数值分析事先了解其在大震和超大震作用下的弹塑性及抗倒塌性能，是进一步保障桥梁结构工程运营期间安全服役的一条有效途径。地震作用下各桥墩/台输入的地震动存在较大的差异，不同边界条件的地基也会影响桥梁结构在地震作用下的响应[1]。因此，进行数值分析时，不仅要考虑地基与桥梁结构的相互作用，同时还应考虑地基边界条件对结构地震响应的影响。

但是，在大跨度桥梁结构的地震弹塑性和倒塌分析中，已有的研究很少既考虑地基-结构的相互作用又考虑边界条件的影响，而弄清楚边界-地基-桥梁结构体系的地震响应是进行结构抗震设计与分析的基础，所以有必要对这一问题进行详细分析。具体研究思路为：首先，运用开发的TJU.SAP2ABAQUS接口程序[2～4]，建立了用于数值分析的ABAQUS斜拉桥体系有限元模型，并且在模型中考虑了桥梁构件中钢筋和混凝土材料的非线性滞回效应[5,6]。随后，对转化前、后的模型进行模态分析，考察了不同边界条件下斜拉桥结构体系(包括单独斜拉桥和固定边界-地基-斜拉桥与粘弹性人工边界-地基-斜拉桥)的自振特性，为后续的结构地震反应分析奠定基础。然后，基于地表功率谱的多点地震动可视化程序[4]，开发了地表多点地震动模拟程序MEGMS和地下多点地震动模拟程序MEUMS，根据实际情况生成目标场地对应地基位置的多点地震动[7,8]。最后，对不同边界地基-桩-斜拉桥结构体系在地表/地下多点地震动激励下，进行大震、超大震作用下的弹塑性和倒塌分析。

本文以一大跨斜拉桥结构为例，通过开发的系列程序构建了边界-地基-桩-斜拉桥结构模型，对比了不同地基边界条件对大跨斜拉桥结构自振特性的影响，提出了一种更加实用的粘弹性人工边界模型地震输入的高效加载方法，探讨了地表/地下多点地震动作用下、不同地基边界条件对大跨斜拉桥体系弹塑性发展过程及倒塌模式的影响规律。

1数值模型与模态分析

1.1模型建立与一致性检验

图1　地基-桩-斜拉桥SAP2000模型生成和ABAQUS模型转化

某跨海大桥为双索面双塔斜拉桥，整桥全长765 m，主跨423 m，桥面至桥墩底部高度为46.5 m，斜拉桥两岸各设一座150 m高的折线“H”型钢筋混凝土桥塔，桥塔两端分别用22对斜拉索与桥面连接，斜拉索呈扇形分布。桩基础直径为2.2 m，沿周边布置48根直径为40 mm的HRB400级钢筋，地基土直径为11 m，利用开发的Foundation2013程序生成分层地基及钢筋混凝土桩基础的SAP2000有限元模型，如图1(a)所示。斜拉桥箱型主梁高1.380 m，材料为C60混凝土；桥塔高150 m，材料为C50混凝土；桥面板现浇层采用C40混凝土；斜拉索采用带PE环氧涂层的钢绞线，抗拉强度标准值为1860 MPa，斜拉桥的SAP2000有限元模型如图1(b)所示。将建好的上部斜拉桥SAP2000模型与所生成的地基及基础模型合并，形成地基-桩-斜拉桥的SAP2000整体有限元模型，如图1(c)所示。利用开发的接口程序TJU.SAP2ABAQUS将SAP2000整体模型转化为地基-桩-斜拉桥的ABAQUS模型，如图1(d)所示。从模型转化前、后的对比图中可以看出，桥墩、桥塔、桥面板、斜拉索等部件的形状与尺寸完全一致。由此说明，开发的TJU.SAP2ABAQUS接口程序具有较好的转换精度与可靠性。1.2地基边界对斜拉桥自振特性的影响

本节通过对比单独斜拉桥模型、固定边界地基-桩-斜拉桥模型和粘弹性人工边界地基-桩-斜拉桥模型的模态分析结果，考察不同边界条件地基对斜拉桥动力特性的影响。其中，后两种斜拉桥模型又各分为两类，即桩-土固结和桩-土摩擦模型。由于本文主要考虑纵向地震作用，故重点关注斜拉桥的纵向模态。表1给出了不同边界条件的地基-桩-斜拉桥模型纵向自振频率对比情况。从表中可以看出，不同边界条件地基-桩-斜拉桥模型的频率有所差别，其频率关系为“斜拉桥>地基-桩-斜拉桥(固定边界)>地基-桩-斜拉桥(粘弹性人工边界)”，并且低阶振型对应的频率差别较大，高阶振型对应的频率差别较小，其原因在于：不考虑地基时，斜拉桥底部为固定约束；考虑固定边界地基时，斜拉桥基础与土体弹性接触，但土体与边界固定约束；考虑粘弹性人工边界地基时，斜拉桥基础与土体弹性接触，并且土体与边界弹性接触。因此，斜拉桥在地基边界上的刚度表现为：“斜拉桥>地基-桩-斜拉桥(固定边界)>地基-桩-斜拉桥(粘弹性人工边界)”，从而在频率上的表现为：“斜拉桥>地基-桩-斜拉桥(固定边界)>地基-桩-斜拉桥(粘弹性人工边界)”。

从表中可以看出，是否考虑桩-土摩擦对地基-桩-斜拉桥模型的自振频率影响不大，所以图2中仅给出了与表1中频率相对应的斜拉桥模型与桩-土固接(固定边界和粘弹性人工边界)斜拉桥模型的振型对比情况。从图中可以看出，考虑固定边界时，地基-桩-斜拉桥结构的自振频率较单独斜拉桥模型变化较大，尽管两种模型的各阶振型也有一定的改变，但总体相似程度较高；考虑粘弹性人工边界时，地基-桩-斜拉桥结构的自振频率较单独斜拉桥模型变化也较大，两种模型的一阶振型相似度较高，但高阶振型相差较大，与固定边界模型相比，考虑粘弹性人工边界的地基模型对斜拉桥自振频率与振型的影响更为显著。因此，进行大跨斜拉桥结构的抗震计算时，有必要考虑地基边界条件的影响，否则将会对分析结果造成较大误差。

表1　不同斜拉桥模型纵向自振频率比较

图2　不同斜拉桥模型纵向模态振型比较

2地表与地下多点地震动

2.1地表多点地震动生成与验证

结合本文的长周期大跨斜拉桥结构，选定目标功率谱为可考虑低频分量的Clough-Penzien修正白噪声模型[9]，其功率谱密度函数为

S(ω)=S0=

(1)

式中：S0为谱强度因子；ω为圆频率；ωg和ζg分别为场地的卓越频率和阻尼比；ωf和ζf分别为模拟地震动低频分量能量变化的参数。

不同特征的场地土环境、土壤条件及地震动，所得到的相干函数不同。综合考虑，本文采用描述百米级区域效果较好的Hao相干模型[10]，其表达式为

(2)

(3)

图3　地表多点地震动时程

图4　模拟功率谱与目标谱比较

图5　相干函数模拟值与目标值比较

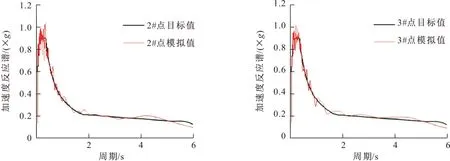
图6　模拟加速度反应谱与规范反应谱比较

式中：γjk(w,d)是j和k两位置间的相干函数；a1(ω)为圆频率ω相关的函数；d为j、k的空间距离；β1、a、b和c为常数。综合上述因素，并考虑计算工作的方便，开发了地表多点地震动软件MEGMS进行多点地震动时程模拟。根据所需目标点，共生成6条地震波，其时程曲线如图3所示。由于篇幅所限，本文仅给出部分比较结果。图4比较了目标点1#与5#处的地震动时程曲线模拟功率谱与目标功率谱。图5比较了目标点1#与5#以及目标点4#与5#处模拟的地震动加速度时程曲线相干函数与目标相干函数。图6比较了目标点2#与3#处模拟的地震动加速度反应谱与JTJ 213-98《海港水文规范》[11]加速度反应谱的拟合结果。从这些图中可以看出，模拟生成的地表各目标点位置的多点地震动功率谱、空间相干性以及反应谱均与理论值吻合较好。2.2地下多点地震动生成与特性

本文将斜拉桥地基中的土体分为三层，各层土体的具体参数如表2所示。考虑多点地震动与地震动的传播规律，根据土体属性，利用开发的地下多点地震动软件MEUMS，得到不同目标点的地下多点地震动(每个地基自底向上生成四条地震动)，如图7所示。由于篇幅所限，本文仅给出1#地基各层土体的地震动时程及相应的频谱，分别如图8、9所示。从图中可以看出，模拟生成的地基各土层地震动差异显著，即加速度幅值表现为“地表>一层>二层>三层”，而卓越频率则表现为“地表<一层<二层<三层”。其原因在于：地基土体刚度表现为“上软下硬”，从而导致地震动幅值自下而上逐渐放大，而各土层的主频自下而上逐渐减小。

表2　地基各土层参数

图7　地基属性及地震动输入示意/m　

图8　1#地基不同土层地震动时程　

图9　1#地基不同土层地震动傅里叶谱

3边界-地基-桩-斜拉桥地震反应分析

3.1斜拉桥与地基-桩-斜拉桥模型地震反应

选取如图10所示位置为观测点，图11给出了不同峰值地震加速度下，独立斜拉桥模型与地基-桩-斜拉桥模型同一观测点的位移反应对比情况。需要说明的是，本节所述两模型输入的地震动均为2.1节生成的地表地震动(包括地基地震动的输入)。从图中可以看出，无论地震动峰值大小，地基-桩-斜拉桥模型的观测点位移均大于独立斜拉桥模型，且比例达6～8倍，其原因可解释为：相较独立斜拉桥模型而言，地基-桩-斜拉桥模型的频率均偏低，模态排列也更为密集，这就使得地基-桩-斜拉桥模型中进入地震谱带的共振频率更多，从而使结构反应更为强烈。

3.2斜拉桥与地基-桩-斜拉桥模型倒塌模式

图12和图13分别给出了斜拉桥模型和地基-桩-斜拉桥模型的倒塌过程。从图中可以看出，地基-桩-斜拉桥模型倒塌速度(12 s)快于斜拉桥模型(14 s)。倒塌过程中，斜拉桥模型两侧的桥墩与桥塔的扭摆方向相反，而地基-桩-斜拉桥模型两侧的桥墩与桥塔同方向倒塌。造成上述现象的原因主要有两点：(1) 如1.2节所述，地基-桩-斜拉桥模型纵向模态分布更为密集，进入地震谱带的共振频率更多，从而引起的地震反应也更剧烈；(2) 地基-桩-斜拉桥模型中，桥墩底部为梁单元，地基则为实体单元，桥墩底部与基础连接，地震时桥墩底部的梁单元相对地基实体单元会发生塑性大转角，故地基-桩-斜拉桥模型倒塌过程快。而且，若发生同向转角，桥墩与桥塔即发生快速同向倒塌趋势；相反，不考虑地基的斜拉桥模型，桥墩底部与基础固接，地震过程中桥墩底部单元无大转角，故倒塌过程较慢。

图10　桥墩观测点

图11　不同峰值加速度下斜拉桥模型与地基-桩-斜拉桥模型观测点反应对比

图12　斜拉桥模型倒塌模式

图13　地基-桩-斜拉桥模型倒塌模式

由此可见，地基起到了弱化结构抗震性能的负作用。然而，传统的分析方法基本不考虑地基的影响，而是人为将桥墩底部约束设定为“固接”形式，这显然与实际情况并不相符。因此，对此类大跨斜拉桥结构抗震分析，有必要考虑地基的影响，否则将导致结果偏于不安全。3.3不同边界-地基-桩-斜拉桥体系弹塑性分析

3.3.1粘弹性人工边界地震输入的高效加载途径

对粘弹性人工透射边界模型，地震波的输入包括三项内容：(1) 刚度力；(2) 阻尼力；(3) 节点反力。

对于多层地基土而言，同一层土体各节点的切向或法向刚度(或阻尼)数值均相同。但是，由于各节点运动方向(速度、位移)为某一线性方向，所以各节点实际的刚度(或阻尼)为其切向分量与法向分量在该方向上的分量之和，如图14所示。

图14　圆形地基节点的刚度、阻尼分量分解

对于圆形地基土，第i层土第j个节点的刚度系数Kij为：

Kij=Kσ,i·cosθj+Kτ,i·sinθj

(4)

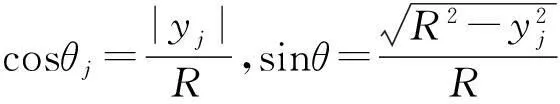
由此，第i层土第j个节点的刚度力FK,ij为：

FK,ij(t)=Kijui(t)

(5)

同理，第i层土第j个节点的阻尼力FC,ij为：

FC,ij(t)=Cijvi(t)

(6)

式中：Kσ,i和Kτ,i分别为第i层土体法向刚度系数与切向刚度系数；Cσ,i和Cτ,i分别为第i层土体法向阻尼系数与切向阻尼系数；R为地基直径；yj为节点j与地基圆心Y向位移；ui(t)和vi(t)分别为第i层土体的位移与速度。

从式(5)和式(6)可以看出，无论刚度力或阻尼力，其大小均与yj有关，说明土体的刚度力与阻尼力仅与节点位置有关。那么，上述荷载的施加采用GUI中的“场函数”功能即可完成。

粘弹性人工透射边界模型中，节点反力数据采用固定边界模型的计算结果。由于GUI不具备单个数据(单节点、单方向)的自动输出能力，若采用手动输入方法，工作量大，且易发生错误。因此，可先利用ABAQUS-REPORT功能输出所有反力的整体文件，随后利用其他工具将其分割为单个数据进行加载。

图15　节点反力处理程序

本文利用MATLAB开发了反力分割处理工具(如图15所示)，该程序可以将固定边界条件下各节点反力的时程数据提取出来，并按节点分割成单个节点反力幅值文件，同时可以按照ABAQUS语法规则生成调用这些幅值文件的INP格式反力加载语句。

3.3.2不同边界条件下结构弹塑性反应比较

图16　固定边界与粘弹性人工边界模型观测点位移反应

利用开发的MEUMS软件模拟不同目标点的地下多点地震动，并将地震动的峰值加速度分别调整为0.2g，0.4g和0.6g，地基土分层情况与地震动输入方法如2.2节所述。选取桥塔顶点为观测点，不同峰值加速度下观测点的位移时程如图16所示。从图中可以看到，随着地震波峰值的增加，地面运动不断加剧，固定边界与粘弹性人工边界条件下观测点的峰值位移均增加。但是，粘弹性人工边界条件下观测点的位移反应要小于固定边界条件下的情况，并且位移时程曲线也相对和缓，其原因在于：粘弹性人工边界条件下，地基运动受到周围土体的限制，相当于在地基周围均匀添加了一圈弹簧和阻尼器，其中阻尼器消耗部分地震能量，起到了减轻结构地震反应的作用。同时，从1.2节的分析可知，粘弹性人工边界基础-桩-斜拉桥模型的自振周期比固定边界基础-桩-斜拉桥模型的周期长，并且远离地震动的卓越周期。因此，粘弹性人工边界条件下观测点的位移反应较小。但是，随着地震波峰值加速度的增加，两种边界条件下观测点的最大位移反应的差距逐渐减小。由此可见，粘弹性人工边界考虑了周围土体对地基变形的限制作用，这对结构抗震是有利的，也与实际情况更符合。因此，进行大跨桥梁结构的抗震研究时，考虑粘弹性人工边界条件较固定边界条件更为合理。3.4边界条件对地基-桩-斜拉桥体系破坏模式的影响

本节考察不同边界条件对斜拉桥体系破坏模式的影响，分析时对不同边界条件的斜拉桥体系进行地下多点地震动输入，并将地震动峰值加速度调整为5g。

图17　固定边界地基-桩-斜拉桥模型倒塌模式

图18　粘弹性人工边界地基-桩-斜拉桥模型倒塌模式

图17给出了固定边界地基-桩-斜拉桥模型的破坏倒塌过程。从图中可以看出，固定边界条件下，斜拉桥模型的破坏倒塌过程主要分为四个阶段，即：(1) 地震作用开始阶段，对斜拉桥结构输入地下多点地震动，各层地基土的运动存在差异较大。此时，在剪力作用下地基和基础首先发生较大塑性变形 (图17 a)；(2) 随着地震作用的持续以及地基变形的进一步发展，各桥墩的相对变形逐渐增大，桥面发生扭曲变形 (图17 b)；(3) 桥面严重扭曲并向一侧漂移，迫使桥墩发生较大的同向塑性转角 (图17 c)；(4) 随着地震动持续时间的进一步增加，塑性破坏蔓延至整个桥体，桥塔也发生严重弯曲，桥梁两侧桥墩倒向一侧，整个桥体发生倒塌 (图17 d)。图18给出了粘弹性人工边界地基-桩-斜拉桥模型的破坏倒塌过程。同样，粘弹性人工边界下，斜拉桥体系的破坏倒塌过程也可以分为四个阶段，即：(1) 地震作用的开始阶段，在剪力作用下，桥墩位置首先出现塑性变形 (图18 a)；(2) 随着地震作用的持续，桥梁两侧的桥墩发生较大转角，但与固定边界地基的情况不同，桥墩转角并非同一方向 (图18 b)；(3) 桥面发生严重扭曲，但与固定边界地基不同的是，一侧桥墩和桥塔弯曲变形严重，而另一侧桥墩和桥塔未出现大变形 (图18 c)；(4) 随着地震作用的进一步增加，桥面向一侧漂移，致使一侧桥墩和桥塔倒塌，另一侧桥墩和桥塔发生较大变形，整个斜拉桥结构并未全部发生倒塌 (图18 d)。

对比固定边界和粘弹性人工边界条件下斜拉桥体系的倒塌破坏过程可以看出，地基-桩-斜拉桥的破坏模式具有如下特点：(1) 两种边界条件下桥体的倒塌方向一致，其原因在于两种模型的地震动输入相同，区别仅在于粘弹性人工边界条件下附加了弹簧力和阻尼力，而这两种力都是被动力，分别与地基的位移和速度方向相反，并不能改变地震动的整体走向，因此人工边界条件下桥体倒塌方向与固定边界模型一致；(2) 地基变形差异较大，固定边界下地基各层土体的相对变形严重，从第一阶段开始，地基一直保持着较大的相对变形；与此不同的是，人工边界条件下，地基自始至终未发生如此大的相对变形，原因在于：粘弹性人工边界条件下，考虑了周围土体对地基的嵌固作用(地基周围均布弹簧和阻尼器)，地基相对变形较小；(3) 结构倒塌方式不同，具体表现为：固定边界条件下，桥体沿着桥面漂移方向倒向一侧，两侧桥墩和桥塔均被压垮；人工边界条件下，一侧桥墩和桥塔被压垮，另一侧桥墩桥塔并未倒塌，整个桥梁呈现一种半倒塌模式，其原因主要是：人工边界条件下，地基周围引入了弹簧和阻尼器，阻尼力消耗了地震输入的部分能量，对上部结构起到了一定程度的保护作用。

从以上两种边界条件下斜拉桥的倒塌过程不难看出，斜拉桥体系的薄弱环节均出现在桥墩与地基的接触部位，而倒塌过程也都是从桥墩与地基之间出现相对转角开始，随后由于地震输入能量的增加，致使桥墩与地基间的相对转角逐渐增大，从而最终导致斜拉桥倒塌。

4结语

本文通过开发的系列程序构建了边界-地基-桩-斜拉桥结构模型，探讨了地表/地下多点地震动作用下、不同边界条件对大跨斜拉桥体系弹塑性反应及倒塌模式的影响，主要结论如下：

(1)结合实际工程，检验了开发的接口程序TJU.SAP2ABAQUS转化模型的实用性和准确性，同时与开发的地表多点地震动MEGMS与地下多点地震动MEUMS程序相结合，大大提高了直接在ABAQUS中分析复杂模型的效率。

(2)指出了地表多点地震动输入下，是否考虑边界条件对地基-桩-大跨斜拉桥结构弹塑性发展过程和倒塌模式的影响不同。与单独斜拉桥结构相比，考虑地基土时，大跨斜拉桥结构自振频率减小，模态频率更加密集，地震反应也更为强烈。由此说明，对于此类大跨斜拉桥结构的地震分析，有必要考虑地基边界条件的影响。

(3) 针对ABAQUS提出了一种更加实用的粘弹性人工边界模型地震输入的高效加载方法。地下多点地震动输入下，粘弹性人工边条件与固定边界条件对地基-桩-大跨斜拉桥结构地震弹塑性反应和倒塌模式的影响不同。与固定边界条件相比，粘弹性人工边界条件模型中考虑了周围土体对地基的作用，消耗了输入结构的部分能量，地基相对变形较小，从而对斜拉桥上部结构起到了一定程度的保护作用。

参考文献

[1]Kahan M, Gibert R J, Bard P Y. Influence of seismic waves spatial variability on bridges: a sensitivity analysis[J]. Earthquake Engineering and Structural Dynamics, 1996, 25(8): 795-814.

[2]柳国环, 练继建, 国巍. 结构动力弹塑性与倒塌分析(I)——滞回曲线改进、ABAQUS子程序开发与验证[J]. 地震研究, 2014, 37(1): 123-131.

[3]柳国环, 练继建, 国巍. 结构动力弹塑性与倒塌分析(II)——SAP2ABAQUS接口技术、开发与验证[J]. 地震研究, 2014, 37(1): 132-140.

[4]柳国环, 练继建, 孙雪艳, 等. 结构动力弹塑性和倒塌分析(III)——地震差动作用下输电塔—线体系的弹塑性与倒塌分析[J]. 地震研究, 2014, 37(1): 141-150.

[5]柳国环, 陆新征, 国巍, 等. 考虑地震动多点激励与材料应变率效应的主跨300 m级独塔斜拉桥弹塑性分析[J]. 计算力学学报, 2014, 31(4): 486-494.

[6]柳国环, 李宏男, 林海. 结构地震响应计算模型的比较与分析[J]. 工程力学, 2009, 26(2): 10-15.

[7]柳国环, 李宏男, 国巍. 求解结构地震响应位移输入模型存在的问题及其AMCE实效对策[J]. 计算力学学报, 2009, 26(6): 862-869.

[8]柳国环, 李宏男, 国巍, 等. 求解结构地震响应位移输入模型中存在问题的一种新解决方法[J]. 工程力学, 2010, 27(9): 55-62.

[9]Clough R W, Penzien J. Dynamics of Structure(3rd Edition)[M]. New York: McGraw-Hill In, 2003.

[10]Hao Hong, Oliveira C S, Penzien J. Multiple-station ground motion processing and simulation based on SMART-1 array data[J]. Nuclear Engineering and Design, 1989, 111(3): 293-310.

[11]JTJ 213-98. 海港水文规范[S].

Long-span Cable-stayed Bridge Considering Boundary-foundation Interaction

Under Multiple-support Seismic Excitations

LIUGuo-huan1,LIANJi-jian1,YANXiang1,LIUWei2

(1. a.School of Civil Engineering; b.State Key Laboratory Hydraulic Engineering Simulation and Safety,

Tianjin University, Tianjin 300072, China; 2. School of Civil Engineering and Mechanics,

Yanshan University, Qinhuangdao 066004, China)

Abstract:Seismic response effect of the long-span bridge structure considering both boundary condition and soil-structure interaction simultaneously is a complex problem. Taking a long-span cable-stayed bridge as an example, the boundary-foundation-pile-cable-stayed bridge model was established by a series of developed programs. The target site multi-support ground motions were also generated. The different boundary conditions on the vibration characteristics effect of the long-span cable-stayed bridge were compared. The effect of different boundary conditions on the elasto-plasticity development process and collapse mode of the long-span cable-stayed bridge was also discussed under surface/underground multi-support ground motions. The results indicate that: (1) It is necessary to consider the effect on the boundary conditions of the foundationin the seismic analysis of large-span cable-stayed structure; (2) When considering foundation-structure interaction, the elasto-plastic development process and collapse mode of the large-span cable-stayed bridgeare different with the single cable-stayed bridge under the surface multi-supportground motion; (3)Accounting forthe effect of soil surroundedby the foundationin the viscous-spring artificial boundary condition, the foundation deformation is relatively smallerand this plays a protective role in the upper cable-stayedstructure.

Key words：long-spancable-stayed bridge; boundary-foundation-structure interaction; multi-supportseismic excitations; elasto-plasticity analysis; collapse analysis

中图分类号：TU311.3; U442.5+5

文献标识码：A

文章编号：2095-0985(2016)01-0044-10

基金项目：国家自然科学基金(51408409)；中国博士后科学基金(2011M500332)；天津市应用基础与前沿技术研究计划(15JCQNJC07400)

作者简介：柳国环(1980-)，男，天津人，副教授，博士，研究方向为工程结构动力计算(Email：liugh@tju.edu.cn)

收稿日期：2015-10-19修回日期： 2015-11-03