返璞归真，追本溯源——谈“直线的相交”教学环节设计

⌾吴碧奕

(作者单位：浙江省温州市绣山中学 325000)

返璞归真，追本溯源
——谈“直线的相交”教学环节设计

⌾吴碧奕

数学最大的特点就是抽象，教学中以精妙的问题设计有效启发学生追求知识的本真，学生积极主动投入课堂学习中，让课堂的学习更加有效。

片断1：动手画画，开宗明旨

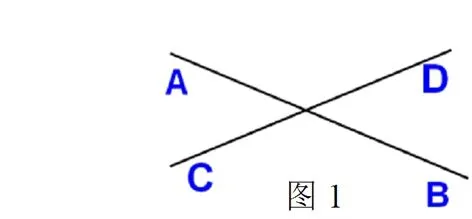
教师：请同学们在自己的积累本上先画一条直线AB，然后作一条直线CD与直线AB相交。

同时请一位同学画到黑板上，形成图1。

教师：你是根据什么判断这两条直线是相交的？

生1：只有一个交点。

师：这时候两条直线只有一个公共点，我们就称这两条直线相交，这个公共点就叫做交点。

同时教师将交点记为O，完成相交直线的概念的教学。

评析：

很多教师引入相交线的概念都是是利用立交桥的图片(如图3)或者十字路口的图片(如图4)。两条立交桥只能抽象成异面直线，根本不可能相交，而十字路口的道路这么宽，要抽象成直线是不是太牵强？这样的引入忽视了一个重要的事实，那就是学生在小学阶段就在大量的图片中认识了相交的直线，具备对直线这样抽象的概念的直观认识，教学中要善于利用学生已有的知识经验，尽管提倡数学源于生活，然而更要尊重学生已有的认知，学生能够画出正确的图形又能通过交点的个数判断，这就说明已经掌握了这个概念。学生已经懂的不用说，已经会的不用教，只需要简单的步骤帮助学生回忆提炼，再加以适当的点拨即可，这样的引入返璞归真，更有数学味，也更加有效。

片段2：寻找本质，思维拓展

师：如图5，过点O添一条直线EF，则图中有几对对顶角呢？请把它们找出来。

生1信心满满地走到黑板上画了起来，当他画出图6的时候，有一对对顶角怎么也找不出来了，在讲台上紧张地等着。

教师安慰他先回到座位，鼓励其他学生来帮忙，一位学生嘀咕了一句：“画的和蜘蛛网一样，看都看不清了。”

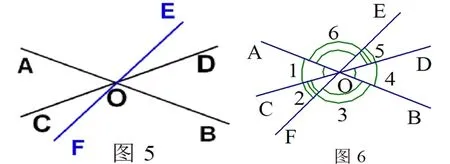
教师：确实，凌乱的图形确实不容易发现，能不能把图形进行分离，让图形变简单一点。

教师进一步点拨：请同学们回顾一下对顶角是怎么形成的？

生：两条相交的直线形成2对对顶角。

教师：我们不妨将图5分成两两相交的直线，能分出几对？

生2：能分出3对，AB与CD相交，AB与EF相交，CD与EF相交。(如图7)

教师：这样共有几对对顶角？

生3：共有6对对顶角。

教师：对顶角是由直线相交形成的，抓住这个本质，我们就能轻松解决这个问题了。

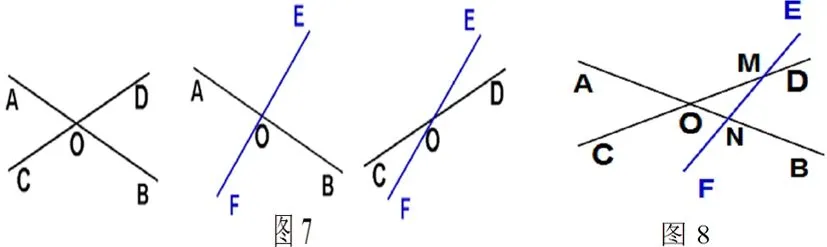
变式练习：如图8，已知直线AB，CD，EF分别相交于点O、M、N，则图中有几对对顶角?请把它们找出来.生4：有6对，在交点O处有两对，在交点M处有两对，在交点N处有两对，所以共有6对对顶角。

教师：同学们对比图5与图8，图形不同，对顶角的数量却是相同的，这是为什么呢？

生5：图5可以看作把图8中的3个交点重合在一起，所以不论交点个数是几个，3条直线两两相交都是6对对顶角。

师追问：平面内4条直线两两相交，有几对对顶角呢？

生6很快就举手了，“6+6=12！”

同学们都惊呼“你怎么这么快？”

生6：前面3条直线两两相交有6对对顶角，那么第4条直线要和前面3条直线都相交，不论交点重合不重合都会产生3个交点，所以又增加6对对顶角，总共12对。

生6话音刚落，教室里就想起了热烈的掌声。

师：非常好，这位同学抓住对顶角产生的本质是两条直线相交，所以只要数两两相交的直线有几对，就可以得到对顶角的数量。根据这种办法我们还可以继续探索平面内5条直线、6条直线、直至n条直线两两相交形成的对顶角的数量。这就作为今天的课外拓展问题。

评析：

在寻找数对顶角的数量时，教师不是急于揭示本质，而是让学生先经历迷茫和错误，当“蜘蛛网”状的图形出现后，学生体会到画图方法的局限性，这时候教师趁机抓住学生的心里特征，让学生去回顾对顶角的形成，追本溯源，由此想到将3条两两相交的直线分成3组，从而找到更优的方法。在寻找方法的过程中，让学生“历经艰难”，熟知其中的“沟沟坎坎”，必定对获得的新方法印象深刻。

学生是学习的主体，教师是教学的组织者和引导者，这个环节的设计很好地体现了这一点。教师设计了两个图5与图8的类比问题，引导学生解答、对比、思考，寻找这两个问题之间的本质联系，揭示方法，从而达到多题归一。从案例中我们可以看到学生经过思考对比，自己便能发现对顶角的数量与交点个数无关。此时教师不是急于探究4条直线、5条直线乃至n条直线的推广，而是课堂内的学习拓展到课外，激励学生继续研究数学，培养数学的探究精神。数学的教学少一分拔苗助长的功利，多一点静候花开的耐心，经过时间的酝酿，学生的数学学习定能开出美丽的花朵。

在这两个片段中，学生既经历了动手操作的切身体会，又感受了多题归一的辩证统一，既巩固了知识概念，又对方法有了哲学高度的理解，在解决问题的过程中真切感受到学习数学的乐趣。

(作者单位：浙江省温州市绣山中学 325000)