基于区间时间分配的列车速度曲线节能优化及其在CMC环境测试

蔡 虎，侯晓伟，张捷敏，杨 扬

（1.北京交通大学 电子信息工程学院，北京 100044；2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044）

基于区间时间分配的列车速度曲线节能优化及其在CMC环境测试

蔡 虎1，侯晓伟2，张捷敏2，杨 扬2

（1.北京交通大学 电子信息工程学院，北京 100044；2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044）

针对站间线路存在不同限速的情况，提出一种运行时间优化分配方法。根据影响速度曲线节能优化的限速划分了优化区间，建立每个优化区间的能耗—时间函数，借助拉格朗日法建立增广目标函数，通过拟牛顿法迭代得到站间运行时间优化分配结果，采用Matlab进行仿真。当区间的线路限速数量和限速值不同时，也可以通过该方法进行站间运行时间的优化分配。最后在基于CMC芯片的硬件环境下进行了测试。

列车控制；节能优化；时间分配；CMC芯片

相比于其他的交通模式，城市轨道交通具有运量大、占地少、安全准时、速度快等特点。轨道交通的能耗是指列车牵引、通风空调、电梯、照明、给排水、弱电等设备产生的能耗。据北京发展与改革委员会[1]北京市各线路车站能耗和车辆能耗统计，2009年北京地铁总用电量为5.55亿kW·h （不含轨道交通机场快轨专线），其中，牵引能耗 3.07亿kW·h，占总能耗的52.74 %。因此，研究轨道交通系统的节能问题对于降低运输成本、提高经济效益以及促进轨道交通的可持续发展都具有重要的现实意义。

列车节能操纵是一个搜索最优值的问题，在满足时刻表给定的运行时间条件下，寻找列车站间牵引能耗最小的速度—距离曲线，约束条件包括线路信息，车辆信息等。本文从站间运行时间分配的角度研究了列车速度—距离曲线节能优化问题，提出一种运行时间优化分配算法，并在国产芯片CMC环境下进行了算法测试。

1 时间分配优化模型及求解

考虑到安全问题，列车在通过某些区域时需要低于限速运行。定义直接影响速度-距离曲线形状的限速值为“优化有效限速值”，每个“优化有效限速值”对应一个限速带。站间线路被限速带划分成若干区间，如图1所示，两站之间形成了两个限速带和3个限速区间。该站间的列车速度曲线节能优化问题可以转化为几个独立区间的时间分配问题。

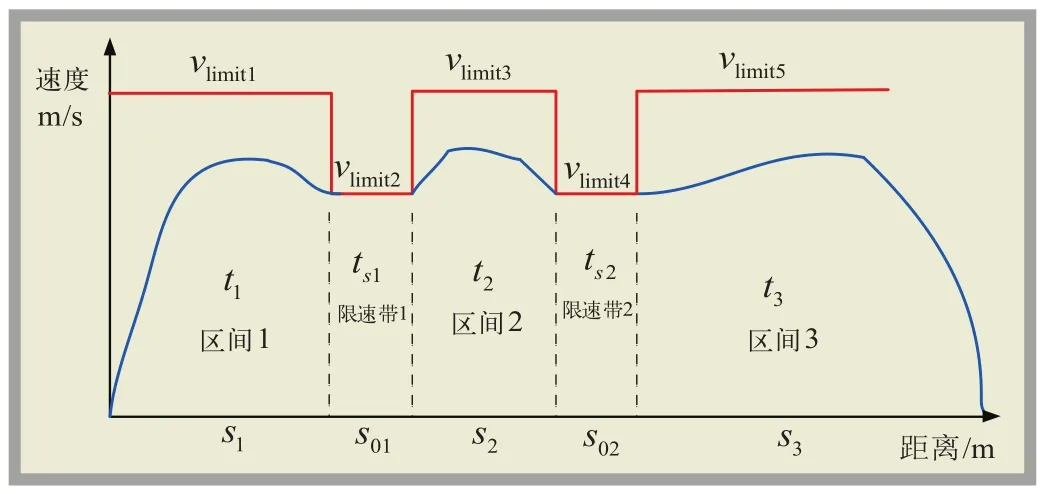
图1 站间不同限速下的列车速度曲线示意图

以图1的线路为例，假设站间距离为S和总运行时间为T，列车在两个限速带上按照规定的限速值匀速运行，那么列车在限速带1和限速带2的运行时间已知。该站间的节能问题转化为3个区间（区间1、区间2和区间3）的运行时间的分配问题，结合列车动力学微分方程，将该优化问题定义为：

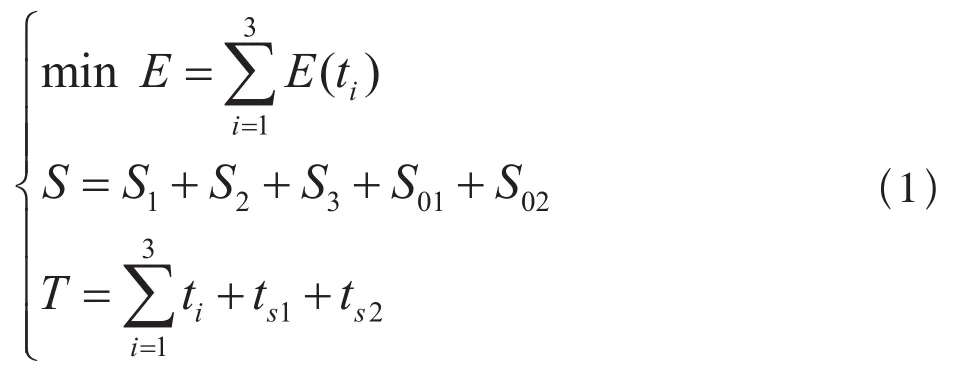
其中，ti和E(ti)分别表示各个区间的运行时间和能耗-时间函数。ts1、 ts2和E1、E2分别是两个限速带的运行时间和能耗，可根据假设条件直接计算。

对于上述条件的极值问题可以采用拉格朗日乘数法，借助拉格朗日乘数建立的增广目标函数为：

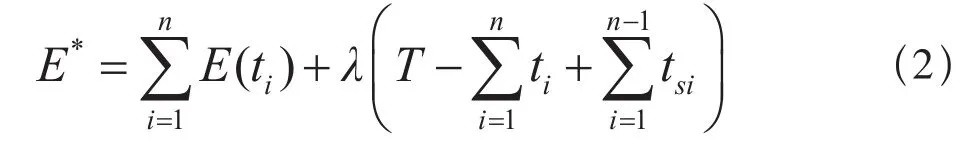
在优化问题中有3个区间，n=3，所以式中含有t1、t2、t3和λ几个变量。上述增广函数极值点有以下几个必要条件。

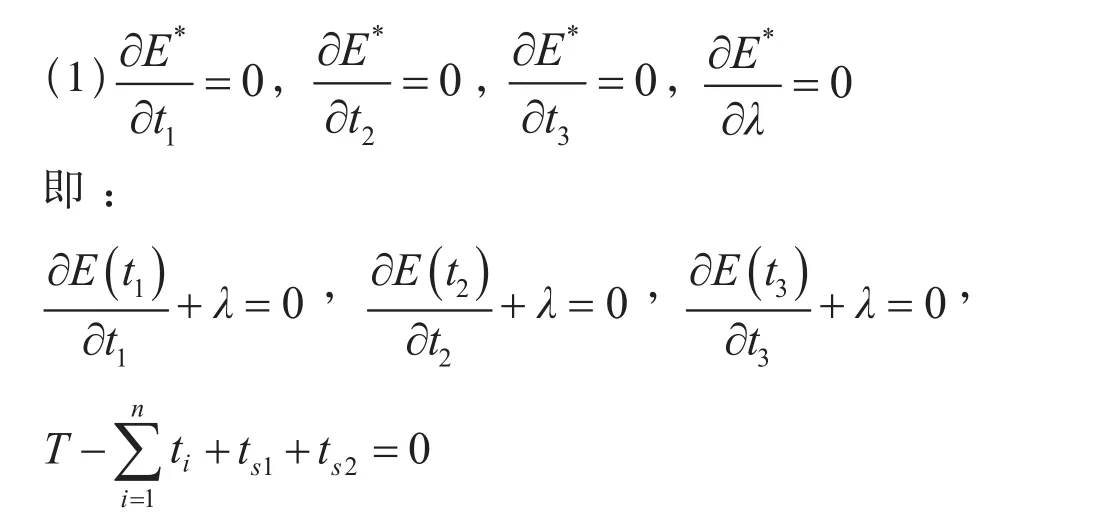
最后一个等式是等式约束条件，其余各式可以统一换成一个形式为：

（2）在约束条件下，拉格朗日乘数具有一定数值，但是在实际问题中有限制范围，除了考虑等式约束之外，还要考虑上下限的不等式约束。

可以运用Kuhn-Tucker方法：

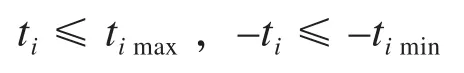
增广目标函数变为：

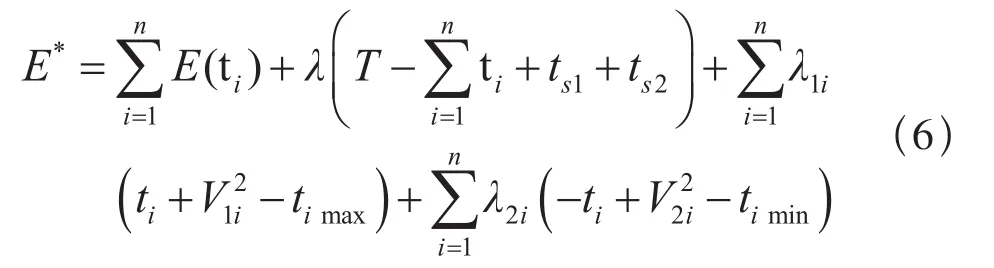
（3）极小值点的必要条件，即Kuhn-Tucker条件：

根据Kuhn-Tucker条件，λ1i及λ2i不能为负值，由得到：

最后，通过拟牛顿法进行迭代求解。

2 仿真实例

单质点模型将列车视为单质点，列车运动符合牛顿运动学定律。在限制速度的约束下列车通常包含4种运行工况：牵引、巡航、惰行和制动[2]。

牵引阶段：列车处于加速过程，发动机牵引耗能；巡航阶段：列车保持匀速运行，所受到的合力为零，列车需要牵引还是制动取决于列车当时所受到的阻力，若处于牵引阶段则耗能；惰行阶段：列车发动机既不牵引也不制动，运行状态取决于当时受到的阻力之和，通常在非下坡道上列车均处于减速状态；制动阶段：列车在该阶段减速至规定速度，发动机不耗能。若配备再生制动，发动机反转变为电动机产生再生电流，可利用多车协同的方法吸收部分再生能量[3]。列车及线路参数设定如表1所示。

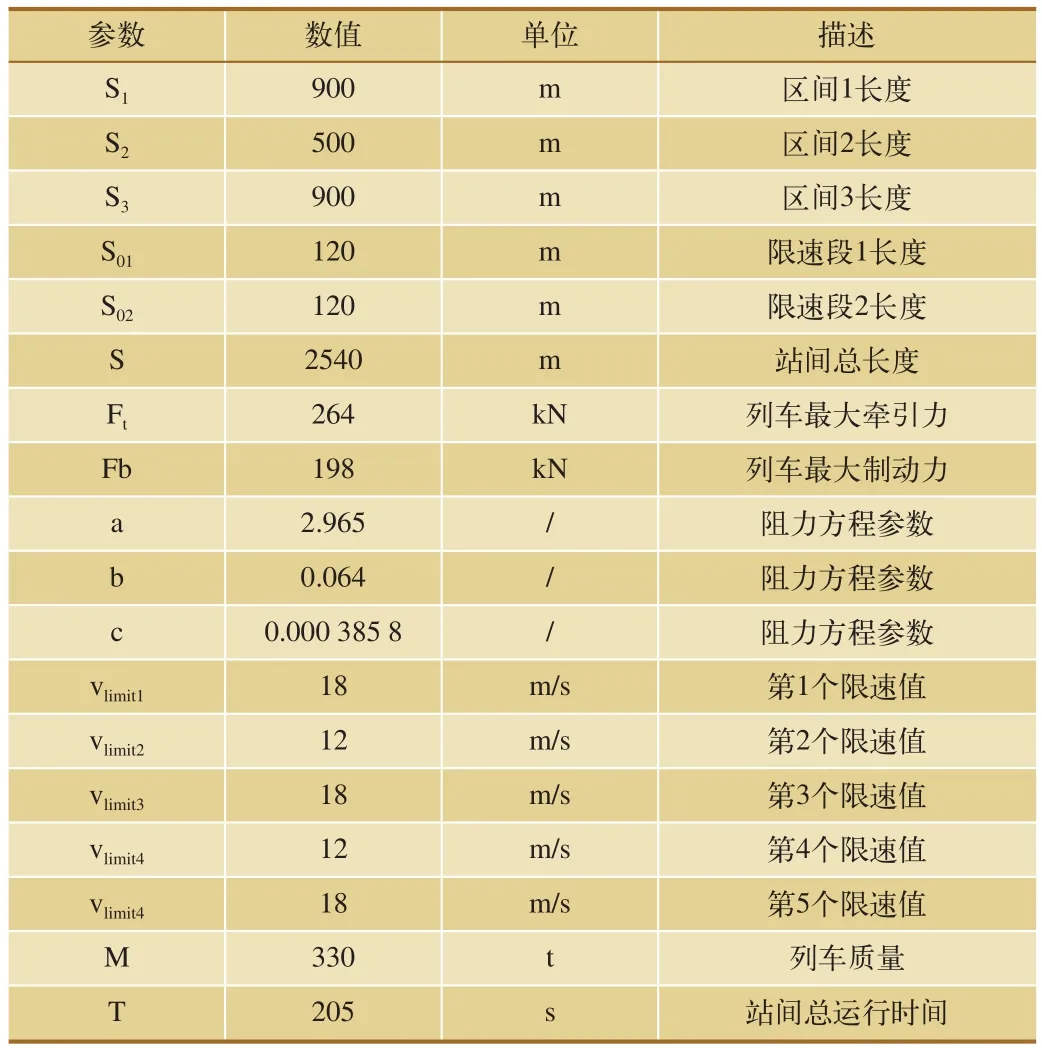
表1 列车及线路各参数值

对于区间1来说，给定运行时间t1，存在一条是能量消耗最低的速度曲线。结合列车动力学模型，当t1不同时，最优速度曲线也不相同。在这里需要强调的运行时间t1的取值具有一定的范围[4]，t1过小会导致列车无法在时间段内完成规定的运行距离，t1过大列车运行速度过低，不能满足运营要求。根据区间1的线路情况，结合列车动力学模型得到：

其中，g(x)为x处单位质量重力分量，正为上坡，负为下坡。从上述公式的目标函数和约束条件可以看出，限速区间1的优化问题是属于非线性优化问题，在Matlab工具中提供了求解有约束的非线性规划问题求解函数fmincon。用Matlab求解列车在不同 t1值下的能量最优曲线，结果如图2所示，从上到下依次为 t1时间段是65 s，70 s，75 s和80 s时的能量最优速度曲线。在不同时间下对应有不同能量消耗，具体数据如表2所示。

图2 区间1在不同运行时间下的速度曲线仿真

表2 区间1不同运行时间下对应的能耗

根据这些数据就可以用最小二乘法拟合能量消耗与时间的函数，利用二次函数就可以很好的满足需求[5]。经表2数据拟合得到的曲线如下：

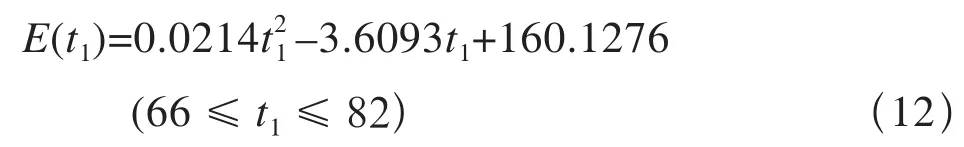
同理，可求出区间2和区间3的能耗时间方程分别为：

计算出限速带1的能耗：

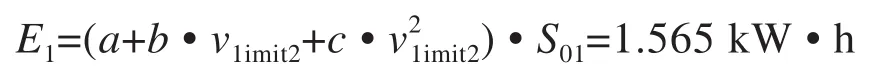
同理，限速带2的能耗为：E2=1.565 kW · h

在求得3个区间的能耗-时间方程后，可将公式（1）中的优化问题写作：

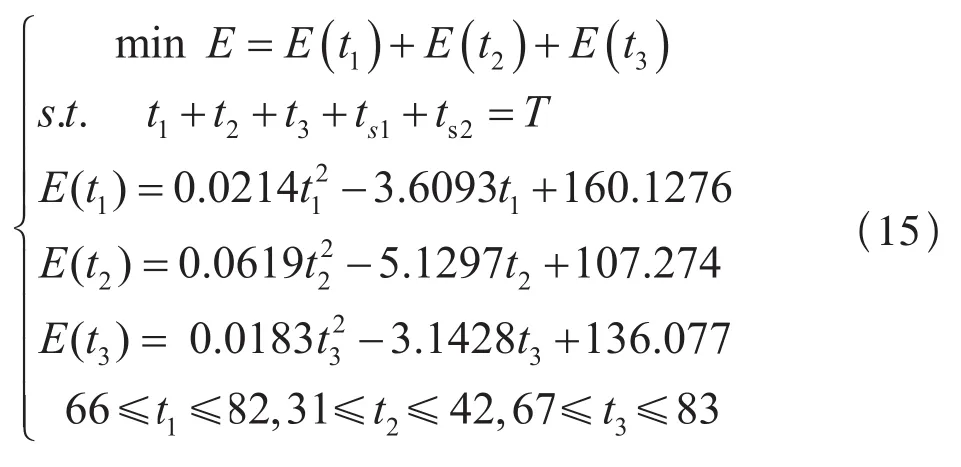
其中，T、E1、E2、ts1和ts2均为已知，根据上述原理，通过计算机迭代求得：

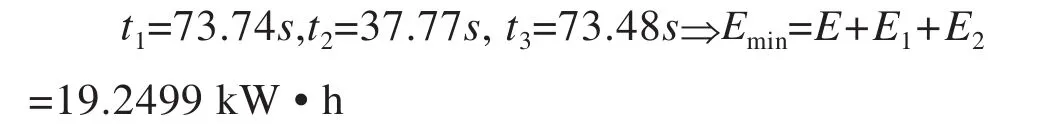
根据求得的区间1到区间3分配的时间，生成两站间的最优速度距离曲线如图3所示。

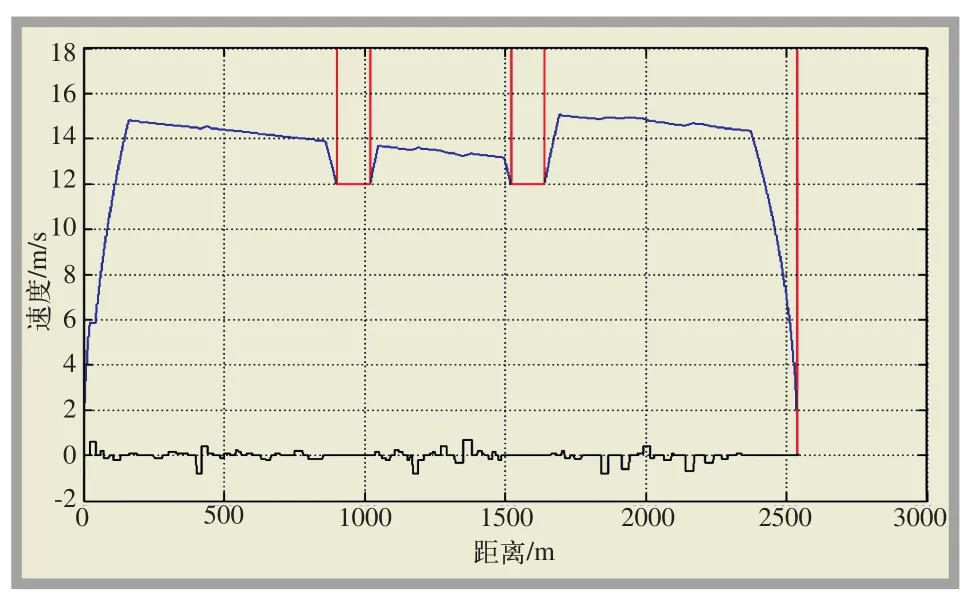
图3 最优时间分配下的速度曲线仿真图

3 硬件测试

为测试该算法搭建了基于CMC芯片的半实物仿真平台，并且在平台软件上得到了目标速度曲线，如图4所示。基于CMC芯片的半实物仿真平台的设计包括系统硬件部分：外围电路和驱动程序；系统软件部分：上位机PC端仿真软件。其中，硬件系统的作用是为列车节能控制算法提供硬件运行环境，并且与上位机软件系统进行实时通信、实现数据交互；软件系统的作用是实现列车模型的仿真和列车运行环境的仿真，并且和下位机硬件系统进行数据通信[6]。

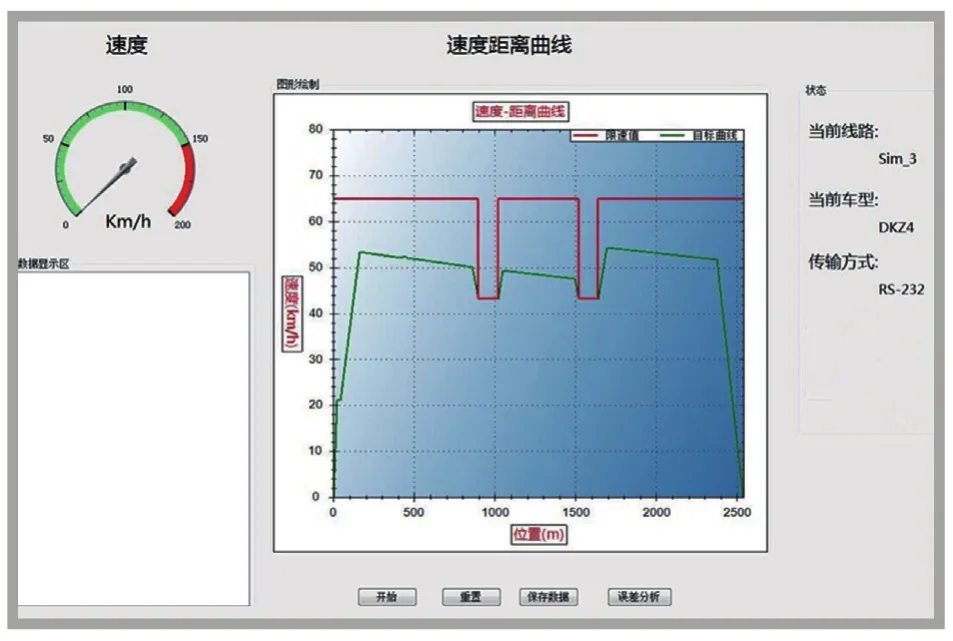
图4 时间分配算法在CMC平台测试后得到的最优速度距离曲线

4 结束语

本文通过列车站间运行时间优化分配，解决列车在不同限速场景下的节能优化问题。该方法同样适用于不同参数的限速场景，通过计算得到各区间的能耗-时间方程，便可以根据这种非线性规划方法得到站间运行时间分配结果，从而优化该站间的列车运行能耗，达到节能的目的。

[1]袁宏伟,孔令洋.城市轨道交通能耗影响因素及测算研究[J].都市快轨交通，2012，25（2）：41-44.

[2]Liu,R.R,Golovitcher,I.M.Energy-effcient operation of rail vehicles[J].Transportation Research Part A:Policy and Practice,2003,37(10):917-932.

[3]Sun X,Cai H,Hou X,et al.Regenerative braking energy utilization by multi train cooperation[C].Intelligent Transportation Systems (ITSC),2014 IEEE 17th International Conference onIEEE,2014:139-144.

[4]Sun X,Cai H,Hou X,et al.Energy consumption analysis with trip time for a single train[C].26th Chinese Process Control Conference,2015:1-5.

[5]孙德敏.工程最优化方法及应用[M].合肥：中国科技大学出版社，1991.

[6]侯晓伟，孙绪彬，蔡 虎，等.基于ARM的列车运行控制算法仿真测试系统[C].第26届中国过程控制会议，2015：20-25.

责任编辑 陈 蓉

Optimization of train speed profle based on inter-station running time distribution and its simulation test in CMC environment

CAI Hu1,HOU Xiaowei2,ZHANG Jiemin2,YANG Yang2
( 1.School of Electronic and Information Engineering,Beijing Jiaotong,University Beijing 100044,China;2.State Key Laboratory of Rail Traffc Control and Safety,Beijing Jiaotong University,Beijing 100044,China)

This article proposed an optimization method for inter-station running time distribution of a train,as the line speed between two stations was limited.The inter-station line could be divided into several intervals based on the number and the values of the speed limits which infuence the speed profle directly.The Energy-Time function of each interval could be calculated through function ftting.The article established an augmented objective function via Lagrange multiplier.The simulation was taken by Matlab,and the optimization results for inter-station running time distribution were obtained by the Quasi-Newton method.This method could be applied to lines with different speed limits if the Energy-Time function of every interval could be obtained.This method was tested based on the hardware environment of the CMC chip .

train control;energy saving optimization;running time distribution;CMC(Control Model on Chips) chip

U268.4∶TP39

A

1005-8451（2016）05-0006-04

2015-10-20

863计划项目（2012AA041701-3）。

蔡 虎，在读硕士研究生；侯晓伟，在读硕士研究生。