基于粒子群支持向量机的轨道电路故障诊断

陈 欣

（西南交通大学 信息科学与技术学院，成都 611756）

基于粒子群支持向量机的轨道电路故障诊断

陈 欣

（西南交通大学 信息科学与技术学院，成都 611756）

支持向量机（SVM）是一种解决小样本分类问题的最佳理论算法，它的核函数的参数选择非常重要，直接影响着故障诊断的准确率。本文将粒子群算法（PSO）用于支持向量机的参数优化，提出基于粒子群支持向量机的故障诊断模型，并将其运用于轨道电路中。通过对比MATLAB仿真结果得出：经过粒子群寻优得到的参数比随机选取的参数更优，所建立的PSO-SVM模型的故障诊断准确率高于普通的SVM模型。

轨道电路；故障诊断；支持向量机；粒子群算法

无绝缘轨道ZPW-2000A在我国铁路系统中占据着非常重要的作用，主要用于站间闭塞区间和站内电码化。作为铁路信号系统中最重要、最关键的基础设备之一，轨道电路的结构很复杂，故障也是多样化的，设备运用损耗、检修维护不到位和环境因素都可能对轨道电路造成影响。目前，针对ZPW-2000A型无绝缘轨道电路的故障诊断仍然停留在人工阶段，主要依靠故障区段的无绝缘衰耗盘指示灯对故障的定位和对测试塞孔进行的电气特性测试[1]，根据所测试的数据进行故障判断和分析，依赖的是维修人员对设备故障的处理经验和知识，存在很大的盲目性和复杂性。因此，轨道电路的故障检修工作亟待完善。

支持向量机（SVM）是一种以统计学习理论为基础的机器学习方法，相比较人工神经网络等方法的缺点，如网络结构难于确定、过学习、欠学习，以及局部极小等问题，SVM对于解决有限样本更优，被认为是目前解决有限样本分类问题的最佳理论[2]。本文将利用粒子群支持向量机理论建立更为有效的轨道电路故障诊断模型，实现多种故障的诊断。

1 ZPW-2000A轨道故障分析

1.1 ZPW-2000A轨道电路构成

ZPW-2000A型无绝缘轨道电路系统由室内部分和室外部分组成，室外部分包括调谐区、机械绝缘节、匹配变压器、补偿电容、传输电缆及调谐设备引接线，其中,调谐单元、空心线圈、钢轨中的电容、电阻、电感等元器件组成的电路实行串、并联谐振，实现了两个相邻轨道电路之间的电气绝缘；传输电缆采用的是SPT型的国产铁路数字电缆，传输控制信息及电能；匹配电压器是为了使轨道电路和SPT 电缆实现匹配连接；补偿电容则延长了传输的距离，实现电路的补偿，可以获得最佳的传输效果。室内部分包括发送器、接收器、衰耗盘、电缆模拟网络盘和站防雷，其中,发送器和接收器都具有较完整的监测功能，发送器产生稳定的移频信号，分别向主轨道电路和小轨道电路传送，再经过钢轨、匹配变压器、电缆通道，最后被主轨道电路的接收器接收，而流向小轨道电路的信号，则由运行前方的相邻的轨道电路接收器接收；衰耗盘的作用是对主轨道电路的接收端输入电平调整，以及对小轨道电路正反向的调整[3]。

1.2 ZPW-2000A轨道电路故障分析

ZPW-2000A轨道电路常见的故障有红光带和分路不良两种[4]，红光带是指轨道上本来没车占用，战场图中显示有车占用，严重的影响了运输效率；而分路不良则是指本来有车占用，战场图中却显示无车占用，可能引发严重的事故，两个方面都应该尽量减少和避免。轨道电路的故障有两种处理方式：有报警故障处理和无报警故障处理[5]，红光带故障属于无报警故障，需要通过一些判断分析，测定故障范围，区分是室内故障还是室外故障，再判断具体的室内或室外故障点。ZPW-2000A无绝缘轨道电路的常见故障点主要包括主轨道故障、小轨道故障、发送通道故障和接收通道故障。

2 PSO-SVM算法的实现

2.1 支持向量机的基本理论

支持向量机是由Vapnik提出的一种新型算法，主要思想是建立一个超平面用于模式分类，将正例和反例分隔开，并尽量最大化隔离边缘，SVM是结构风险最小化的近似实现。线性可分问题易于分类，对于线性不可分问题，SVM通过一个非线性映射φ，把样本空间映射到一个高维的特征空间，转化为高维空间中的线性问题，在变换空间中求出最优分类超平面[6]。决策输出函数表示为：

其中， a*—拉格朗日乘子；

偏置b*可通过a*求得； K(x,xi)—核函数。

SVM中常用的核函数有多项式函数k(xi,xj)=(xixj+b)d，径向基函数（RBF)，其中，核参数的选择问题非常重要，一个好的核参数构成的支持向量机不但具有很好的推广能力，还具有更好的分类能力，由于RBF中只需要确定一个参数σ，因此本文核函数选用RBF，较少的核参数需要确定，更有利于参数优化。

2.2 粒子群算法原理

粒子群算法（PSO）的主要思想是在可解空间中初始化一群粒子，每个粒子由位置、速度和适用度值确定，适用度值由适用度函数计算得到。粒子在解空间中运动，通过跟踪个体极值点和群体极值点来更新自己的位置，个体极值Pbest是指个体所经历位置中计算得到的适应度值最优位置，群体极值Gbest是指种群中所有粒子搜索到的适应度最优位置[7]。粒子不断地更新位置，每更新一次就重新计算一次适应度值，再通过比较适应度值，更新个体极值Pbest和群体极值Gbest。

在每一次迭代过程中，粒子通过个体极值和全局极值更新自身的速度和位置，更新公式为：

式中，ω—惯性权重；

d=1,2,…,D；i=1,2,…,n；

t—当前迭代次数；

vid—粒子的速度；

c1和c2—非负常数，称为加速度因子；

r1和r2—分部于[0,1]之间的随机数。

2.3 PSO-SVM算法实现步骤

以RBF为核函数的支持向量机中有2个参数：惩罚参数c和核函数参数g，其中，惩罚参数c用于控制超出误差的样本惩罚程度，核函数参数g表示径向基函数RBF的宽度，c、g对于SVM的分类准确率有着很大的影响。因而，将两个参数（c，g）构成一个微粒，采用粒子群优化算法寻求较优的参数，提高SVM算法故障诊断的准确率和效率，该算法流程图如图1所示。

粒子和速度初始化是对由支持向量机中的两个参数构成的粒子（c，g）赋予随机的初始粒子位置和粒子速度，根据初始粒子适应度值确定个体极值和群体极值，再根据式（2）和式（3）更新粒子速度和位置，根据新种群中粒子适应度值更新个体极值和群体极值。对于本文中的适应度值也即轨道电路故障诊断的准确率。

图1 PSO-SVM算法流程图

3 基于PSO-SVM的轨道电路故障诊断模型

3.1 特征提取

为了建立粒子群支持向量故障诊断模型，本文选取正常状态、主轨道故障、小轨道故障、发送通道故障、接收通道故障5种状态作为模型的输出，根据上述故障发生后各特征参数的变化，选择主轨道输出电压、小轨道输出电压、轨入电压、衰耗器测试空电压、模拟盘电压作为故障诊断特征量作为输入。

因为各轨道电路故障诊断特征值具有不同的数量级，为了避免对PSO-SVM模型进行训练的过程中出现病态矩阵，同时也方便数据处理，使程序加快收敛，因此需要对训练样本和测试样本进行归一化预处理，采用的归一化映射公式如下：

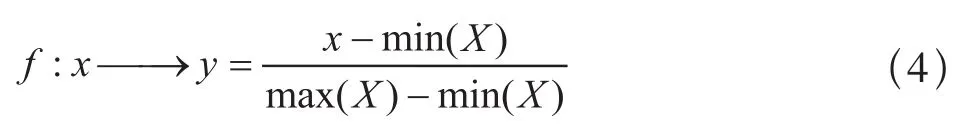
其中，y—归一化后的数据；

x—原始数据；

min(X)—原始数据中的最小值；

man(X)—原始数据中的最大值。

这种归一化的方式称为[0,1]区间归一化，处理后的数据位于[0,1]区间。

3.2 模型的构建

基本的SVM算法是针对二类别分类问题提出来的，是一种二类分类器，故障诊断属于多分类问题，轨道电路的故障诊断选取了5种状态，也即5种类别，SVM的多分类法有“一对一”、“一对多”等方法[8]。对于一个k类分类问题，“一对一”方法需要构造k(k–1)/2个SVM子分类器，训练速度快，每一个分类问题的规模较小；“一对多”方法需要构造k个SVM子分类器，分类速度相对较快，但是训练时间过长，因此本文采用“一对一”SVM多分类法构成轨道电路故障诊断模型。“一对一”方法的主要思想是在 类分类中，对每两类样本分别建立一个支持向量二类分类器，需要建立k(k–1)/2个二分类器，因此对于轨道电路故障诊断的5类分类问题，则需要构造10个二类分类器，测试时采用的是投票法，将测试样本x分别带入上述建立的10个二分类器进行测试，如果x属于第i类，则在第i类投票上加1，否则在第j类投票上加1，直到10个支持向量二分类器完成分类，累计5种类别的得票结果，得票最多的类则为测试样本所属的类别。

3.3 诊断结果分析

为了验证算法的正确性，采集 170组轨道电路的相关数据，从中选取100组作为训练样本，另外70个作为测试样本，进行故障诊断。为了验证所建立的PSO-SVM模型更优，通过2种方法选取惩罚参数c和核函数参数g：（1）在一定的范围内随机选取15组参数c、g，得到的最高诊断准确率为88.57%，此时，c=5，g=8，诊断时间约为3 s；（2）采用PSO

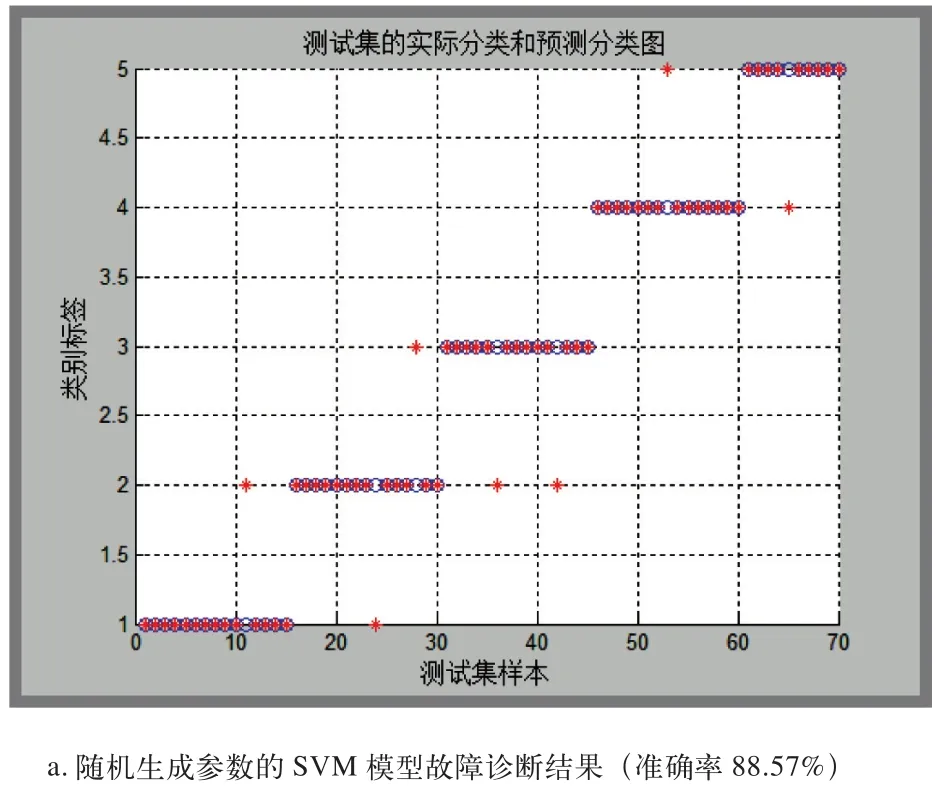
快速寻优得到最优的参数c、g，设定粒子个数为m=20，学习因子c1=1.5，c2=1.7，最大迭代数t=200，最终得到的最优参数c=12.29，g=3.76，故障诊断准确率为97.14%，诊断时间约为29.46 s，结果如图2所示。

Track circuit fault diagnosis based on particle swarm optimization and support vector machine

CHEN Xin
( School of Information Science and Technology,Southwest Jiaotong University,Chengdu 611756,China)

Support vector machine (SVM) is one of the best theoretical algorithm to solve the problem of small sample classifcation.Kernel parameter selection is very important,which directly affects the accuracy of fault diagnosis.In this paper,the particle swarm optimization (PSO) was used to optimize the parameters of SVM,the PSO-SVM model was proposed which was applied to fault diagnosis of track circuit.By comparing the MATLAB simulation results,it was concluded that the parameters obtained by PSO were better than the random parameters,and the fault diagnosis accuracy of the established PSO-SVM model was higher than that of the ordinary SVM model.

track circuit;fault diagnosis ;support vector machine(SVM);particle swarm optimization(PSO)

U284.2：TP39

A

1005-8451（2016）08-0056-04

2016-01-22

陈 欣，在读硕士研究生。