7～14岁儿童随机性认知的发展*

巩子坤何声清

（1．杭州师范大学理学院，杭州311121；2．北京师范大学教育学部，北京100875）

7～14岁儿童随机性认知的发展*

巩子坤1**何声清2

（1．杭州师范大学理学院，杭州311121；2．北京师范大学教育学部，北京100875）

采用三个典型的随机性认知任务（点分布认知，一维分布认知，二维分布认知）系统考察了7～14岁儿童随机性认知的发展特点。结果发现，随机性认知的发展随年龄增长而动态变化，7～10岁表现出上升趋势，而11～14岁表现出下降趋势。点分布认知的发展在7～11岁为缓慢上升，至12～14岁保持稳定。一维分布认知的发展在7～10岁为缓慢上升，在11岁开始迅速下降，至13～14岁趋于稳定。二维分布认知的发展在7～14岁始终处于较低水平。10～11岁是随机性认知发展的重要时期。

发展 随机性认知 点分布认知 一维分布认知 二维分布认知

1 引 言

概率概念认知是概率统计的基础与核心环节。对随机性的认知是概率概念认知的一个重要方面。随机性中隐藏着规律性，对随机性的认知本质上就是对规律性的认知。

在日常生活中，随机事件随处可见（Gal，2005），所以非正式概率知识的获得有着坚实的现实基础（Sharma，2012）。儿童在发展早期（甚至学前阶段）已经具备初步的随机思维和良好的概率直觉（Yost，Siegel＆Andrews，1962；Goldberg，1966）。Kuzmak和Gelman（1986）的研究发现儿童在小学阶段已经表现出对随机性的敏感性，比如，学前儿童能辨识“最有可能发生的结果”（Pange，2003），他们能够理解某些简单事件的可能性（Falk＆W ilkening，1998；Jones et al．，1997）。然而，近期研究发现，学龄儿童对随机性的理解仍然存在困难。在典型的研究随机性认知的“摸球”或“掷骰子”范式中，学龄儿童对随机结果的认知出现了不同程度偏离。Truran（1994）发现，儿童常常认为随机结果是由不可控因素（比如上帝、神灵等）决定的，而这一错误认识直至中学阶段依然存在，如Amir和W illiams（1999）对38名11～12岁儿童的研究发现，一些儿童在对随机事件结果作出判断时依然认为是“上帝控制了世界上发生的一切”。儿童也会把随机结果归结为球或骰子本身的特征（如构造和外形等）（Sharma，2012；Watson＆Moritz，2003）。儿童对随机性的理解未随年龄增长而增长，他们处理随机性的能力反而在退化（Engel＆Sedlmeier，2005）。Engel等（2005）在一项研究中采用抛硬币、雪花分布等认知任务（详见测查材料），通过问卷调查考察了11～15岁儿童随机性认知的发展特点。结果发现，儿童对随机性的认知并没有随着年龄的增长而增长，在抛硬币任务中不同年龄儿童的成绩没有显著差异；在雪花分布任务中，随着年龄增长，儿童的随机性认知水平却表现出倒退趋势。

更重要的是，随机性认知有不同的复杂程度，包括点、线、面三个层次：点分布认知，即随机事件；一维分布认知，即一维独立随机序列；二维分布认知（详见测查材料）。但是，目前对随机性认知的发展研究主要关注的是点分布认知（Lecoutre，1992；Sharma，1997），较少有研究直接探讨儿童对一维分布及二维分布的认知（Konold，Pollatsek，Well，Lohmeier＆Lipson，1993）。而且，以往研究多以某一阶段的儿童（如11～15岁，Green，1982；Engel＆Sedlmeier，2005）为研究对象，较少对从低到高不同阶段的儿童进行探讨。因此，现有研究都难以完整揭示随机性认知是如何萌芽及发展的。

因此，本研究选取7～14岁儿童为研究对象，采用问卷调查（Engel，2005；Green，1982），考察不同复杂程度的随机性认知（点分布认知、一维分布认知和二维分布认知）发展特点及进程。

2 研究设计

2．1 被试

为保证样本的代表性，研究采用分层随机取样方式，选取浙江省杭州市城区、城乡结合地区及农村地区三种类型学校的771名7～14岁儿童作为研究对象。其中，7岁儿童88名（平均年龄为7．4岁，男孩48名），8岁儿童86名（平均年龄为8．4岁，男孩41名），9岁儿童98名（平均年龄为9．4岁，男孩49名），10岁儿童103名（平均年龄为10．4岁，男孩50名），11岁儿童101名（平均年龄为11．4岁，男孩60名），12岁儿童96名（平均年龄为12．5岁，男孩49名），13岁儿童98名（平均年龄为13．5岁，男孩55名），14岁儿童101名（平均年龄为14．4岁，男孩49名）。

2．2 研究程序

2．2．1 测查材料

如前所述，随机性认知包括三个层次：点分布认知、一维分布认知和二维分布认知。为此，本研究采用三类认知任务，分别考察三个层次的随机性认知。具体如下：

点分布认知任务。一个不透明的盒子里有1个白球、1个黑球和1个绿球，它们除颜色外都相同。闭上眼睛，摇一摇盒子后，从盒子里摸出2个球。请问：摸出的这两个球一定是一个白球、一个黑球吗？

（ ）

A．一定 B．可能 C．不可能

一维分布认知任务。一个均匀的圆形卡片，一面写着1，一面写着0。抛这个卡片，1朝上就写1，0朝上就写0，一共抛10次。请在下面的表格中依次写出这10次朝上的结果，并写一写你的理由。

二维分布认知任务。花园房顶是平的，由16块尺寸相等的方砖构成。开始下雪了，过了一会，16片雪花飘落到房顶。请标出16片雪花可能落在什么地方（用×表示一片雪花），并写一写你的理由。

2．2．2 数据收集

为了保证儿童理解任务的内容，对低年龄儿童（9岁以下），我们通过实物演示任务的具体要求，以帮助他们理解题意。对于10岁及以上儿童，不再演示任务的具体要求。所有儿童以班级为单位，参加集体测试。测试时间30分钟。

2．2．3 计分

主试对儿童完成每个任务的反应评分，正确记1分，错误记0分。三个认知任务，总分为3分。具体评分标准如下：

点分布认知。如果儿童能够认识到这是一个随机事件，即选择“B．可能”，则记为1分，否则记为0分。

一维分布认知。如果儿童给出了随机的序列，则记为1分，否则记为0分。什么是随机的序列呢？我们采用游程检验的方法来进行统计推断。把儿童回答的原始数据录入数据库，以0．5为割点，进行游程检验。比如儿童回答的原始数据是：1010010111，游程检验的结果是：Case＝10，Runs＝7，Z＝0．49，p＝0．632。从而该序列具有随机性。再比如，对于原始数据1010101010，游程检验的结果是Case＝10，Runs＝10，Z＝2．35，p＜0．05，从而该序列不具有随机性。原始数据1111111111是一种极端情形，无法进行游程检验，但是，显然，这个序列是不随机的。

二维分布认知。如果儿童所描述的方砖上的雪花总数恰好为16片，且雪花所占的方砖数在7～13之间，且雪花分布没有明显的规律性，我们判定这样的雪花分布是随机的，记为1分，否则为0分。

有关研究根据儿童的回答情况，把回答分成4类（Engel＆Sedlmeier，2005）：严格的决定论，明显的可以识别的模式，每块方砖有一片雪花，雪花落在了正中，没有方砖是空缺的。适度的决定论者：可以看到明显的模式，每块方砖上有雪花，雪花在方砖上的位置比较随意。新手：不能够觉察到明显的模式，至少一块方砖是空的，但是，每块方砖上雪花的数目变化不大。专家：似乎是随机分布，没有明显的模式。有4～8块方砖是空的，没有对称性与规律性，雪花随机地落在方砖上。这是一种近乎定性的分析，并没有给出定量的刻画。特别地，对于儿童给出的原始数据，没有给出随机与否的结论。我们首先从概率原理上，彻底解决了这个问题。

16片雪花随机落入16个方砖中，M为空的方砖数，N＝16－M为有雪花的方砖数。那么，

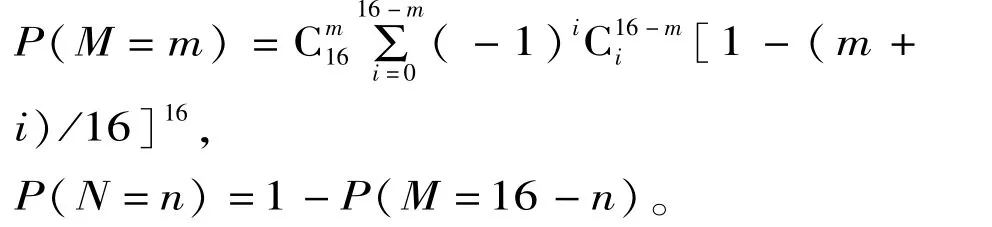
根据上面的公式，我们可以得到的概率分布，基于该分布，可以得到置信度的接受域［7，13］。例，假如有雪花的方砖数N＝8，方砖数在接受域中，那么认为雪花的分布是随机的。假如有雪花的方砖数N＝4，方砖数不在接受域中，那么认为雪花的分布不是随机的。

再进一步：若儿童给出的回答在接受域［7，13］之内，再观察儿童给出的答案是否具有明显的规律性（如严格关于中轴线对称等），若有明显规律可寻，则判定为不具有随机性。比如，以下的回答就不具有随机性。

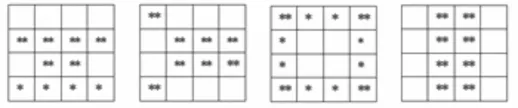
如果雪花数目超过或者不足16片，均作无效数据处理。

3 结 果

3．1 问卷的信度

以Cronbachα系数为指标，考察了每个认知任务的得分及测验总分的内部一致性系数，结果显示，点分布认知α＝0．68，一维分布认知α＝0．87，二维分布认知α＝0．73，整个测验α＝0．69，表明该测验具有较高的同质性信度。

3．2 随机性认知的整体发展

表1呈现了7～14岁儿童三个随机性认知任务得分总和（即总分）的描述统计结果。从表中可以看出，儿童随机性认知的发展呈现出先上升后下降的趋势：7～10岁是上升阶段，10～14岁是下降阶段。在上升阶段，7～8岁和9～10岁表现出快速发展的趋势。在下降阶段，13～14岁表现出缓慢发展的趋势。

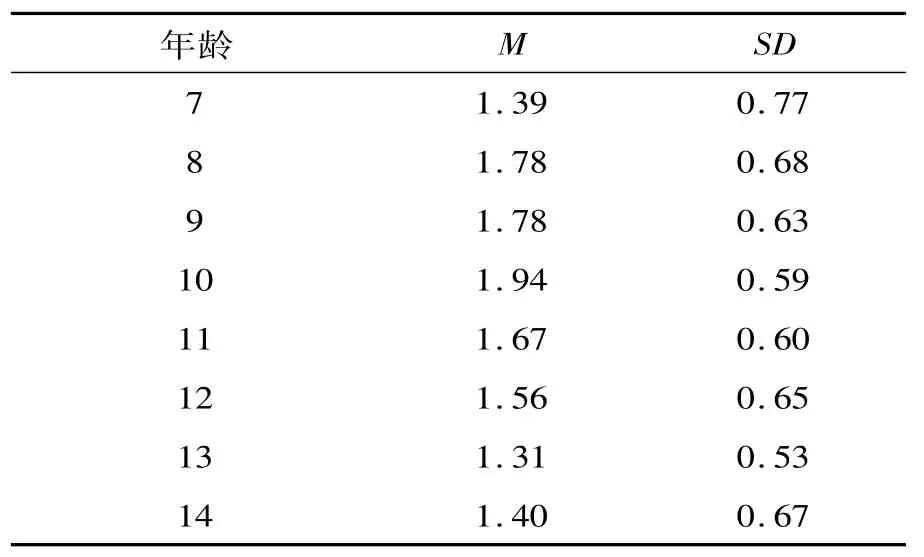
表1 7～14岁儿童的随机性认知得分描述统计

为了进一步检验上述发展趋势，我们以年龄为自变量，以总分为因变量，进行单因素方差分析。由于不同自变量分组的方差不齐，Levene（7，763）＝6．42，p＜0．001，选择使用方差分析（下同）。结果发现，年龄的主效应显著，Welch（7，324．30）＝13．71，p＜0．001，ηG2＝0．10）。这一结果提示，不同年龄儿童的随机性认知总分有着显著的差异。多重比较结果表明，7岁儿童的得分显著小于8～10岁的儿童（7岁vs．8岁，p＜0．05；7岁vs．9岁，p＜0．05；7岁vs．10岁，p＜0．01），但是大于13岁儿童（p＜0．05）。10岁儿童的得分显著大于11～14岁儿童的得分（10岁vs．11岁，p＜0．05；10岁vs．12岁，p＜0．01；10岁vs．13岁，p＜0．001；10岁vs．14岁，p＜0．001）。此外，11岁儿童得分显著大于13、14岁儿童（11岁vs．13岁，p＜0．001；11岁vs．14岁p＜0．05）。其他各组间的差异不显著（全部p＞0．05）。

3．3 三个层次随机性认知的发展

为更清楚揭示儿童随机性认知的发展特点，我们进一步比较了儿童三个层次（点分布、一维分布和二维分布）随机性认知的发展特点。

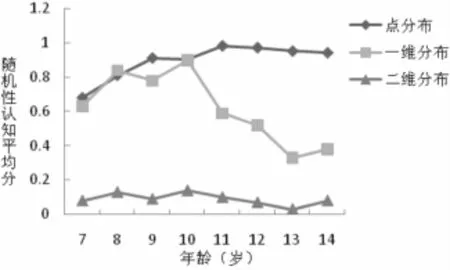
图1 7～14岁儿童三个层次随机性认知比较

图1呈现了各个年龄儿童三个层次随机性认知任务得分的发展曲线。以年龄（组间变量）和任务类型（组内变量）为自变量，对数据进行二因素方差分析。结果发现，年龄的主效应显著（F（7，763）＝12．39，p＜0．001，ηG2＝0．10），任务类型的主效应显著（F（2，1526）＝1114．16，p＜0．001，ηG2＝0．59）。年龄与任务类型的交互作用显著（F（2，1526）＝15．82，p＜0．001，ηG2＝0．13）。

简单效应分析结果显示，在点分布任务中，7岁儿童的得分显著低于9～14岁儿童（全部p＜0．01），8岁儿童的得分显著低于11～12岁儿童（全部p＜0．01），而9～14岁儿童之间没有显著差异（全部p＞0．05）。这一结果表明，从7岁到9岁，点分布认知快速发展，至9岁达到较高水平且保持稳定至14岁。

在一维分布认知任务中，7岁儿童的得分显著低于8岁、10岁儿童（全部p＜0．01），然而却显著高于13岁、14岁儿童（全部p＜0．01）；8～11岁儿童的得分显著高于13～14岁儿童（全部p＜0．01）；12～14岁儿童之间不存在显著性差异（全部p＞0．05）。这一结果表明，一维分布认知在7～10岁随年龄增长而上升，至10岁达到较高水平，随后却表现出下降趋势，11～12岁与7岁的水平相当，而13～14岁显著低于7岁的水平。10岁是儿童一维分布认知发展的转折点。

在二维分布认知任务中，不同年龄儿童之间的差异不显著（p＞0．05），这一结果提示，7～14岁儿童的二维分布认知都处于较低水平，尚处于萌芽阶段。

此外，各个年龄儿童对三个层次随机性认知的分化模式也有所不同。对7～10岁儿童，点分布认知的得分最高，其次是一维分布认知，最低的是二维分布认知。简单效应分析的结果表明，点分布认知和一维分布认知的得分没有显著性差异（全部p＞0．05），而点分布认知和一维分布认知的得分都大于二维分布认知（p＜0．05）。对11～14岁儿童，三个层次随机性认知得分的高低顺序虽然没有发生变化，但是三个层次随机性认知得分两两之间均有显著性差异，即点分布认知的得分显著高于一维分布认知和二维分布认知，而一维分布认知的得分显著高于二维分布认知（全部p＜0．05）。

4 讨 论

4．1 随机性认知发展的整体特点

从整体上看，儿童随机性认知的发展是一个动态变化的过程，7～10岁表现出随年龄增长的上升趋势（特别是7～8岁有明显提高），10岁达到较高水平；然后随年龄增长反而表现出下降趋势，11～14岁降到7岁水平（11岁和13岁是两个快速下降点）。进一步分析发现，点分布认知水平普遍很高（通过率90％），而二维分布认知普遍很低（通过率9％）。因此，一维分布认知对随机性认知的整体发展的动态变化有重要贡献。

4．2 三个层次随机性认知发展的特点

我们发现三个层次随机性认知的发展表现出不同的趋势。

点分布认知发展在7～11岁表现出缓慢上升，然后从12～14岁处于较稳定的水平。而且，7岁儿童的点分布认知的通过率已经达到较高水平（68％），11岁时达到了高峰（98％）。参考以往研究结果，分别以20％、50％及80％的得分率作为萌芽、理解及掌握的标准（沈家鲜，刘范，1984），8～14的儿童都能够掌握“点分布认知”。点分布认知就是我们日常生活中的随机事件，儿童容易获得。

一维分布认知发展也是动态变化的。7～10岁表现出随年龄增长的上升发展趋势，7～8岁是一个快速发展时期。10岁时达到了高峰且出现转折，11～14岁表现出随年龄增长而下降的发展趋势，10到11岁是快速倒退时期。Engel等（2005）曾经研究了11～15岁儿童一维分布认知的发展，结果显示，这些儿童之间没有显著性差异。而我们的研究表明，11～14岁儿童一维分布认知发展是显著下降的，不仅如此，我们还贯通研究了7～14岁儿童一维分布认知的发展，探查了“先上升、后下降”的趋势。进一步，10岁儿童的得分率是79％，已经基本掌握了“一维分布认知”，但是13～14岁儿童的得分率仅为45％，已经降低为理解水平。10～11岁的转折可能受教学因素影响。在9岁（三年级上学期），儿童初步学习了点分布认知（卢江，杨刚，2011a）。而本研究是在下学期进行的，所以对于10岁的儿童而言，已经有一年半没有接触相关知识了，他们的概率知识还比较薄弱，他们的概率知识主要局限于“圆形卡片正反面的可能性大概是1／2，所以正反面出现大概是5次”。但是，对于正反面各5次具体如何相继出现，他们还不知道其中的规律，只好遵循内心的随机性直觉，写出相应的结果，而这样的结果往往是随机的。近期一项对概率认知的发展研究表明，11岁儿童比10岁儿童的概率认知水平要高（巩子坤，2012）。对教材的分析发现，与10岁儿童相比，11岁儿童学习了更多的概率知识，因为在11岁（五年级上）的时候，他们又学习了用分数表示可能性的大小、理解何谓游戏公平等（卢江，杨刚，2011b）。相对10岁儿童，11岁儿童对“抛圆形卡片10次”的认知并非局限在“正反面出现的可能性均是1／2”这样的范围，而是认为应该有着更好的规律，这个规律导致的结果是——出现了1010101010这样的“有规律”的情形。当然，这样的规律也并不是老师有意识地教给他们的，因为，教材中没有这样的知识，考试不考这样的知识，课外培训机构也不教这样的知识——这些知识来自儿童寻求规律的潜意识，这样的潜意识正是确定性数学教学所追求的。比如，我们发现，相对于11岁儿童，更多的10岁儿童意识到，抛10次卡片，正反面出现的次数不一定正好各是5次。对儿童回答“正反面出现的次数相等与否”问题的分析发现，11岁儿童与10岁儿童有着明显不同：44．3％的10岁儿童认为正反面出现的次数不相等，而仅仅有22％的11岁儿童认为正反面出现的次数不相等。正反面出现的次数不等的结果往往是随机的结果。近一半的10岁儿童给出了正反面不等的结果，这表明“既然正反面出现的概率都是1／2，所以正反面各出现5次”这一规律还没有束缚住10岁的儿童，所以10岁儿童给出了随机的答案；而这一规律却牢牢地束缚住了11岁的儿童，进而给出了1010101010等不随机的答案。事实上，在抛10次的所有情形中，正反面各出现5次的可能性仅仅有1／4左右，也就是说，从理论上而言，应该有3／4的结果中出现正反面不是各5次的情形），但是却有超过3／4的11岁儿童选择了这个结果。

二维分布认知的发展在7～14岁始终处在萌芽水平，即便是相对较高的8岁和10岁，得分率也只有13％左右。这一结果与Green（1982，1986）、Engel等（2005）的研究结果并不一致：他们的研究表明，儿童（11～16岁，11～15岁）的认知水平随着年龄的增长在不断退化。导致儿童二维分布认知发展水平很低的主要原因是儿童遵循了“均匀分布”与“集中”的规律。所谓“均匀分布”是指，在儿童看来，既然每一片雪花落到每一块方砖的可能性是一样的，而恰恰是16块方砖、16片雪花，为了保持游戏的公平性，因而，每块方砖上应该有1片雪花（当然，日常生活经验也告诉我们，雪下了一段时间后，地面是平的）。所谓“集中”是指，在儿童看来，由于受到刮风等因素的影响，所有的雪花都集中在几块方砖上，而往往地，这些方砖的数目是4～6之间。这些“规律”不是概率的规律，基于这些“规律”所得到的结果都是不随机的（巩子坤，2012）。也许，只有儿童掌握了概率的理论知识后，才能够真正认识到二维分布的规律。

综上所述，三个层次随机性认知发展之间有较大差异。点分布认知就是我们日常的随机事件，容易获得，儿童的认知水平较高。儿童的生活经验与拥有的确定性数学知识对于认知一维分布而言，是一把双刃剑，既有利于获得该认知，又阻碍了该认知；特别的，随着年龄的增加，他们良好的随机性直觉在减弱，从而就比较难以获得该认知了。要认知二维分布，需要拥有较好的概率知识，而此时，儿童还不具备这些知识，所以，认知水平就很低了。

防震缝的宽度既不能太大，也不能太小。如果防震缝的宽度太小，在强烈地震下相邻结构就会发生局部碰撞而损坏；如果防震缝宽度过大，就会给建筑物的立面处理带来困难。因此，建筑抗震设计规范中对抗震缝的最小设计宽度给予了相关规定。防震缝可以结合沉降缝贯通到地基，无沉降问题时也可从地下室顶到屋顶贯通，无需贯通至地基。

4．3 对教学的启示

儿童一维分布认知水平在10岁出现倒退，值得我们反思：究竟是什么因素影响了儿童良好的随机性直觉？在教学中，如何呵护儿童的良好直觉？这值得深入思考。同时，我们也需要对这样的教学困难有着充分的思想准备。我们曾经听了一节小学六年级的复习课，内容是：“鸡妈妈孵出了10只鸡宝宝。请问，这10只鸡宝宝，是5只小公鸡5只小母鸡的可能性大，还是4只小公鸡6只小母鸡的可能性大？”老师引导学习这样思考：这10只小鸡共有以下11种可能：0只小公鸡10只小母鸡，1只小公鸡9只小母鸡，……，10只小公鸡0只小母鸡。所以，上述可能性一样大。得到这样的结论后，全班一致赞同，没有反对的声音。该问题本质上就是“一维分布认知”。师生对该问题的错误认知表明，该问题是一个困难的问题。当然，正如上述调查所表明的，凡是基于试验得到的结论均是正确的，因而，我们可以引导儿童试验，通过试验来获得随机的结果，通过这些随机的结果，再总结、归纳出规律。这就真正地实现了“通过随机性来认识规律性”的目的。所以，不要过早地教给儿童形式化的结果，尤其是使用公式进行计算；而是要通过试验，通过动手，充分感受随机性，进而总结规律性——这也许是概率学习的有效方式与途径（巩子坤，宋乃庆，2006）。国外教科书“概率建模”的教学内容与学习方式，值得我们学习与借鉴。比如，对于鸡妈妈孵出10只鸡宝宝的问题，如果真正做试验，是很困难的：哪里找这样的鸡妈妈？怎样正好孵出了10只鸡宝宝？但是通过“概率建模”来解决就容易了：硬币的正面代表小公鸡，反面代表小母鸡，抛一次硬币，就孵出了一只鸡宝宝，抛10次，就孵出了10只鸡宝宝。

儿童二维分布认知的发展水平很低，在7～14岁之间始终在萌芽水平，这告诉我们，即便到了初中阶段，这部分内容都不适合进入课程内容。当然，我们也可以这样设想：可否通过试验、活动的方式开展这部分内容的教学。

4．4 不足与展望

本文所使用的测查材料是三个层次随机性认知任务，每一个层次的认知任务仅有一个，一定程度上影响了问卷的内部一致性系数。另外，从更加严格的角度思考，对于随机性的认知，是否仅仅有这三个层次呢？还有没有其他层次？这都是未来研究需要解决的重要问题。

5 结 论

（1）儿童随机性认知整体发展是一个动态变化的过程：7～10岁上升，11～14岁下降，10岁是发展的转折点。

（2）点分布认知发展可以分为两个阶段：7～11岁为缓慢上升发展时期，12～14岁为停滞发展时期。一维分布认知发展可以分为两个阶段：7～10岁为上升发展时期，11～14岁为倒退发展时期。二维分布认知发展整体处在同一个阶段与很低水平。

（3）7～10岁儿童，点分布认知、一维分布认知有着相近的得分与发展趋势，并且显著高于二维分布认知。11～14岁儿童，点分布认知得分显著高于一维分布认知、二维分布认知，一维分布认知显著高于二维分布认知。

巩子坤．（2012）．6～14岁儿童的概率概念认知发展研究．杭州：浙江大学，6－56．

卢江，杨刚．（2011a）．数学（三年级（上））．北京：人民教育出版社，104－111．

卢江，杨刚．（2011b）．数学（五年级（上））．北京：人民教育出版社，98－108．

沈家鲜，刘范．（1984）．5－17岁儿童和青少年容积概念发展的研究．心理学报，1984（2）：155－164．

Am ir，G．，＆W illiams，J．（1999）．Cultural Influences on Children's Probabilistic Thinking．Journal of Mathematical Behavior，18（10），85－107．

Engel，J．＆Sedlmeier，P．（2005）．On m iddle-school students'comprehension of randomness and chance variability in data．ZDM，Volume 37，Issue 3：168－177．

Falk，R．，＆W ilkening，F．（1998）．Children's construction of fair chances：Ad justing probabilities．Developmental Psychology，34（6），1340－1357．

Gal，I．（2005）．Towards“Probability Literacy”for all citizens：Building blocks and instructional dilemmas．In G．A．Jones（Ed．），Exploring probability in school：Challenges for teaching and learning．New York：Springer，39－63．

Goldberg，E．（1966）．Probability judgements by preschool children：Task conditions and performance．Child Development，37，157－167．

Green，D．R．（1982）：A survey of probability concepts in 3000 students aged 11-16 years．In D．R．Grey（Ed．），Proceedings of the First International Conference on Teaching Statistics，Teaching Statistics Trust，University of Sheffield，766－783．

Green，D．R．（1986）：Children's understanding of randomness．In R．Davidson＆J．Swift（Eds．），Proceedings of the Second International Conference on Teaching Statistics．Victoria，British Columbia，287－291．

Jones，G．，Langrall，C．，Thornton，C．，＆Mogill，T．（1997）．A framework for assessing and nurturing young children's thinking in probability．Educational Studies in Mathematics，32，101－125．

Konold，C．，Pollatsek，A．，Well，A．，Lohmeier，J．＆Lipson，A．（1993）．Inconsistencies in students' reasoning about probability．Journal for Research in Mathematics Education，24，392－414．

Kuzmak，S．D．，＆Gelman，R．（1986）．Young children's understanding of random phenomena．Child Development，57，559－566．

Lecoutre，M-P．（1992）．Cognitive models and problem spaces in“purely random”situations．Educational Studies in Mathematics，23，557－568．

Pange，J．（2003）．Teaching probabilities and statistics to preschool children．Information Technology in Childhood Education Annual，1，163－172．

Pratt，D．（2005）．How do teachers foster students' understanding of probability？In G．A．Jones（Ed．），Exploring probability in school：Challenges for teaching and learning．New York：Springer，171－189．

Sharma，S．（1997）．Statistical ideas of high school students：Some findings from Fiji．Unpublished doctoral thesis．Waikato University，Ham ilton，New Zealand．

Sharma S．（2012）．Cultural influences in probabilistic thinking．Journal of Mathematics Research，4（5），63－77．

Truran，K．M．（1994）．Children's understandings of random generators．In C．Beesey＆D．Rasmussen（Eds．），Mathematics Without Lim its，Proceedings of the 31st Annual Conference of the Mathematical Association of Victoria．Melbourne，356－362．

Watson，J．M．，＆Moritz，J．B．（2003）．The development of comprehension of chance language：evaluation and interpretation．School Science and Mathematics，103，65－80．

Yost，P．，Siegel，A．E．，＆Andrews，J．N．（1962）．Non-verbal probability judgement by young children．Child Development，33：769－780．

Development of Randomness Cognition in Children of 7 to 14 Years

GONG Zi-kun1HE Sheng-qing2
（1．Hangzhou Normal University，Hangzhou 311121，China；2．Beijing Normal University，Beijing 100875，China）

The present study tested 771 children aged 7～14 years in three typical tasks of randomness（0-dimension distribution；1-dimension distribution；2-dimension distribution）cognition．Results showed dynamic changes in the development of randomness cognition increased during the age of 7 to 10 years old and then decreased during the age of 11 to 14 year old．Specifically，in the 0-dimension distribution randomness cognition，the ability gradually increased between 7 and 11 years old，and then kept stable from 12 to 14 years old．In the 1-dimension distribution randomness cognition，the ability increased between 7 to 10 years old，evidently decreased at the age of 11 years old and remained stable during the age of 13 to 14 years．However，in the 2-dimension distribution randomness cognition，the ability was at low level during 7 and 14 years old．In conclusion，the present study provides new evidence for understanding the development of randomness cognition．The ability of randomness cognition dynamically changes with age（early increase and late decrease）and this developmental profile ismainly due to the development of 1-dimension distribution randomness cognition．The present results suggest that age 10 and age 11 are crucial periods of development of randomness cognition．

development，randomness cognition，0-dimension distribution cognition，1-dimension distribution cognition，2-dimension distribution cognition

B844

A

1006－6020（2016）－04－0343－09

*浙江省哲学社会科学规划课题（16NDJC004Z）；教育部人文社会科学研究规划基金项目（15YJA880020）。

**通信作者：巩子坤，男，教授，e-mail：zkgong＠163．com。

致谢：本文得到杭州师范大学赵静博士的指导与帮助，也得到张慧增博士的帮助，特致谢意。