大迎角跨音速三角翼漩涡特性及激波与涡干扰的数值模拟研究
李自启,梁斌,罗松,刘敏
(中航工业洪都,江西南昌330024)
大迎角跨音速三角翼漩涡特性及激波与涡干扰的数值模拟研究
李自启,梁斌,罗松,刘敏
(中航工业洪都,江西南昌330024)
采用对流迎风分裂格式改进形式(AUSM+)和SST两方程湍流模型结合求解三维雷诺平均Navier Stokes(RANS)方程。通过对跨音速65°后掠尖前缘三角翼的数值模拟,研究了三角翼上翼面正激波的移动情况以及涡核破裂点变化情况。计算结果与实验对比表明:采用AUSM+格式和SST两方程湍流模型结合能够准确模拟出激波结构和大迎角下空间涡结构以及激波与涡相互干扰情况。
迎风分裂格式;SST湍流模型;三角翼;激波;空间涡
0 引言
随着计算流体技术的发展,国内外工程师对亚音速阶段漩涡流动的计算研究已趋于成熟。然而,当马赫数增加到跨音速阶段,激波出现以后,激波与附面层的相互作用以及与空间涡的相互干扰使流场变得极其复杂,呈现出与亚音速阶段不同的流动现象。
由于跨音速、大攻角条件下三角翼上翼面漩涡的流动特别复杂,而当前对漩涡的形态及破裂的变化过程的模拟还不够成熟。关于翼面漩涡的初始形态以及初始分离位置,Sarpkaya[1]认为,主要为气泡型和螺旋型两种形态。关于旋涡破裂的发展演变过程,前人在实验和数值模拟两方面做了大量工作。风洞实验显示,旋涡破裂的型态是由泡型到螺旋型,最后又回到泡型。在跨音速流场中,随着迎角的增加,三角翼上出现复杂的激波[7-10],Elsenaar[11]和Hoeijmakers[12]将其归纳为2个激波系统:第一个是由于前缘涡旋转而产生的,位于涡的底部,第二个垂直于对称面,位于机翼的后缘,但是在靠近前缘涡的区域,受前缘涡发生的影响发生了弯曲。
在三角翼旋涡破裂的数值模拟方面,许多人采用通量差分分裂迎风格式,迎风耗散格式[2]主要分为矢通量分裂(FVS)和基于Riemann解的通量差分分裂(FDS)。FVS格式有较大的数值耗散、稳定性好,但是激波分辨率不高,求解粘性流动的精度较低。FDS格式的代表格式是Roe-FDS格式,该格式具有较高的间断分辨率和数值模拟精度,但是存在非物理的数值解,需要加入人工熵修正。在20世纪90年代,Liou和Stefen提出了AUSM[3](Advection Upstream Splitting Method)格式。AUSM格式的主要思想是将无粘通量项分裂为对流通量项和压力项,基于马赫数对其分别进行特征分裂。AUSM格式在CFD研究领域得到重视,并且迅速发展和完善,相继出现了AUSM+[4]。AUSM+一类格式具有较强的分辨激波、滑流等物理间断的能力,而且具有良好的保正定性,计算高速流时不会产生“Carbuncle”现象。
本文采用AUSM+格式和三步Runge-Kutta时间离散方法以及SST二方程湍流模型[5,6]数值求解定常雷诺平均的RANS方程。对尖前缘三角翼跨音速扰流进行了模拟,分析了跨音速条件下三角翼上表面涡结构、激波分布以及前缘涡和激波的相互干扰。
1 控制方程及离散方法
1.1 控制方程
笛卡尔坐标系积分形式的Navier-Stokes方程为:

其中:
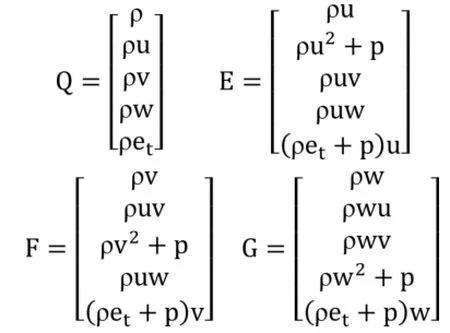
式中:Q为守恒变量;E、F、G为无黏通量;Ev、Fv、Gv为黏性通量;S为源项。
1.2 离散方法
本文中无粘性的数值离散采用AUSM+格式[4],AUSM格式的主要思想是将无粘通量项分裂为对流通量项和压力项,基于马赫数对其分别进行特征分裂。在超声速下,根据特征变量,格式具有正确的迎风方向。在亚、跨声速下,格式中需要包含所有的特征波。为了改进AUSM格式的不足,如:激波后形成“红宝石”现象,1994年Liou和Steffen[3]在AUSM格式的基础上,对该格式进行了改进,构成了后来的AUSM+格式。通量离散形式如下:

AUSM+格式中采用的马赫数分裂方法如下:
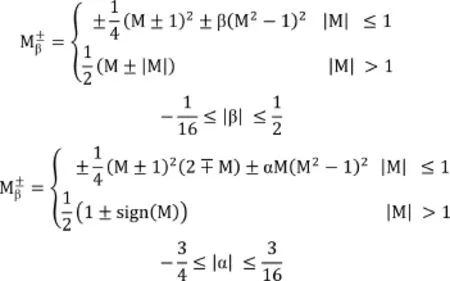
左右马赫数定义如下:

式中,C1/2为界面声速;cL为左侧网格声速;cR为右侧网格声速。
控制面处左右状态决定了格式的精度,本文采用三阶MUSCL方法插值得到计算时所用左右状态,针对于控制方程(1)中的粘性项采用二阶中心差分格式,控制方程(1)中的时间项采用三步Runge-Kutta时间离散方法。
2 湍流方程
湍流模型采用SST模型[5,6],k-ω模型求解了两个运输方程,一个关于湍动能k,另一个关于频率ω。k-ω模型的优点是可以很好的处理近壁处低雷诺数的数值计算。此模型不涉及k-ε模型中复杂的非线性衰减函数,因此计算结果更加准确,收敛性更好。低雷诺数k-ε要求近壁面处y+<0.2。而低雷诺数的k-ω模型要求近壁面处y+<2。
k方程为:

ω方程为:
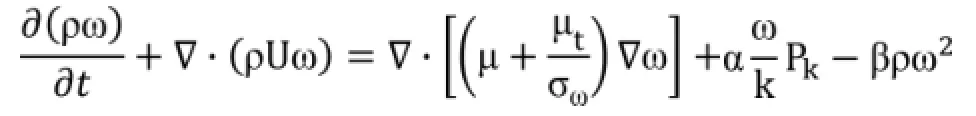
式中:Pk为湍流生成速率;模型中的常数由以下给出,即:

基于SST的k-ω方程考虑了剪切应力的传输,可以精确的预测流动的开始和负压力梯度条件下流体的分离量。SST模型的最大优点就在于考虑了湍流剪切力,从而不会对湍流粘度造成过度预测。其传输行为可由包含限制数的涡流粘度方程求得:

式中:F2是一个混合函数,其功能是用来约束壁面附面层流动的限制数。
3 几何模型和计算网格[13]
几何模型采用参考文献[13]中第四章提到的标模,机翼为65°切尖三角翼,实验数模翼型为在NACA64A005基础上将前缘用尖头的双圆弧修形。本文直接采用NACA64A005,平面参数无鸭翼,模型如图1(a)所示,根弦长为c=1.2m,后掠角为65°,展长为0.452m,稍弦长为0.239m。
计算使用的网格采用C-O型网格,网格首层高度0.001mm,网格空间增长率1.2,网格总数421万,网格拓扑结构如图1(b)。
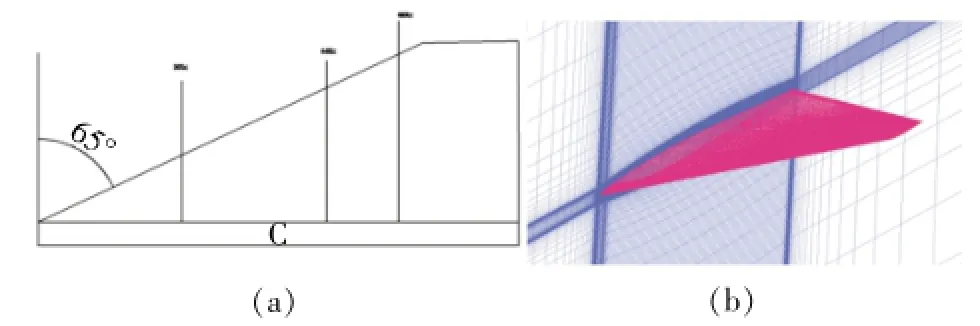
图1 几何模型与网格
4 计算结果及分析
为了更形象说明跨音速条件下三角翼空间涡的分布情况,图2和图3给出了三角翼上翼面典型空间涡的结构和三角翼上翼面表面压力分布情况。由图2可以看出,本文方法清晰扑捉出主涡、次涡以及后激波的位置。文献中采用三阶迎风格式,由图3可以看出,该方法能更清晰的扑捉正激波的位置。图4给出了截面处表面压力系数分布,由图3可知,在70%弦长以前,能够准确捕捉出横向激波的位置,70%弦长以后计算结果在机翼后缘出现了激波,导致主次涡的破裂。为了研究跨音速三角翼空间涡的变化以及空间涡与激波的相互干扰情况,选取Ma= 0.85,迎角α=19°、20°、21°、23°作为计算状态进行数值模拟。

图2 三角翼空间流动情况
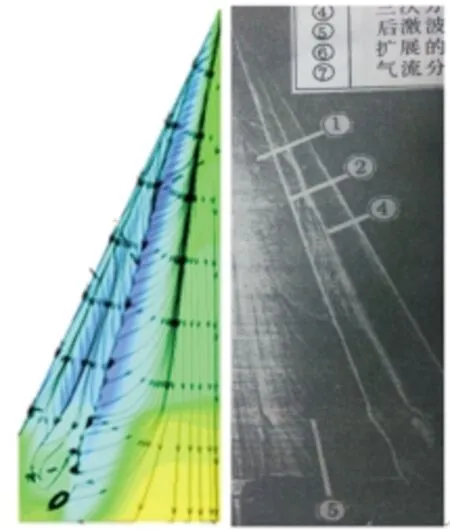
图3 计算结果与迎风格式结果对比
4.1 跨音速条件下空间涡随迎角的变化
图4给出了三角翼不同迎角下空间涡变化情况,主涡和次涡起始位置靠近三角翼尖点处,主涡和次涡在20°以前比较稳定,当迎角达到21°时,在x轴向80%左右处主涡能量变弱,次涡逐渐破裂,并且随着迎角的增加,主次涡破裂位置向前移动。
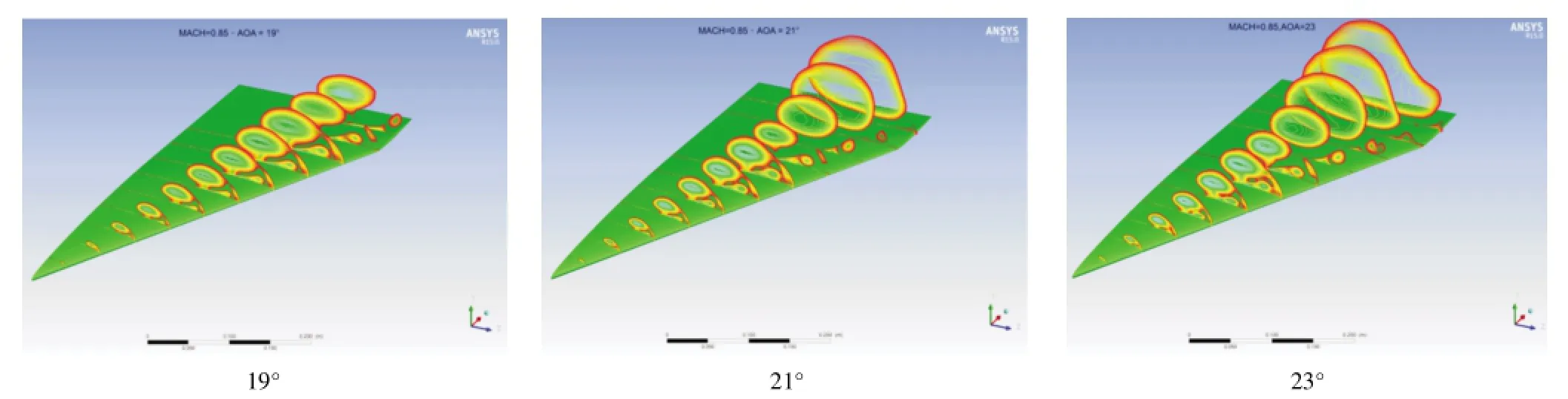
图4不同迎角空间涡变化情况
图5 给出了主涡涡核处空间流线,在21°迎角以前,涡核处的空间流线比较紧凑,此时空间涡能量强,当迎角达到21°以后,涡核处的空间流线在根弦线80%以后出现发散,此时空间涡能量变弱,并且随着迎角的增加,涡能量变弱的位置逐渐向前移动,涡轴的位置逐渐向三角翼内侧移动,涡的起点位置逐渐向三角翼尖点移动。由三角翼表面压力系数分布可以看出,随着迎角的增加,后激波位置和涡核发散点逐渐前移,由此可知,后激波将导致涡能量降低甚至破裂。
图6给出了不同截面处表面压力系数分布,在根弦线50%以前,截面压力系数分布显示,在主涡处存在较强的吸力峰值,主涡到前缘之间存在较弱的二次吸力峰值。随迎角增加,两个吸力随着涡的移动向三角翼内侧移动。
4.2 跨音速条件下空间激波随迎角的变化
图7给出了X=0.5m截面处空间马赫分布,1处激波由于主涡与二次分离区之间的横向流动,形成了一个类似收缩-扩张管的流动,局部加速到超音速,并且流动不能一直保持超音速,最终以激波减速。2处激波由于次涡顺时针旋转产生,迎角大于23°时此处出现分离。由于气流是向上加速产生的,故3处激波出现在剪切层上方,靠近三角翼前缘位置。

图5 不同迎角三角翼上空间涡线
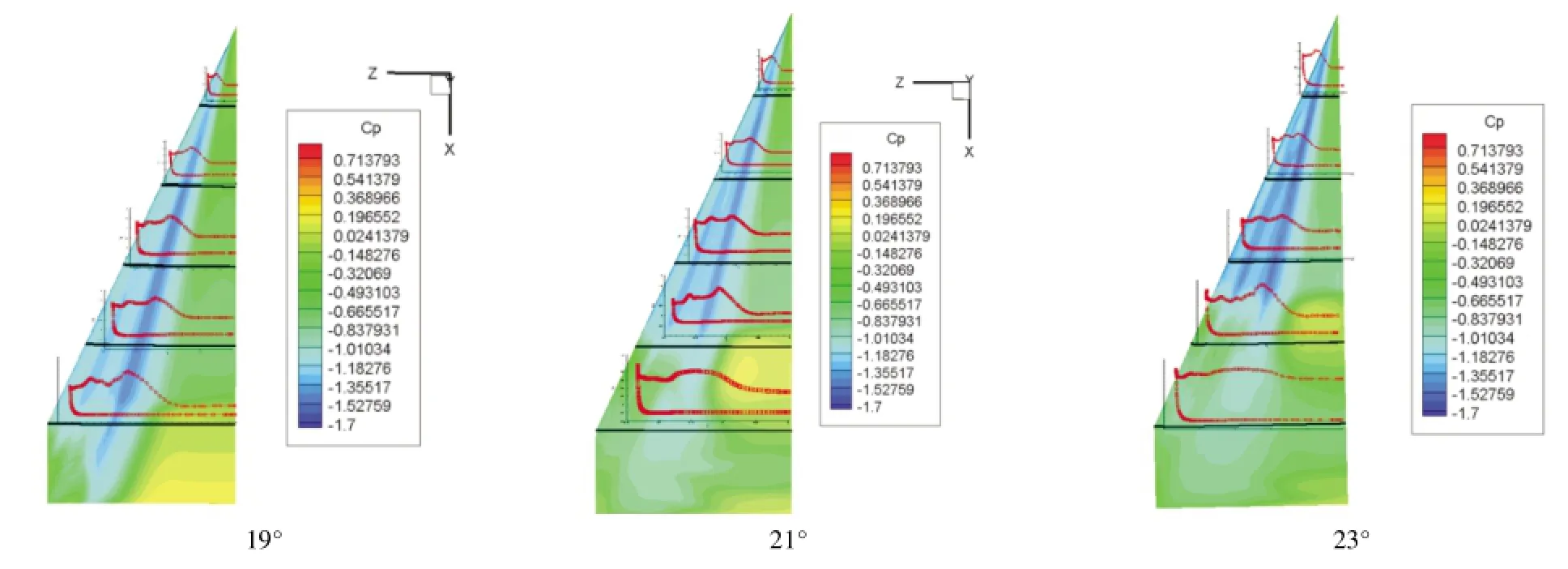
图6三角翼不同截面表面压力系数分布
图8 给出了不同迎角下三角翼上表面流线,由图可以看出,气流在三角翼前缘形成稳定的漩涡,涡迹线如1处所示,漩涡的转动在2处形成横向激波,使气流在此形成二次分离流,分离气流又形成漩涡,漩涡在贴近上翼面处形成激波,使气流在3处产生三次分离流。由于面积率和翼型的综合作用,在机翼后缘4处形成正激波。又由于激波的作用,在机翼后缘形成气流分流区,如5处。图9给出了正激波随马赫数变化情况,随着迎角的增加,激波位置逐渐前移。

图7 x=0.5m处截面展向激波分布(1、2、3为激波)

图8 不同迎角三角翼上表面流线

图9 正激波分布
5 结论
1)用AUSM+格式结合SST二方程湍流模型求解RANS方程,模拟钝前缘三角翼扰流跨音速特性。该方法准确地模拟出三角翼上表面的主涡、次涡吸力峰值以及流场中复杂流动情况,并准确地模拟出展向流动激波和正激波的位置。
2)迎角达到21°以后,三角翼后激波位置突然向前缘移动,并且与主涡发生干扰,使涡的破裂位置突然前移。
3)前缘分离涡的强度、后激波的位置以及涡轴处能量大小直接影响空间涡破裂。
4)涡能量减弱的原因是,流动空间中存在粘性,并且沿涡核移动的方向具有逆压梯度,尤其是涡核处,逆压梯度更大,会导致涡能量减低甚至破裂。
[1]Sarpkaya T.On Stationary and T raveling Vortex Breakdown[J].J.Fluid Mech.,1977,45(3):545-559.
[2]Steger J L,Warming R L.Flux vector splitting of the inviscid gas dynamic equations with application tofinitedifferencemethods[J].Journalof Computational Physics,1981.40(2):263-293.
[3]Liou M S.Ten years in the making AUSM family[R].AIAA Paper 2001225212CP,2001.
[4]Liou M S.A sequel to AUSM:AUSM+[J]. Journal of Computational Physics,1996,129(2):364-382.
[5]Hellsten,A.New Two-Equation Turbulence Model for Aerodynamics Applications[D].Department of Mechanical Engineering,HelsinkiUniversity of Technology(Espoo,Finland),2004.
[6]Wallin,S.and Johansson,A.V.An Explicit andAlgebraicReynoldsStressModelfor incompressible and Compressible Turbulent Flows[J]. Journal of Fluid Mechanics,Vol.403,2000,pp.89-132.
[7]Drougge,G.The International Vortex Flow Experiment for Computer Code Validation[J].ICAS Proceedings,1988,Vol.1,pp.35-41.
[8]Elsenaar,A.Hjelmberg,L.Bütefisch,K.-A., and Bannink,W.J.,The International Vortex Flow Experiment[?].AGARDCP 437,Vol.1,1988,pp.9-1 to 9-23.
[9]Londenberg,W.K.,Transonic Navier-Stokes Calculations About a 65 Degree Delta Wing,NASACR-4635,Nov.1994.
[10]Chiba,K.and Obayashi,S.,CFD Visualization of Second Primary Vortex Structure on a 65-Degree Delta Wing,AIAA Paper 2004-1231,Jan.2004.
[11]Erickson G E,Rogers L W.Experimental study of the vortex flow behaviour on a generic fighter wing at subsonic and transonic speeds.AIAA-1987-1262.1987
[12]Donohoe S R,Bannink W J.Surface reflective visualisation of shock-wave/vortex interactions above a delta wing.AIAA Journal,1995,33(4):680-687.
[13]方宝瑞.飞机气动布局设计[M].北京:航空工业出版社,1997.
[14]朱自强.现代飞机空气动力学[M].北京:北京航空航天大学出版社,1982.
>>>作者简介
李自启,男,1985年1月出生,2013年毕业于南京航空航天大学,现从事气动布局设计工作。
Study on Vortex Features of Big-elevation Angle Transonic Delta Wing and Numerical Simulation of Interference of Shock Wave and Vortex
Li Ziqi,Liang Bin,Luo Song,Liu Min
(AVIC Hongdu Aviation Industry Group,Nanchang,Jiangxi,330024)
The combination of AUSM+(Advection Upstream Splitting Method)and SST two-equation turbulence model are used to solve three-dimension Navier Stokes(RANS)equation.With the numerical simulation of transonic sweptback leading-edge delta wing of 65°,study on movement of normal shock wave on the wing upper surface of delta wing and change of vortex fracture point has been done.The calculation result and test comparison show that the combination of AUSM+and SST two-equation turbulence model can accurately simulate structures of shock wave and space vortex at a big elevation angle,as well as interference of shock wave and vortex each other.
upstream splitting method;SST turbulence model;delta wing;shock wave;space vortex
2016-01-13)

