基于层次分析法的房地产选址因素评价

韩沙鸥

(四川水利职业技术学院，四川 崇州，611231)

基于层次分析法的房地产选址因素评价

韩沙鸥

(四川水利职业技术学院，四川 崇州，611231)

随着社会经济的发展，收入水平的增加，消费者对商品住房的有效需求也在增加。针对消费者的需求，房地产开发商也在不断地推出新的楼盘，商品房价格、周围环境、使用面积、户型等各有不同。消费者对于楼盘的选择，决定着房地产商的资金回收，可见房地产位置的选择对于开发商来说至关重要。本文通过对影响房地产选址主要因素的分析，运用层次分析法，建立房地产选址方案的优化选择模型，确定优先顺序，从而为决策者正确选址提供定量分析依据。

房地产 层次分析法 评价 选址因素

1 引言

房地产项目选址的研究已经开展了相当长的时间，国内外学者从不同角度、采用不同的方法进行研究，形成了一些常规的选址模型。如文献〔1〕采用灰色系统理论，通过建立多层次灰色评价模型进行房地产开发项目选址的研究。文献〔2〕采用特尔菲法进行房地产开发项目选址研究。文献〔3〕通过构建选址的评价指标体系，运用粗糙集的相关理论，通过建立选址集合模型进行房地产项目选址的决策分析。文献〔4〕采用模糊意见集中决策的方法，通过对方案集合中的对象进行排序，得出最佳选址方法进行房地产项目选址的研究。文献〔5〕通过实例，分析房地产开发项目选址影响因素，阐述了GIS在房地产开发项目选址中的应用。文献〔6〕从定性的角度提出房地产开发区位选择的原则，阐述了居住用房地产和商业用房地产选址时各自所应侧重的方面，使区位选择更加具有操作性。文献〔7〕分析了层次分析法在生态环境质量综合评价指标权重确定中的应用，并论述了层次分析法应用于生态环境质量综合评价中的优劣性。文献〔8〕主要对住宅房地产开发区位选择提出策略及建议，为企业在投资开发不同类型项目时提供区位选择的参考意见。文献〔9〕从影响房地产住宅项目选址决策的评估指标入手，构建了选址决策模型。通过该模型的运用可以为房地产开发企业提供一个科学、合理的选址决策结果。

房地产的选址工作是每一个房地产企业都必须面临的一件重要工作。由于各个备选方案情况不同，其地块成本、维护成本、周边环境、交通的便利性、周边竞争对手的多少等会有所不同，所以房地产的选址是一项复杂的工作。如何从若干个房地产选址备选方案中选择一个最佳方案，对企业的成败，尤其是对一些规模较小的房地产企业来说至关重要。本文通过层次分析法，确定方案选择中各个要素的重要程度，以此来为房地产商提供选址依据。

2 房地产选择原理

2.1 房地产选址方案评价体系的建立

房地产选址决策是一个复杂的决策问题，涉及备选方案的产业政策、区域区位特征、交通运输发展状况、周边配套设施状况等多方面因素。本文将综合考虑这些因素，通过建立房地产选址决策模型，运用层次分析法对选址方案进行综合评定。一般而言，评价一个房地产企业的选址是否合理，可以从经济性、便利性、竞争性等方面综合考虑，具体评价指标如表1所示。

2.2 房地产选址方案选择模型的构造

2.2.1 基本假设

假设条件1：受评方案均满足房地产选址方案的优化选择模型的基本要求；

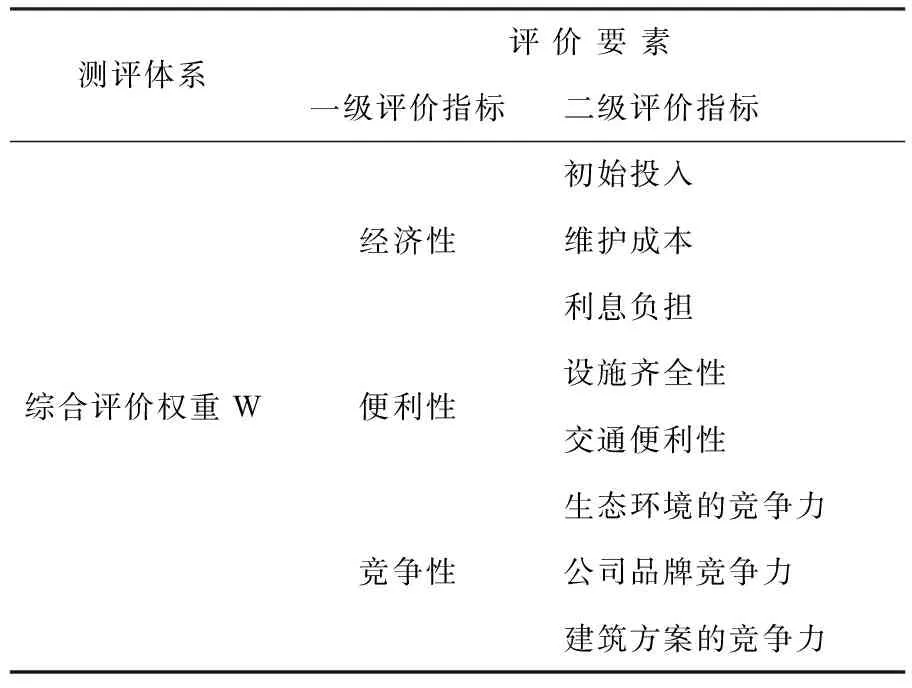
表1 房地产选址方案选择评价体系

假设条件2：评分专家对所评方案的评分是客观和公正的，且对指标无明显偏好；

假设条件3：权数越大，则该房地产选址方案越优。

2.2.2 建立层次结构模型

首先根据多目标决策问题的性质和总的目标，对所要解决的问题有明确认识，弄清问题的边界、包含的因素以及因素之间的隶属关系，将决策问题层次化，构造一个自上而下的层次结构模型。

2.2.3 构造判断矩阵

判断矩阵的构造是指在层次结构模型中，针对上一层次某元素来说，本层次有关元素之间相对重要性的比较。有决策人或专家组根据该企业的具体情况与企业对渠道成员的实际要求，通过对两两因素的比较，用表2的标度打分，可以得到判断矩阵。

表2 判断矩阵1-9比率标度及其含义

2.2.4 层次单排序

层次单排序是指根据判断矩阵计算对于上一层元素而言，本层次与只有联系的元素相对重要性次序的权重。层次单排序需要计算判断矩阵A的特征根和特征向量，即满足A·W=λmax·W(取正规化特征向量)，其分量Ai为相应元素排序的权值。计算判断矩阵特征根的方法很多，本文采用和积法，其计算步骤为：

(1)将判断矩阵A的每一列正规化，即

(i，j=1，2，…，n)

(3)对Wi归一化；

(4)计算判断矩阵的最大特征根：λmax；

(5)一致性检验。

为检验判断矩阵的一致性，需要计算它的一致性指标CI和随机一致性指标RI。

CR=CI/RI

式中，n为矩阵阶数。RI值如表3所示。

表3 平均随机一致性指标RI

当CR<0.1时，即认为判断矩阵具有满意的一致性，否则需要调整判断矩阵，使之具有满意的一致性。

2.2.5 层次总排序

利用同一层次中所有单排序的结果，就可以计算针对上一层次而言，本层次所有元素相对重要性的权重，即层次总排序，并进行一致性检验。

3 评价体系的应用

某房地产公司想把羊马河附近打造成水景原生态住宅，该决策主要根据经济性、便利性和竞争性三大准则来进行评选，具体包括初始投入、维护成本和交通便利性等8个指标。

3.1 建立层次结构模型

层次结构模型如图1所示。

3.2 构造判断矩阵

根据专家判断，构造判断矩阵，进行层次排序，并对判断矩阵做一致性检验。

3.2.1 判断矩阵的构造(如表4所示)。

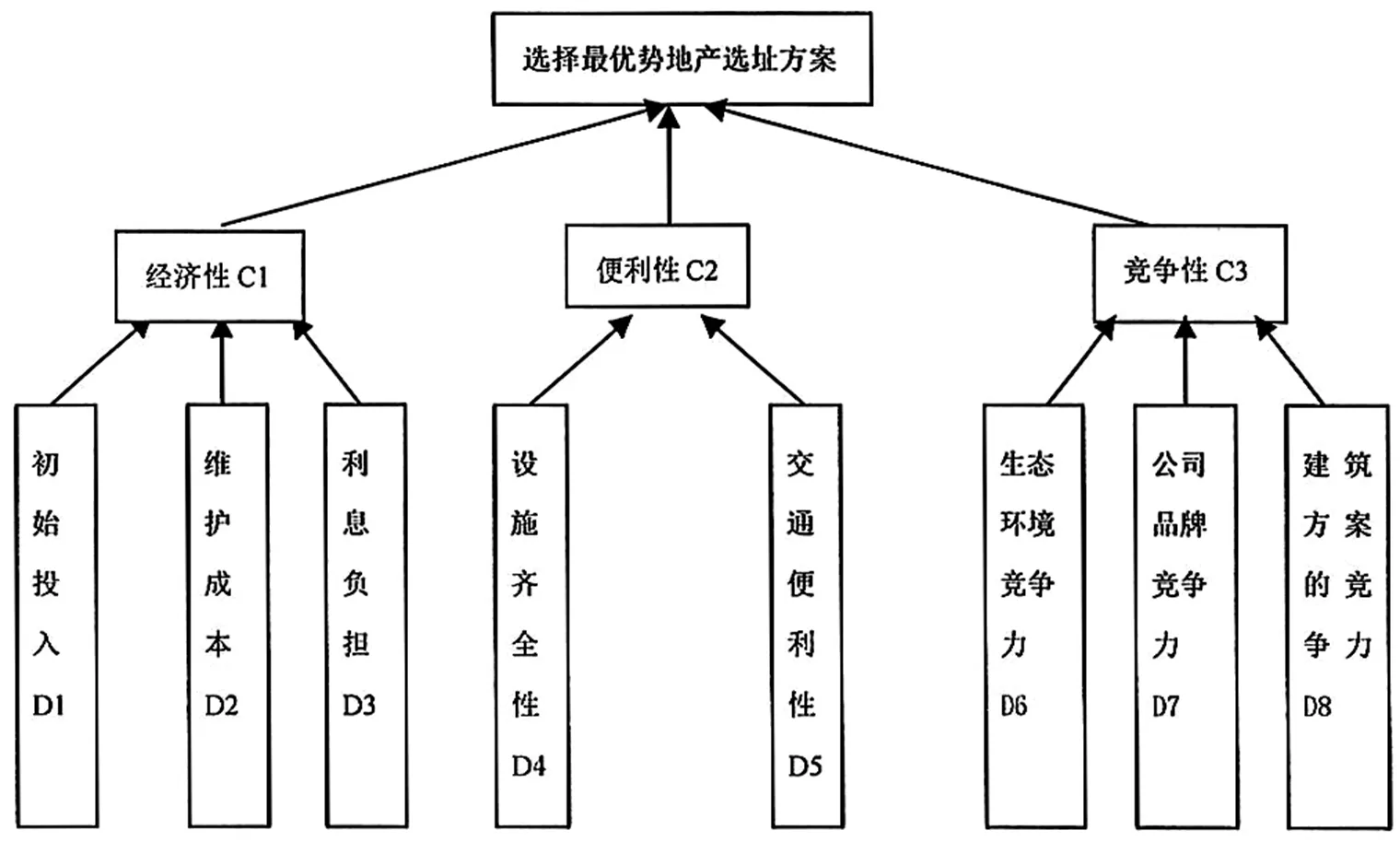
图1 层次结构模型

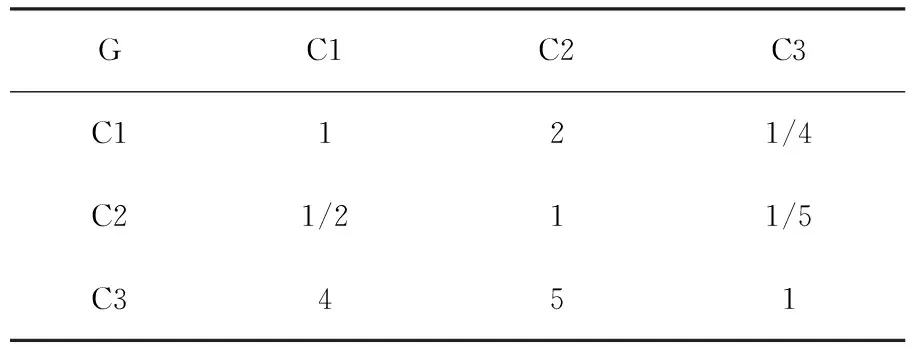
表4 矩阵表

3.2.2 就判断矩阵计算权数的单排序，并进行一致性检验

按前述步骤，计算判断矩阵中各评价指标对最优选址的重要性权数。于是，对于C-G(准则层相对于目标层)的权向量计算如下：WG1=1/3[1/(5+0.5+2/8+(1/4)/(1+9/20))]=0.201，同理算出WG2=0.118，WG3=0.681。

所求特征向量(权数)WG=[0.201，0.118，0.681]。

计算判断矩阵的最大特征根λmax。

判断矩阵的一致性检验：

G-C=(3.022-3)/(3-1)=0.011

查表，当n=3时，RI=0.58；则CR=CI/RI=0.011/0.58=0.019，即CR<0.1，认为判断矩阵有令人满意的相容性，即经济性对最优选址最重要(0.607)；便利性其次(0.354)；竞争性次之(2.075)。

3.2.3 根据以上步骤，可以分别计算出C—D判断矩阵方案重要性、权数和最大特征值、检验值等结果。

判断矩阵C1～D到C3～D(表5，表6，表7)。

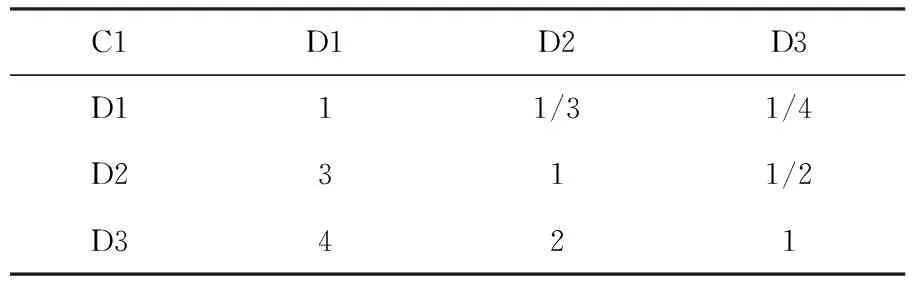
表5 矩阵表

表6 矩阵表

表7 矩阵表

计算特征向量、最大特征值、检验值如下：

WC1=[0.123，0.320，0.557]，λmax=3.019，CI=0.0095，RI=0.58，CR=CI/RI=0.016<0.1；

WC2=[0.25，0.75]，λmax=2，RI=0，CI=0.3；

WC3=[0.648，0.122，0.223]，λmax=3.015，CI=0.0075，RI=0.58，CR=0.0129<0.1。

3.3 进行层次总排序，得出决策结果

按照上述求CW的方法，同样可以求出方案层对目标层的排序权重分别为：0.025，0.064，0.112，0.030，0.089，0.441，0.083，0.152。然后进行总排序的一致性检验。

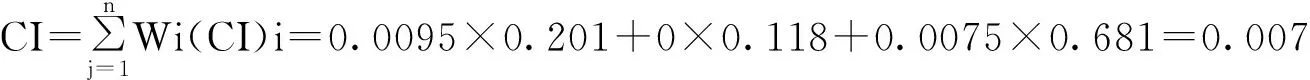
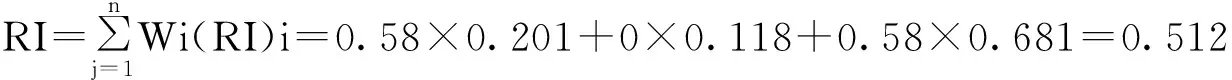
CR=CI/RI=0.007/0.512=0.014<0.1，可以认为层次总排序结果具有满意的一致性。

从上可知，在这八个指标中，生态环境对选址方案影响最大，其次是建筑方案的竞争力，利息负担，交通便利度，公司品牌竞争，维护成本，设施的齐全性和初始投入。经过计算将指标进行排序，排出了重要程度，对于房地产开发商有很重要的参考价值。

4 结论

综合以往房地产选址来看，大多数的房地产选址都是从定性的角度进行描述，带有一定的模糊性和主观性。而本文构建的房地产项目选址决策模式，为房地产开发企业提供了一种行之有效的选址决策方法。该决策模式通过对影响房地产选址主要因素的分析，运用层次分析法，建立房地产选址方案的优化选择模型，确定优先顺序，为决策者正确选址提供定量分析依据。同时，在运用过程中能弱化决策者的主观影响，不仅是定量确定各评价指标相对重要性的有效手段，而且使最终决策结果更加科学、合理，更具说服力。

〔1〕郜振华.灰色系统理论在房地产项目选址中的应用[J].价值工程，2005，(11)：50～52.

〔2〕邹金秋，张根寿.基于特尔菲法的房地产开发项目选址研究[J].华中农业大学学报，2002，(2)：73～76.

〔3〕黄正军，万继业，李化民.基于集合理论的房地产项目的选址决策分析[J].重庆大学学报(自然科学版)，2007，(9)：113～116.

〔4〕唐 轶.模糊意见集中决策在房地产项目选址中的应用[J].山西建筑，2007，(27)：243～244.

〔5〕吕海峰，韩 滨.基于空间叠加分析方法的房地产开放项目选址的研究[J].中国新技术新产品，2009，(18)：226～227.

〔6〕施建刚.房地产开放项目区位因素分析与研究[J].华东经济管理，2001，15(4)：101～104.

〔7〕李 恺.层次分析法在生态环境综合评价中的应用[J].环境科学与技术，2009，32(2)：183～185.

〔8〕孙 艳.住宅房地产项目开发区位选择策略[J].现代商贸工业，2009，(19)：23～24.

〔9〕张 巍，胥维桃，郑增枫.住宅项目选址决策模型[J].重庆大学学报(自然科学版)，2007，30(8)：153～158.

■

O212.4∶TU

B

2095-1809(2016)04-0100-04

韩沙鸥(1988-)，女，四川彭州人，硕士，助教，主研测量和地理信息系统。