利用一题多变策略分析等价无穷小量的误用

宋鹏翔 郑立飞 吴养会

（1.海军航空工程学院青岛校区 山东 青岛 266000 2.西北农林科技大学理学院 陕西 杨凌 712100）

众所周知，学生在学习极限并计算极限的时候，等价无穷小量的误用是经常的事情。这个地方的错误率非常高，尽管主讲老师多次强调，等价无穷小在加减的时候不可以随意使用，但是学生的作业，考试中此类错误仍旧频频出现。另外，“一题多变”可以逐渐深入，举一反三，开发学生思维，扩散学生的思维，培养学生思维创造能力[1-5]。利用“一题多变”的策略进行教学，可以使学生对所学的知识达到活化、深化和融会贯通，

解：

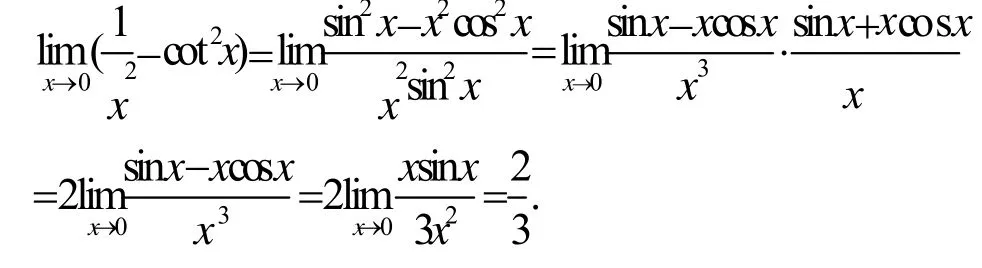
有的学生提出：能否将上题第一项的分母换为相应的等价量 sin2x，而得到相同结果呢？由此，得到下述变化的题目：

这个题目的解法如下：从而培养他们的创新思维能力。为此，在给学生讲课的时候，针对一个作业题，笔者重点对其进行了一题多变，由此告知学生：等价无穷小在求极限的时候一定要注意使用条件。

笔者在黑板上讲解的原题为：

首先给出此题的正确解法：

显然结果并非正确答案，从而说明极限式的分子中的第一项不可以换为 sin2x.

有学生又问，原题既然可以写为

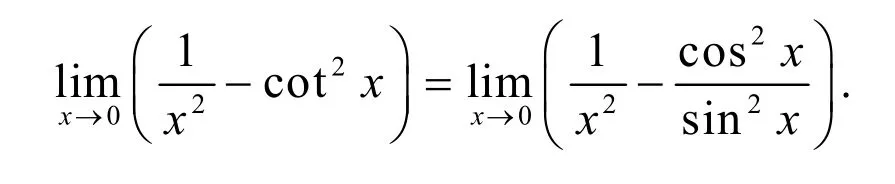
这个等式右边的第二项的分母能否换为x2，换了后结果一样吗？由此得到如下的题目：

显然结果并不是正确答案。

对变化 2的题目进一步改造，就得到如下题目：

解：

上述题目的各种变形说明：利用等价无穷小量求极限的时候，初学者一定要注意该方法的适用范围。一般而言，等价无穷小量只在乘除的情况下使用，不主张在加减的情况下使用其求极限，否则，会导致各种不同的极限值。如果为了进一步提高学生的研究能力，可以给出如下解法：

以上是用无穷小代换把cosx换成二次多项式。可以进一步思考的是，究竟用二次多项式替换还是一次或更高次多项式替换好，值得初学者思考。

显然，结果不对，这里也用的是等价无穷小代换，为什么就得不到正确的结果呢？

前几次变式用等价无穷小替换其实就是一阶

结果显然还是不同。

同样，将第一项的x2换为 tan2x后，给出如下的题目：

变化4：计算

结果再次发生变化，还是错误的结果。

泰勒公式展开，由于精确度较差，有些题无法解决，此时可以尝试使用泰勒公式展开得到更高阶数来求解。

上述做法也说明，当课堂教学中遇到学生容易产生错误做法的内容时，教师不妨利用一题多变来对相应的问题进行解析，这样更容易让学生看到问题的本质，从而更好地理解相关知识，达到大学数学教学的目的。