2种常见数学模型在智能仪表校验中的应用

王小杰

（河南省中原大化集团有限责任公司，河南 濮阳457004）

经验交流

2种常见数学模型在智能仪表校验中的应用

王小杰

（河南省中原大化集团有限责任公司，河南 濮阳457004）

针对变送器校验过程中由于数据分析处理不当导致校验结果不准确的问题，提出了2种常见数学模型对校验数据进行分析的方法。1种为2点确定1条直线法即理性曲线模型，1种为多点线性回归确定直线法即拟合曲线法。同时，以1台精度等级为0.2级变送器校验数据为例详细介绍了2种化工生产过程中常见的校验分析方法，得出了针对不同类型不同精度等级的仪表校验时究竟采用何种模型更为合适，需要具体情况具体分析的结论，为不同方法得到矛盾结论提供了理论依据。

数学模型；仪表校验；应用；理想曲线；拟合曲线

在连续的化工生产过程中，智能型模拟变送器的线性度会随着传感器的疲劳或者信号处理单元电子元件所处高温等环境带来的温度漂移而逐渐降低，测量误差随之增大。为了检验变送器是否仍能达到所需精度等级，仪表工通常借设备大修之际或者定期将操作工反应误差较大的仪表进行拆回校验处理[1]。在校验过程中，对数据进行分析时常采用2种常见数学模型判断仪表精度等级。1种是根据零点、量程确定一条直线，即变送器理想特性曲线进行判断；另1种是根据零点、量程和中间选取的几个点按照线性回归方程确定1条直线，即拟合特性曲线进行判断。

1 智能型仪表的基本数学模型

智能型仪表通过传感器将被测过程变量如压力、流量等工艺参数转换为电信号后，再经过运算放大等信号处理转化为4～20 mA线性输出[2]。因此，智能仪表基本数学模型可表示为：

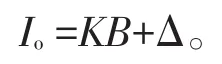
式中，Io为输出电流（4～20 mA），K为转换系数，B为被测变量压力、流量等，Δ为零点漂移值。

根据2点确定1条直线的基本数学原理，通过设置仪表零点、量程确立的输出特性曲线，称为仪表理想特性曲线模型。当被测变量为零（量程下限）时仪表对应输出信号4 mA；当被测变量为量程上限时仪表对应输出信号20 mA；当被测变量为量程范围以内其他值时，仪表输出对应于零点、量程确定的直线上的各相应点。

对于智能模拟型变送器，其输出与输入之间存在着线性相关的关系，在仪表校验时实验所得数据分布在某一直线周围。通过线性回归方程求得该直线的方法，通常称为仪表拟合曲线模型[3]。对于拟合曲线，当被测变量为零（量程下限）时仪表对应输出信号不一定为4 mA，当被测变量为量程上限时仪表对应输出信号不一定为20 mA，但均位于拟合线性回归直线周围。

2 2种不同模型的应用

不论是2点确定1条直线还是利用线性回归方程拟合直线，在平常仪表校验工作中均有应用。不同的人员对不同的仪表采取不用的数学模型进行数据分析，得到的校验结轮也就可能存在较大出入。因此，在仪表校验工作中仪表工除了需要具备一定的实际操作能力，还应掌握必要的数据分析技能。

2.1 理想特性曲线

对于一般的压力变送器等通常只需要设置量程等参数就可以开始校验，如果零点存在漂移的情况，则可以通过手操器进行清零处理。然后在变送器信号回路中串入电流表逐渐增大输入信号，记录电流表测量的变送器输出电流。通常记录量程的0%3、6245.%、50%、75%、100%等5点的输出值进行记录并以此分析变送器是否满足精度等级要求。

按照理想特性曲线以上5个输入点对应的电流输出值应分别为4、8、12、16、20 mA。将实测值与理想值相减得到相应的误差值，根据各点误差最大者判断是否在仪表精度等级所允许误差范围内。如果在误差允许范围内，则认为该仪表为合格，否则不合格。对于不合格仪表通常采用降级使用或者淘汰处理。

2.2拟合特性曲线

二变量线性回归方程为：

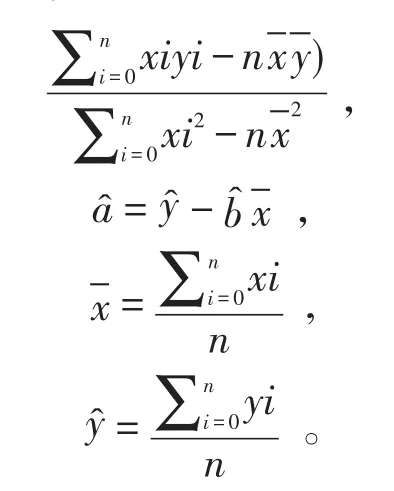
3 应用实例

假设现场1台普通导压管式差压变送器量程为0～20 kPa，工艺反应指示不准，按照生产要求需将其拆回校验处理。调好零点后通过加压实验，得到数据如表1所示。

表1 13PDT-0065校验数据Tab 1 Calibration data of 13PDT-0065

采用拟合曲线模型对仪表进行校验的步骤与理性曲线模型基本一致，不同之处在于在得到各点数据后需要通过线性回归方程得到拟合直线并计算各输入值对应直线上的输出值，然后将测量值与线性回归直线上的值相减得到误差值，判断仪表合格与否的方法与理性曲线模型一致。

线性回归方程算式复杂，计算起来更是繁琐，稍有不慎很容易计算错误，如此一来得到的校验结论也就变得不可靠。因此，对校验师傅而言，在对仪表进行校验时更乐意采用理想型模型对数据进行分析。

相比而言，拟合曲线模型比理想曲线模型具有更强的说服力。随着计算机技术的不断普及，免去了人们很多脑力计算的烦恼。办公软件Excel的曲线拟合功能为广大仪表工进行校验数据分析带来了极大便利。只需将校验过程中得到的数据输入Excel中，然后通过拟合曲线的方法就可以能够轻松获得所需要的曲线[4]。当然，对于检验中存在的粗大误差等需要用误差分析中的3σ法则等手段首先予以排除[5]。

根据校验所得的实验数据按照理想型曲线Io= 0.8B+4计算误差及回差数据如表1所示，如果变送器精度等级要求为0.2级，则其最大允许误差为0.032 mA。从表1可以看出，最大回程误差为0.040 mA，已超出允许范围，故该变送器不合格。

根据校验所得的实验数据通过Excel拟合曲线的方法得到上升拟合曲线方程为Io=0.795B+4.024，下降拟合曲线方程为Io=0.797B+4.008，计算误差及回差数据如表1所示。从表1可以看出，最大回程误差为0.026，在仪表最大允许误差范围内，故该变送器合格。

4 结束语

相同的一组原始校验数据采用不同数学模型进行分析得出的结论迥然相反，按照理想模型分析得出的结论是仪表不合格，而按照拟合直线方法得到的结论为仪表合格。因此，针对不同类型不同精度等级的仪表校验时究竟采用何种模型更为合适，需要具体情况具体分析。正如范例所示，如果差压式变送器改为液位测量时，则0.5级精度完全能够满足工艺生产需要，此时按照理想曲线模型分析时也不会有任何问题。

[1]朱静山.浅谈智能差压变送器的校验[J].化工管理,2013 (2):35-36.

[2]乐嘉谦.仪表工手册[M].北京：北京工业出版社,1998:80-82.

[3]盛骤,谢式千,潘承毅.概率论与数理统计[M].4版.北京:高等教育出版社,2008:105-108.

[4]陈雄新.利用Excel软件做统计描述和方差分析的方法[J].湖南生物职业技术学院学报,2008(3):28-29.

[5]费业泰.误差理论与数据处理[M].6版.北京:机械工业出版社,2010:70-75.

TQ056.1

BDOI10.3969/j.issn.1006-6829.2016.03.011

2016-03-24