基于地下水数值模拟的地球物理反演解释优化方法研究*

李学兰董艳辉李帝铨③

（①中南大学，地球科学与信息物理学院 长沙 410083）

（②中国科学院地质与地球物理研究所 北京 100029）

（③中南大学，有色金属成矿预测教育部重点实验室 长沙 410083）

基于地下水数值模拟的地球物理反演解释优化方法研究*

李学兰①董艳辉②李帝铨①③

（①中南大学，地球科学与信息物理学院 长沙 410083）

（②中国科学院地质与地球物理研究所 北京 100029）

（③中南大学，有色金属成矿预测教育部重点实验室 长沙 410083）

地球物理的多解性无处不在，面对这种情况我们往往结合地质资料来对反演结果进行合理的地质解释。然而在偏远地区地质、深部钻探资料非常缺乏，野外已有的井孔也往往难以获取岩性编录资料。当这些资料比较少时，反演结果依然存在难以解释或者不确定等问题。是否可以借助于地下水位与水质信息包含的地质体水力特性，来辅助地球物理反演过程？基于此思路探索了基于地下水模型的地球物理反演解释优化方法：以大地电磁法为实现手段，通过研究已知理想地质模型和多个基于反演结果解释得到的地质模型，建立地下水数值模型，对比地下水水流和溶质运移数值模拟结果，最终确定相对最佳地质模型。并通过敏感性分析验证了运用地下水数值模拟搜索相对最佳地质模型的可行性。

地球物理反演 地质模型 地下水流动数值模拟 溶质运移

0 引 言

地球物理资料的反演和解释（王家映，2002）是用来了解地球内部物理性质以及矿产资源分布的。在科学研究和工程技术领域中，凡是涉及根据观测数据推求模型或者体系时，都无法回避反演问题（魏超等，2008）。目前，自然地质活动与人文地质活动不断增加，使得目标体所处的地质环境越来越复杂，使用传统单一的地球物理探测方法并不能很好地获得高质量的野外采集数据，加上各类地球物理方法都具有一定的局限性（陈思宇，2014），如：电法（电磁法）勘探分辨率的高低往往受探测深度的影响，有时获得地质体异常响应可能会表现出信号微弱、轮廓不清晰等特点（戴前伟等，2013），屏蔽层的存在使得地震勘探也无能为力，空间分布特征的探测对地球物理测井也是一种挑战，非唯一性对重力及磁法勘探的影响更不容小觑。单一地球物理勘探方法的局限性及场的等效性是造成反演问题多解性的一部分，它是无法避免的。除此之外，地球物理问题反演多解性与野外数据采集过程中噪声强弱、仪器精度高低、数据量多少等因素也息息相关，这些因素均影响了地球物理勘探成果的可靠度。

针对反演问题的多解性，解决方案通常有两种。其中之一是通过已有的可靠的地质信息来约束地球物理反演过程，引导反演过程趋于合理、趋向真实的野外地质情况（郭冬等，2014）。它是指对于先验地质信息确定的单元，迭代时保持其物性资料的不变，即在目标函数中引入含有先验地质信息项，得到考虑数学和地质合理性的反演结果（Yeh et al.，2002；祁光，2013；陈思宇，2014）。它能降低反演非唯一性，提高分辨率，但是先验地质信息往往比较匮乏，在这种情况下尽可能扩大数据量，从数学角度出发，让反演方程不断趋向完善与合理是行之有效的一种方法（郭冬等，2014）。因此众多学者在某些经典算法上进行改进（魏超等，2008；Yuan et al.，2009），如魏超等（2008）提出了基于量子蒙特卡罗的地球物理反演方法，这种方法适合于非线性、多极值的地球物理反演问题，在收敛速度和避免陷入局部极小等方面有着一定的优势，具有较强的通用型，但是基于量子蒙特卡罗的反演方法中试探波函数以及动能项的设置是根据量子系统来设置的，对于实际地球物理反演问题而言，这种设置可能并不那么合理。与此同时，地球物理联合反演（敬荣中等，2003；于鹏等，2006；何委徽等，2009；Wu et al.，2012）被广泛应用于反演中，其实质为数据融合。联合反演发展主要分为以下两个方向，其一为已知地质信息和地球物理模型统一起来的联合反演，或者是不同地球物理勘探方法所得观测数据之间的联合，如地震和电法，地震和重力，重力和大地电磁法等，但是不同物性之间存在着相关的内在联系是联合的基础（林达明等，2014），通过这种方法能达到相互约束、补充的目的，从而减小反演多解性。其二为数学、地质、地球物理模型统一起来的联合反演，它利用波动场和扩散场间的相互联系，通过数学变换，建立多种地球物理勘探方法的数学物理模型，并将其统一起来，得到共同数学物理模型，从而进行统一的反演成像（陈洁等，2007）。联合反演使得反演结果有更高的分辨率，并能较好地解决非唯一性问题，但其要紧密结合岩石物理性质的统计规律，才能取得兼容地质与综合方法的应用效果（杨文采，2002）。尽管不同的地球物理反演方法均有一定的局限性，但是随着反演约束条件的增加，反演所得的结果与真实情况的吻合度逐渐增加。源于电流场与渗流场的相似性（喻永祥等，2006），地球物理与地下水紧密结合在一起。目前已有学者尝试用各种地球物理方法来间接求取渗透系数，如喻永祥等（2006）实现了运用高密度电阻率成像法获得非均质多孔介质的渗透系数。Andersen et al.（2013）将地下水与地球物理模型结合起来研究山谷流域的捕获区、补给区、地下水年龄，尽管文中指出不能太依赖地球物理反演结果，但是它对本文的研究有很好的启发性。Singha et al.（2006）提出了一种建立电阻率与浓度物性关系的方法，通过物性关系可以将电磁法中所得反演剖面转换成浓度剖面，很好地从反演结果中提取了地下水的相关信息。Yeh et al（2002）提出了将先验地质信息引入到反演中，并由电阻率得出美国新墨西哥州索科罗STVZ区域含水分布曲线。

当地质资料特别是钻探资料丰富时，地球物理反演结果可以得到较好的优化，可以得到地层结构较准确的刻画。但在偏远的、缺少地质资料地区，深部钻探资料非常缺乏，野外已有的井孔也往往难以获取岩性编录资料。由于地质体的水力特性，如渗透系数，与地层岩性有着直接关联，那么，是否可以通过地质体中的地下水系统循环特征，如水位、水质信息来反应地层岩性并辅助地球物理反演解释呢？基于此思路，本文以大地电磁法为实现手段，探索地质数据缺乏时，基于地下水模型优化地球物理反演解释的方法，通过已知理想地质模型及敏感性分析来验证运用地下水数值模拟搜索相对最佳地质模型的可行性。

1 研究方法

1.1 地球物理正反演

地球物理正演是给定场源的分布，求解场值的大小。反演是正演的逆过程，即由场源观测数据求出场源的物性分布（徐世浙，1994）。如果把模型空间中的一个点定义为m，把数据空间中的一个点定义为d，按照物理定律，可以把相关关系写成：

其中，G为模型空间M到数据空间D的一个映射。从式（1）、式（2）可知正演是从模型空间到数据空间的过程，反演是从数据空间到模型空间的过程。用流程图描述如下（图1）：

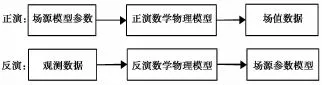
图1 正反演流程图Fig.1 The flowchart of forward and inversion

1.2 地下水数学模型与数值求解

1.2.1 地下水流动数学模型及数值方法

依据三维地下水流动的水文地质概念模型，地下水三维非稳定流方程可以描述为（Panday et al.，2013）

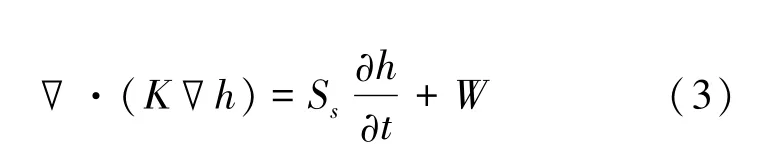
式中，K为渗透系数；h为水头高度；Ss为储水系数；t为时间；W为单位体积的源汇项，上述数学模型采用的数值解法为有限差分法（陈崇希等，2009）。

1.2.2 溶质运移数学模型及数值方法

饱和带溶质运移的对流－弥散方程为（薛禹群等，2007）

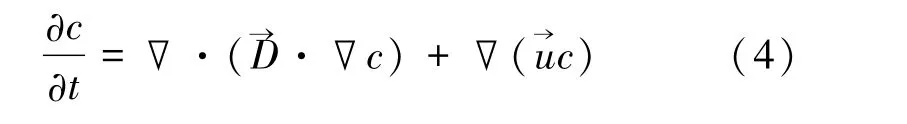
式中，c为溶液中某种组分的浓度；→u为实际平均流速矢量；→D为水动力弥散系数。大多数解决溶质运移的数值方法为欧拉法、拉格朗日法、欧拉—拉格朗日混合法，详细求解可参考（Zheng et al.，1999）。

1.3 基于地下水数值模拟的地球物理反演解释优

化方法

为了了解地球内部物理性质及其矿产资源分布（魏超等，2008），往往会通过地球物理资料的反演来对其进行合理的解释，电法、电磁法、地震、测井等地球物理方法为常用手段。基于地下水模型的地球反演地质解释优化方法大致实现过程为（图2）：

（1）采用合理的地球物理反演方法对野外实测数据进行反演成像；

（2）结合已知地质、钻探资料，对反演成像的结果做出合理的地质解释，由于反演的多解性，往往能得到多个解释结果；

（3）为了得到更合乎实际情况的地质解释，将（2）中所得的多个地质解释结果（包含岩性信息）转换成地下水模型（包含水力特性参数信息）；

（4）通过水文地质调查，确定边界定解条件、源汇项等相关水文信息，对（3）中地下水模型进行地下水数值模拟，得到不同地质解释结果对应地下水模型的水位、浓度信息；

（5）将（4）中模拟的水位、浓度信息与水文地质中水位、水质监测结果进行对比，最终确定更符合野外实际情况的地质解释。

本文从已知理想地质体出发，以大地电磁法为实现手段，通过数值模拟实现上述优化方法。已知水位、浓度的获取为已知理想地质体地下水数值模拟的结果。首先，采用MTsoft2D软件完成地球物理正演，得到反演数据输入并进行地球物理反演，反演过程中主要采用不同模式的选择、道间距以及插值频点的改变得到反演结果，进一步将其进行地质解释得到基于反演解释的地质模型。其次，将多个基于反演解释的地质模型转换成地下水模型，通过地下水数值模拟得到地下水模型的模拟水位、浓度分布。最后，统计多个基于反演解释的地质模型对应的模拟水位、浓度与已知理想地质体数值模拟的水位、浓度的标准偏差、均方根误差、归一化误差、平均归一化均方根误差、相关系数的大小，并比较各项误差大小，最终确定相对最佳地质模型，达到优化地球物理反演解释的目的。

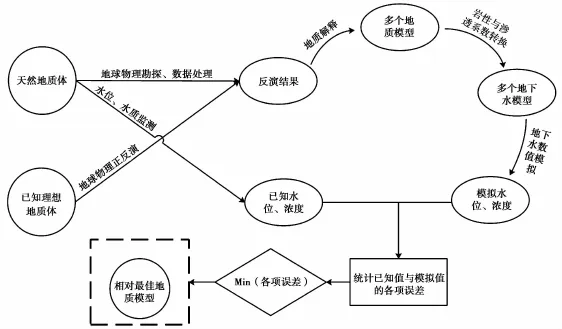
图2 基于地下水模型的地球物理反演解释优化方法实现图Fig.2 The chart of an optimization method for interpreting ERT data based on groundwater numericalmodeling

2 已知理想地质模型的建立

针对1.3节所述的基于地下水模型的地球反演解释优化方法，采用MTsoft2D建立给定地质模型Model i（图3）。模型长2000m，深300m，表层为25m厚的黏土覆盖层，中间为充填中砂的U型谷，U型谷中间为一条厚度为50m的黏土层，基岩为花岗岩。参照几种岩石电阻率值的分布范围曲线（李金铭，2005），取黏土电阻率为10Ω·m，砂岩为500Ω·m，花岗岩为10000Ω·m，得到构造地电模型。

3 大地电磁的正反演计算及反演解释优化方法

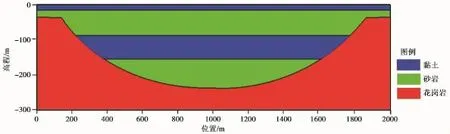
图3 已知理想地质模型Model iFig.3 The known geologicalmodel Model i

以上述已知理想地质模型为例，通过大地电磁法对其进行研究。电磁法常用的正演模拟软件有MTsoft2D，反演软件有MTsoft2D、SCS2D、GME_3DI（V4.1）等，本次MT正演模拟采用成都理工大学开发的MTsoft2D，数值解法为有限单元法。反演计算采用中南大学自主开发的重磁电三维反演成像解释一体化系统GME_3DI（V4.1），反演成像方法为二维连续介质广义逆快速反演（戴世坤等，1997）。

3.1 大地电磁正演计算

通过设置不同的网格剖分方式，根据模拟敏感性分析结果，采用垂直、水平剖线0.05、0.01km／格，并添加自动边界剖线最合适。水平方向共布置了41个测点，间距50m，频率为1.1250～7680.589Hz（共40个频点）。

图4分别为TE、TM模式正演模拟结果。从TE模式结果看（图4a），整个剖面的电阻率值在0～5000Ω·m之间，与模型所设计的电阻率相比有一定的差异，最高电阻率没有达到预期值10000Ω·m。从整个剖面上来看它分为3层，整体电阻率为低－中－高的趋势，并且能够看到U型谷的存在，但是并不能刻画U型谷中间低阻层的存在。而TM模式正演结果剖面（图4b）与TE模式相比整体趋势两者结果相似，但是基底的电阻率远高于TE模式，U型谷刻画得比较明显。

3.2 大地电磁反演

不同模式测量、插值频点数目以及道间距可以获得不同的反演结果，本文中采用不同模式测量、插值的道间距以及频点数描述反演解释多解性问题，并非描述地球物理反演算法的优劣。本次反演中采用了3种极化模式（TE、TM、TEM）以及3组插值后频率和间距（40，25）、（40，50）、（50，25）（原本频组为40频点，间距50m），反演深度300m，得到9个二维反演结果（图5）。

图5的Model 1-3、4-6、7-9分别为TE、TM、TEM模式频间组合为（40，25）、（40，50）、（50，25）的反演结果。从图5可知TE模式下不同参数反演断面图Model 1-3均能大致刻画U型谷中低阻带的存在，但详尽不一，3个反演结果与已知理想地质模型相比，存在低阻带与基岩不完全相连。Model 1刻画较完整，Model 2在低阻带的上部出现了带状高阻，Model 3的低阻带主要分布在U型谷的右半部分。TM模式Model 4、Model 5 U型谷中低阻隐约能显示，但Model 4顶部的低阻覆盖层和基岩部分已经不完整，尤其是Model 6、Model 9中间的低阻带已经缺失，失去原本模型的大致结构。TEM模式中的低阻带的Model 7、Model 8低阻也与基岩部分不相连，结果和Model 3相似。

3.3 大地电磁反演结果解释－地质模型

图6是基于大地电磁反演结果解释所得的地质模型，主要依据电阻率（李金铭，2005）的分区划分。由于黏土电阻率一般比较低，当电阻率低于50Ω·m划分为黏土。砂岩的电阻率变化范围比较大，50～1000Ω·m划分为砂岩。当电阻率大于1000Ω·m划分为花岗岩。

3.4 基于地下水数值模拟的优化方法

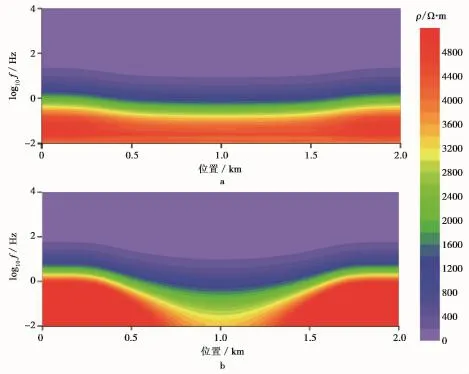
图4 TE模式（a）和TM模式（b）正演结果Fig.4 The results of TE（left）and TM（right）mode forward modeling

由上文可知，通过改变地球物理反演参数（插值的频点数、道间距）或者采用TE、TM、TEM不同测量模式，可以得到多个可供解释的大地电磁反演结果，但是具体哪个反演结果更符合已知理想地质模型，野外实测数据的反演到底哪一个更吻合地质解释，这就需要通过地下水模型来进行下一步的研究。

图5 大地电磁反演结果Fig.5 The results of MT inversion

3.4.1 地下水数值模型建立

本次数值模型的建立采用数值模拟软件Visual MODFLOW 2011.1，该软件由于其优良的可视化界面以及丰富的功能被广泛用于地下水数值模拟研究中（魏亚强等，2015；郑灿政等，2015），它集成了MODFLOW，MODPATH，MT3DMS、ZoneBudget、PEST模块，模块间相互独立，是三维地下水流动和污染物运移模拟实际应用中功能最为完整、操作比较简单、图形界面直观的专业软件。

地下水数值模型的建立主要包括以下几个步骤：

（1）空间剖分：研究模型长2000m，宽300m，剖面面积为2000×300m2，采用有限差分的方法进行矩形剖分，单元长10m，宽5m，共剖分了1行200列60层，单元总数12000个。

（2）边界、定解条件处理：所有地下水模型底部处理为隔水边界，左右边界设置为距离顶板厚度为10m定水头，水位分别为290m、315m，其他单元格的初始水位为290m。

（3）水文地质参数处理：参照不同岩性渗透系数经验值（中国地质调查局，2012），将不同岩性的区域赋相应的值，黏土、中砂、花岗岩依次为2.9e－6m·d－1、1.2e－4m·d－1、5e－13m·d－1，其他地质参数均采用系统默认值。

（4）源汇项来源：定水头边界的补给；降雨入渗（100mm·y－1）；在X方向500m，Z方向230～250m处设置注水井（注水量150m3·d－1），X方向1500m，Z方向90～110m处设置抽水井（抽水量200m3·d－1），每口注水井加入2个点污染源，浓度分别为400mg·L－1、500mg·L－1。

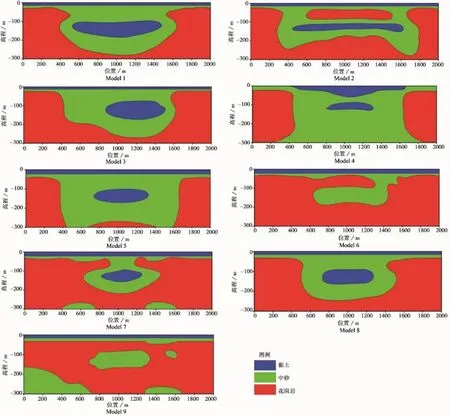
图6 基于大地电磁反演的地质解释Fig.6 The geological interpretation of MTmethod inversion

3.4.2 地下水流和溶质运移模拟结果

地下水流、溶质运移模拟分别使用的是Visual MODFLOW2011.1中MODFLOW、MT3DMS程序包。模拟非稳定流水位、浓度变化情况，时间为2000d。

在整个剖面上设立22口监测井监测激励源产生的响应。将已知理想地质模型对应的地下水流监测井的水位、浓度作为实测水位、浓度（Observation），地球物理解释对应的地下水模型的模拟水位、浓度作为计算水位、浓度（Calculation），统计观测值与计算值之间的各项误差，分别见表1、2。其中平均归一化均方根误差为归一化均方根误差与参与模拟计算模型归一化均方根误差平均值的比值，当模型间的差值大于5％，模型间具有很好的区分度。

从表1可知Model 4、Model 6、Model 7、Model 9的各项误差相比于其他模型均比较大，平均归一化均方根误差依次为169.7％、184.8％、163.1％、110.7％，远远高于平均值，根据相关系数的值可知这几个模型与实测值的相关性均比较低。Model 1、Model 3的各项误差都比较小，平均归一化均方根误差分别为43.7％、48.6％，但是平均归一化均方根误差差值小于5％，因此Model，1、Model，3并不具有很好的区分度。Model，2、Model，5的各项误差相当接近且Model，8的结果优于Model，2、Model，5。根据表1初步确定与Model，i的拟合优劣顺序为Model，1（3）、8、2（5）、9、7、4、6。

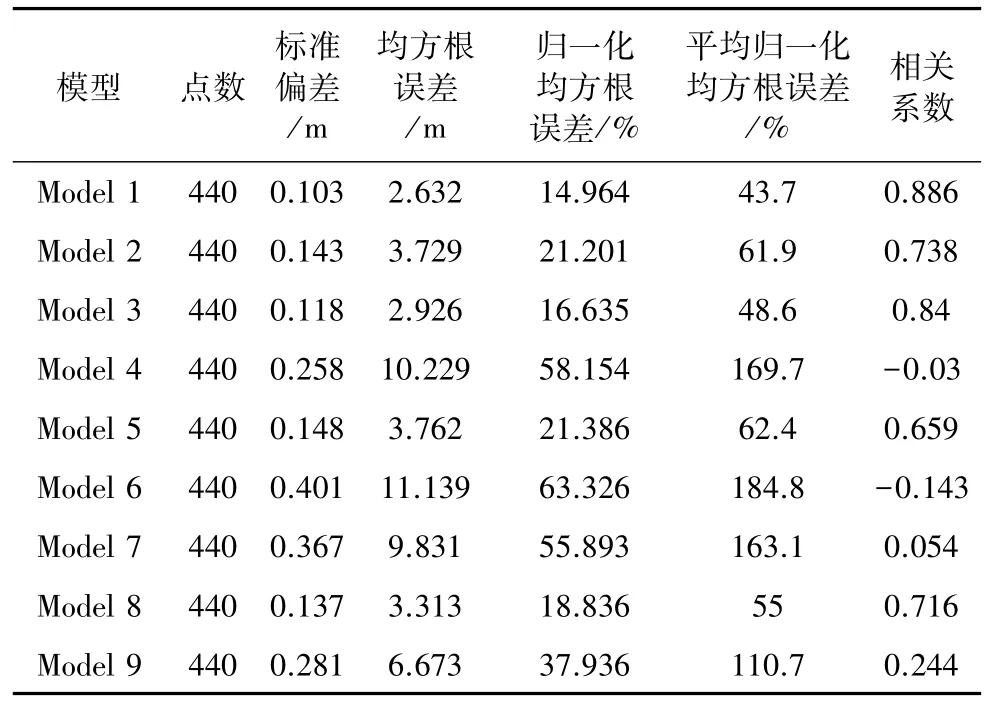
表1 不同地下水模型模拟水位与实测水位误差统计Table 1 The errors between observation and calculation water level ofmultiple geologicalmodels

从表2中可知Model 6、7、9的平均归一化均方根误差为131.2％，与已知理想地质模型的相关系数值接近于0。Model 3、5、8的误差的统计结果也相当接近，平均归一化均方根误差分别为79.5％、79.5％、77.8％（误差差值小于5％），在溶质运移中并不具有很好的区分度，Model 4各项误差远大于3、5、8。Model 1各项误差均为最小，与实测浓度拟合的最佳，与其他模型的平均归一化均方根误差最小差值也为16.2％。根据表2确定与Model i的拟合优劣顺序为Model 1、3（5、8）、2、4、6（7、9）。

从不同模型模拟水位、浓度与实测结果相比可知，不管是水流模拟还是溶质运移的结果，Model 6、7、9均被证明与已知理想地质模型差异性比较大，相关性几乎为0。Model 4在溶质运移中误差值也明显高于Model 1、3、5、8，在模拟水位误差中更容易体现。Model 1与2、3、5虽然在模拟水位上的各项误差值极为接近，但是在溶质运移中具有明显的区分度，类似有Model 3、5、8在溶质运移的结果相似，但是在模拟水位上存在明显的差异。以水流模拟为基础，当模型间的平均归一化均方根误差差值低于5％时，进一步利用溶质运移结果，从而得出与已知理想地质模型的拟合优劣顺序为：Model 1、3、8、5、4、9、7、6。

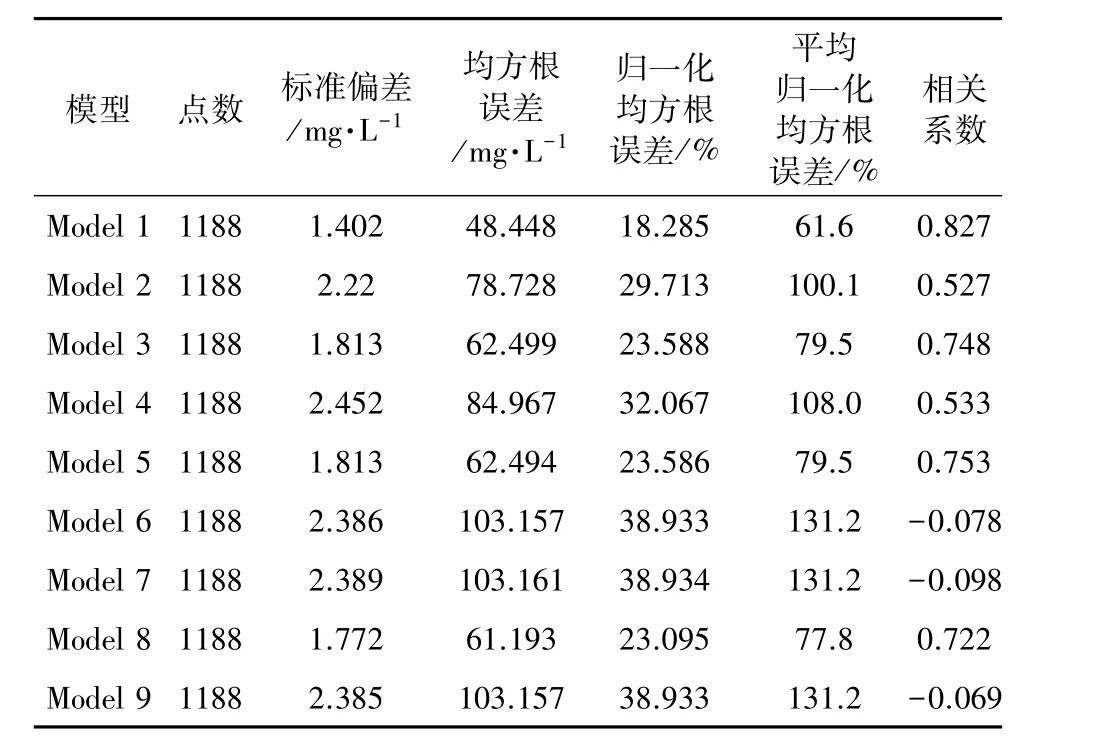
表2 不同地下水模型浓度观测值与计算值误差统计Table 2 The errors between observation and calculation concentration ofmultiple geologicalmodels

3.4.3 数值模拟中抽注水井灵敏度分析

由于3.4.2只分析一种抽注水情景，如何确定所得最佳拟合结果是偶然因素造成还是实际上就存在这么一种响应？本节主要来探讨这个问题。对于上述问题的研究，通过抽取上一小节中的4个地下水模型Model 1、3、5、8，敏感性分析通过更换抽注水井的位置来实现（其他条件保持一致），分别设置以下两种情景：

（1）情景一：X方向650m，Z方向80～100m处设置注水井（注水量150m3·d－1），X方向1500m，Z方向230～250m处设置抽水井（抽水量200m3·d－1）。

（2）情景二：X方向500m，Z方向230～250m处设置注水井（注水量150m3·d－1），X方向1000m，Z方向90～110m处设置抽水井（抽水量300m3·d－1），X方向1500m，Z方向230～250m处设置注水井（注水量100m3·d－1）。

类似于3.4.2，统计了情景一、二下不同地下水模型模拟水位（浓度）与实测水位（浓度）值误差（表3、表4）。

从表3中可知模型间平均归一化均方根误差差值均大于5％，因此Model 1、3、5、8具有很好的区分度，并不需要再运用地下水中的溶质运移模拟即可确定与已知理想地质模型拟合优劣顺序为Model 1、3、8、5。

从表4可以看出Model 1的各项误差均为最小，Model 5为最大，Model 1与Model 8两者平均归一化均方根误差差值8.5％，具有很好的区分度。而Model 3、8的平均归一化均方根误差差值2.3％，因此进一步对其进行溶质运移模拟，在浓度各项误差统计结果中模型间平均归一化均方根误差相差23.2％，所以通过溶质运移能够很好地将两者区分出来。在情景二下得到拟合顺序仍为Model 1、3、8、5。

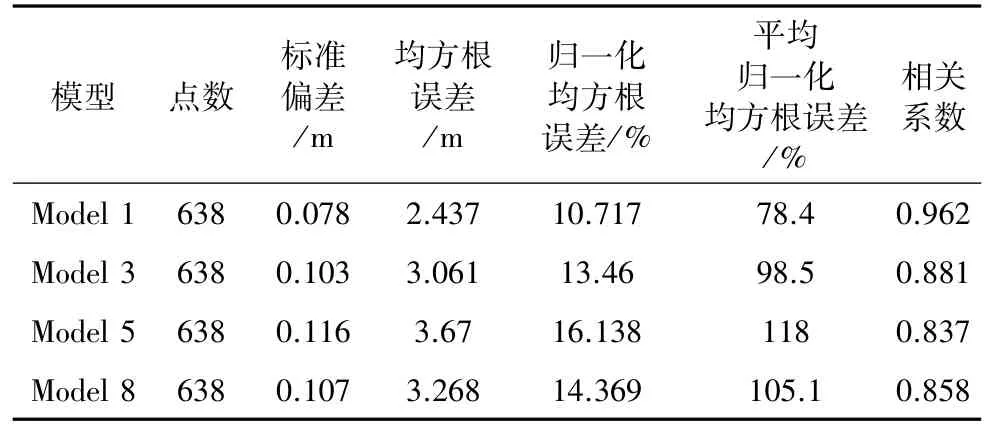
表3 情景一：不同地下水模型模拟水位与实测水位值误差统计Table 3 The scenario one：the errors between observation and calculation water level ofmultiple geologicalmodels

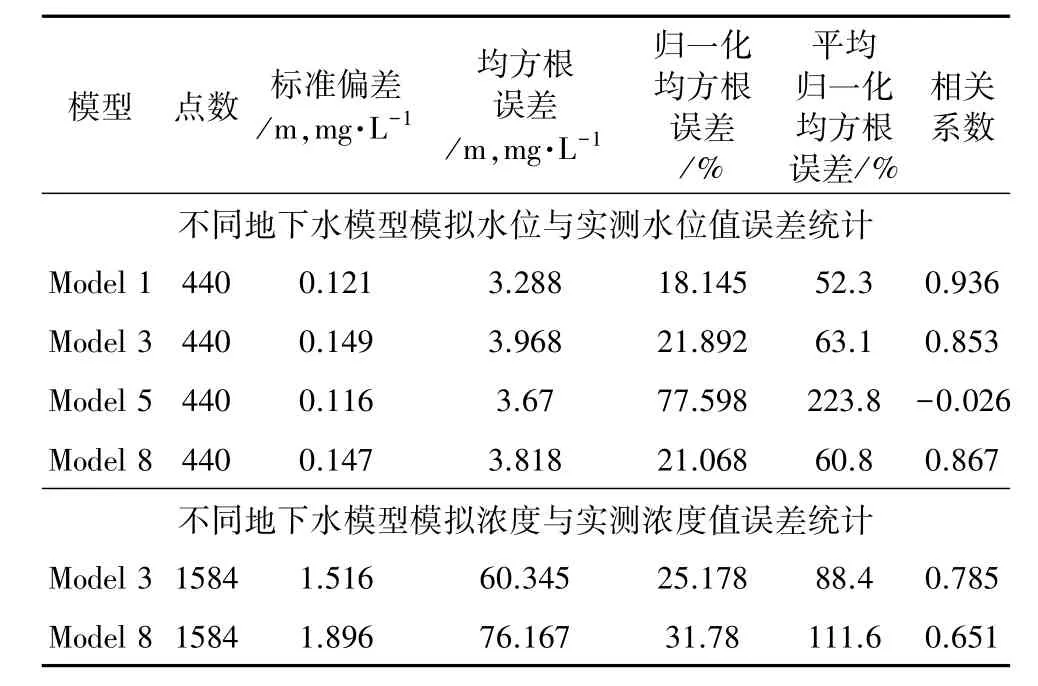
表4 情景二：不同地下水模型模拟水位与实测水位值误差统计Table 4 The scenario two

4 模拟结果与分析

通过大地电磁反演得到多个反演结果（图5），将其解释为地质模型（图6）并转换成地下水数值模型。当运用水位进行比较时，若存在两个、甚至多个模型不具有良好区分度、可以通过溶质运移进行进一步分析，最终确定与已知理想地质模型的拟合顺序，从而筛选出相对最优结果。

从模拟结果可知Model 2、4、6、7在地下水模拟中与Model i相差比较大，通过水位能很好地将其区分；对比地质模型Model 2、4、6、7与Model i的差异，从图6也能看出这4个模型确实与Model i的相似性比较差。对于Model 1、3、5、8尽管从地质模型的视觉效果上看，差异性可能并不是很大，但是通过地下水数值模拟可以很好地将其区分出来，并确定了Model 1为相对最佳地质模型。

从地下水数值模拟结果可知不管抽注水井的位置如何变化，均能确定与已知理想地质模型吻合最好的模型为Model 1，达到了优化反演地质解释结果的目的。

5 结论与展望

本文通过学科交叉与融合，针对地球物理反演结果解释的不确定性，探索了一种结合地下水模拟来优化地球物理反演解释思路。对于钻探和地质资料缺乏但具有较多可监测的地下水井孔的地区，该方法可为地球物理反演结果解释进一步限定，提供一种新的思路和方法。主要得到以下两点结论：

（1）提出了一种基于地下水模型的地球物理反演地质解释优化方法。

首先，地球物理勘探数据的前期处理，并采用合理的地球物理反演方法对数据进行反演成像。其次，结合已知地质、钻探资料，对反演成像的结果做出合理的地质解释；为了得到更合乎实际情况的地质解释，将反演成像所得的多个地质解释结果转换成地下水模型，通过水文地质调查，确定边界定解条件、源汇项等相关水文信息，对地下水模型进行地下水数值模拟，得到基于不同地质解释结果对应地下水模型的模拟水位、浓度信息。最后，将模拟水位、浓度信息与水文地质中水位、水质监测结果进行对比，从而确定更符合野外实际情况的地质解释。

（2）通过地下水流、溶质运移模拟结合的方式证明了方法的可行性。

文中以已知理想地质模型和大地电磁法为例。首先，建立已知理想地质模型，并对给定地质模型进行大地电磁正反演、得到多个基于大地电磁反演解释的地质模型。为了进一步优化反演解释结果，将已知理想地质模型以及基于反演解释的地质模型进行水流和溶质运移模拟，统计各项误差，最终确定了相对最佳地质模型。通过敏感性分析，不管抽注水井位置如何，均得到相同的结果，达到了优化反演解释的目的，很好地验证了运用地下水流、溶质运移数值模拟搜索相对最佳地质模型的可行性。

本研究中反演结果解释部分仍然存在一定的主观性、局限性，在未来研究中需要做进一步的完善，如通过大量的数值模拟实验、实验室测量建立电阻率与渗透系数的映射关系，或者将地下水约束加入地球物理反演算法中，从算法上优化反演结果。

Andersen T R，Poulsen SE，Christensen S，et al.2013.A synthetic study of geophysics-based modelling of groundwater flow in catchments with a buried valley［J］.Hydrogeology Journal，21（2）：491～503.

Chen C X，Lin M.2009.Groundwater Hydraulics［M］.Wuhan：China University of Geosciences Press：1～300.

China Geological Survey.2012.Hydrogeological manual［M］.Beijing：Geological Publishing House：1－874.

Chen J，Wen N，Chen B Y.2007.Joint inversion of gravity-magneticelectrical－seismic combination survey：progress and prospect［J］. Progress in Geophysics，22（5）：1427～1438.

Chen S Y.2014.Research and application of integrated geophysical interpretation method［D］.Chengdu：Chengdu University of Technology.

Dai QW，Chen D P，Chen Y X，etal.2013.The enhanced algorithmsand its implementation for the abnormal response characteristics in electrical exploration［J］.Coal Geology＆Exploration，41（3）：75～78.

Dai SK，Xu S Z.1997.Rapid inversion ofmagnetotelluric data for 2-D and 3-D continuousmedia［J］.Oil Geophysical Prospecting，32（3）：305～317.

Guo D，Yan JY，Lu Q T，et al.2014.3D Densitymapping constrained by geological information：model study and application［J］.Acta Geologica Sinica，88（4）：763～776.

He W H，Wang JL，Yu P.2009.Overview of the status and prospect of geophysical joint inversion［J］.Progress in Geophysics，24（2）：530～540.

Jing R Z，Bao G S，Chen S Q.2003.A review of the researches for geophysical combinative inversion［J］.Progress in Geophysics，18（3）：535～540.

Li J M.2005.Electric field and electric prospecting［M］.Beijing：Geological Publishing House：1～473.

Ling D M，Sang Y J，Jin W J，et al.2014.Preliminary study of rockphysics and physical properties of rockmass structure［J］.Journal of Engineering Geology，22（6）：1154～1158.

Panday S，Langevin C D，Niswonger R G，et al.2013.MODFLOW-USG version 1：An unstructured grid version of MODFLOW for simulating groundwater flow and tightly coupled processes using a control volume finite-difference formulation［R］.Washington：US Geological Survey.

Qi G.2013.3D gravity and magnetic inversion modeling constrained by geological information［D］.Jilin：Jilin University.

Singha K，Gorelick S M.2006.Hydrogeophysical tracking of threedimensional tracer migration：The concept and application of apparent petrophysical relations［J］.Water Resources Research，42（6）：1～14.

Wang J Y.2002.Inverse theory in geophysics［M］.Beijing：Higher Education Press：1～187.

Wei C，Li X F，Zhang M G.2008.The geophysical inversemethod based on quantum Monte Carlo［J］.Chinese Journal of Geophysics Chinese，51（5）：1494～1502.

Wei Y Q，Qiao X J，Li G M.2015.Influence on calculation accuracy by differentalgorithms and parameters in MODFLOW［J］.Hydrogeology＆Engineering Geology，42（1）：14～21.

Wu G，Hu X Y，Huo G P，et al.2012.Geophysical exploration for geothermal resources：An application of MT and CSAMT in Jiangxia，Wuhan，China［J］.Journal of Earth Science，23（5）：757～767.

Xu S Z.1994.Finite element method in Geophysics［M］.Beijing：Science Press：1～308.

Xue Y Q，Xie C H.2007.Numerical simulation of groundwater［M］. Beijing：Science Press：1～451.

Yang W C.2002.A perspective to development of geophysical inversions［J］.Earth Science Frontiers，9（4）：389～396.

Yeh T C J，Liu S，Glass R J，et al.2002.A geostatistically based inverse model for electrical resistivity surveys and its applications to vadose zone hydrology［J］.Water Resources Research，38（12）：14－1－14－13.

Yu P，Wang J L，Wu J S，et al.2006.Review and discussions on geophysical joint inversion.［J］.Progress in Exploration Geophysics，29（2）：87～93.

Yu Y X，Wu JC.2006.Application of electrical resistivity tomography data to estimate hydraulic conductivity in porous medium［J］. Hydrogeology＆Engineering Geology，33（2）：41～44，49.

Yuan SY，Wang SX，Tian N.2009.Swarm intelligence optimization and its application in geophysical data inversion［J］.Applied Geophysics，6（2）：166～174.

Zheng C X，Wang P P.1999.A modular three-dimensionalmulti-species transportmodel for simulation of advection，dispersion and chemical reactions of contaminants in groundwater systems；documentation and user's guide［R］.Vicksburg，Mississippi，USA：US Army Engineer Research and Development Center Contract Report SERDP-99－1.

Zheng C Z，Tong L Y，ZhangM F，etal.2015.Characteristics of effects on groundwater flow by underground structures［J］.Journal of Engineering Geology，23（S1）：553～557.

陈崇希，林敏.2009.地下水动力学［M］.武汉：中国地质大学出版社：1～300.

陈洁，温宁，陈邦彦.2007.重磁电震联合反演研究进展与展望［J］.地球物理学进展，22（5）：1427～1438.

陈思宇.2014.地质－综合地球物理联合解释方法研究及应用［D］.成都：成都理工大学.

戴前伟，陈德鹏，陈勇雄，等.2013.电法勘探中异常响应特征的增强算法及其实现［J］.煤田地质与勘探，41（3）：75～78.

戴世坤，徐世浙.1997.MT二维和三维连续介质快速反演［J］.石油地球物理勘探，32（3）：305～317.

郭冬，严加永，吕庆田，等.2014.地质信息约束下的三维密度填图技术研究及应用［J］.地质学报，88（4）：763～776.

何委徽，王家林，于鹏.2009.地球物理联合反演研究的现状与趋势分析［J］.地球物理学进展，24（2）：530～540.

敬荣中，鲍光淑，陈绍裘.2003.地球物理联合反演研究综述［J］.地球物理学进展，18（3）：535～540.

李金铭.2005.地电场与电法勘探［M］.北京：地质出版社：1～473.

林达明，尚彦军，金维浚，等.2014.岩石物性与岩体结构物性研究进展［J］.工程地质学报，22（6）：1154～1158.

祁光.2013.地质条件约束下重磁三维反演建模方法研究［D］.吉林：吉林大学.

王家映.2002.地球物理反演理论［M］.北京：高等教育出版社：1－187.

魏超，李小凡，张美根.2008.基于量子蒙特卡罗的地球物理反演方法［J］.地球物理学报，51（5）：1494～1502.

魏亚强，乔小娟，李国敏.2015.MODFLOW不同算法及参数设定对计算精度的影响［J］.水文地质工程地质，42（1）：14～21.

徐世浙.1994.地球物理中的有限单元法［M］.北京：科学出版社：1～308.

薛禹群，谢春红.2007.地下水数值模拟［M］.北京：科学出版社：1～451.

杨文采.2002.评地球物理反演的发展趋向［J］.地学前缘，9（4）：389～396.

于鹏，王家林，吴健生，等.2006.地球物理联合反演的研究现状和分析［J］.勘探地球物理进展，29（2）：87～93.

喻永祥，吴吉春.2006.利用ERT数据推求非均质多孔介质渗透系数初探［J］.水文地质工程地质，33（2）：41～44，49.

郑灿政，童立元，张明飞，等.2015.地下水结构对地下水流场影响的特性规律［J］.工程地质学报，23（S1）：553～557.

中国地质调查局.2012.水文地质手册［M］.北京：地质出版社：1～874.

AN OPTIM IZATION METHOD FOR INTERPRETING ERT DATA BASED ON GROUNDWATER NUMERICAL MODELING

LIXuelan①DONG Yanhui②LIDiquan①③
（①School of Geosciences and Info-Physics，Central South University，Changsha 410083）
（②Institute of Geology and Geophysics，Chinese Academy of Sciences，Beijing 100029）
（③Key Laboratory of Metallogenic Prediction of NonferrousMetals，Ministry of Education，Central South University，Changsha 410083）

Geophysical non-uniqueness are everywhere.Faced with this situation we usually tend to combine geological data to calibrate the interpretation results.However，the information on geology and deep drilling are deficiency in remote areas，and field existing wells are often difficult to obtain information on lithology catalog，which will cause that the inversion results are difficult to interpret.Whether hydraulic characteristics of the water level and water quality information contained in the geological body can be used to assist the geophysical inversion？Based on this idea，amethod for interpreting ERT data based on groundwater numericalmodeling is provided in this article.In this article，Magneto-telluric method is a way to accomplish numerical simulation of geophysical forward and inversion.Firstly，by studying the known geologicalmodel andmultiple geologicalmodels interpreted from ERTdata，a set of groundwater numericalmodels can be set up.Then numerical simulation of groundwater flow and solute transportwere conducted.Lastly，the optimal geologicalmodel can be obtained by comparing the result of numerical simulation of groundwater.Sensitivity analysiswere also conducted to verify themethod.

Geophysical inversion，Geologicalmodel，Numerical simulation of groundwater flow，Solute transport

P641.7

：A

10.13544／j.cnki.jeg.2016.06.037

2015－10－15；

2016－06－16.

国家自然科学基金（41202182）资助.

李学兰（1993－），女，硕士生，从事地球探测信息与技术研究.Email：lixuelan＠csu.edu.cn

董艳辉（1980－），男，博士，副研究员，主要从事水文地质方面研究.Email：lemondyh＠mail.iggcas.ac.cn