混沌实验分层教学探究

罗湘南， 唐建锋

(衡阳师范学院 物理与电子工程学院，湖南 衡阳 421002)

混沌实验分层教学探究

罗湘南， 唐建锋

(衡阳师范学院 物理与电子工程学院，湖南 衡阳 421002)

混沌实验是学生了解非线性科学的重要教学内容。在教学实践中，我们分三个层次循序渐进开展实验教学，即观察生活中的混沌现象、观察蔡氏电路混沌现象、初步探究蔡氏电路混沌现象产生的原因。实验教学收到了良好的效果，学生对混沌现象的特点、产生原因有了较深入的认识。

混沌现象；蔡氏电路；混沌吸引子；非线性负阻

1 引 言

混沌是在确定的非线性动力系统中出现的一种对初值敏感的貌似无规则、类似随机的现象，它是非线性动力系统所特有的复杂现象，在自然界和社会生活中普遍存在。现在，“混沌”是近代理论研究热点，已经形成了一门新的科学，它涉及的领域包括数学、物理学、生物学、化学、天文学、经济学及工程技术的众多学科，研究成果产生一些实用价值，并对这些学科的发展产生深远的影响。有预言，混沌理论将掀起继相对论和量子力学以来基础科学的第三次革命[1]。

在理工科教学中，紧跟现代科技前沿，适当增加非线性内容教学非常必要。为此，我校在近代物理实验中开设了《混沌实验》，开拓学生视野。学生长期学习牛顿经典理论，知道物体的初始状态和受力情况就可以预测物体未来的状态，这与混沌理论的运动状态不确定不可预测完全冲突，为了解决这种冲突，取得好的教学效果，我们通过三个层次进行教学，让学生对混沌现象、成因及特点逐步形成深刻的印象。

2 混沌现象的感性认识

事实上，混沌现象普遍存在我们的自然和社会生活。所以，在课堂教学前，我们先让学生观察生活中的混沌现象。例如，观察点燃的香烟，一缕缕青烟离开烟头几乎直线往空中升起，突然卷成扰动的一团烟雾，上下翻滚，然后四处飘散；观察平稳的水流突然四处飞溅等，通过仿真试验教学平台让学生观察三叉混沌摆的完全不同步随机的摆动视频等[2]，总结所观察的现象的特点。再让学生阅读有名的“蝴蝶效应”等资料，通过这些学习，大部分同学都能发现这些现象共同点是突然从有序变为无序，认识到牛顿力学的局限，形成混沌现象感性认识，初步了解混沌的基本特点。

3 蔡氏电路混沌现象观察

在实验课堂学习中，让学生观察蔡氏电路的混沌现象，蔡氏电路结构如图1。该电路能展示混沌产生的过程，混沌吸引子的动态也很明晰。有源非线性负阻元件Nr是采用两个运算放大器(一个双运放LF353)和六个配制电阻来实现，其电路如图2所示，双运算放大器中两个对称放大器各自的配置电阻相差100倍，这就使得两个放大器输出电流的总和，在不同的工作电压段，输出总电流随电压变化关系不相同(其中一个放大器达到电流饱和，另一个尚未饱和)，因而出现了非线性的伏安特性[3]。实验中我们主要观察信号振动周期产生分岔和混沌等一系列非线性现象，深入了解混沌现象的主要特点与混沌现象的产生途径。

图1 蔡氏电路

图2 非线性负电阻的内部结构

3.1 混沌产生途径观察。

混沌现象产生途径一般有倍周期分叉和阵发混沌。观察前，按图1和图2接好电路，示波器选择X -Y工作方式。调节G(R1+R2和组成，R1为粗调，R2为细调)，阻值从最大逐渐减小，观察李萨如图的变化，如将一个环相图周期定为一，随着G阻值的减少，相图变化过程为：不动点→一倍周期→二倍周期→四倍周期→阵发混沌→三倍周期→单吸引子→双吸引子→极限环→直线。相图变化过程见图3。在三倍周期处，仔细调节R2，原先的混沌吸引子突然出现了一个三周期图像，继续微调R2，又出现了混沌吸引子，这一现象称为出现了周期性窗口。实验过程我们看到，电路先产生丰富的倍周期分岔，在三倍周期处，出现周期性窗口进入混沌状态，倍周期分岔是非线性确定性系统通向混沌最典型的形式。

3.2 混沌现象的特性观察。

1.对初值的敏感依赖。混沌的典型特征之一是对初值非常敏感。若两次运动的初值有微小差别，长时间后两次运动会出现较大的、无法预知的偏差。

图3 通往混沌的相图顺序

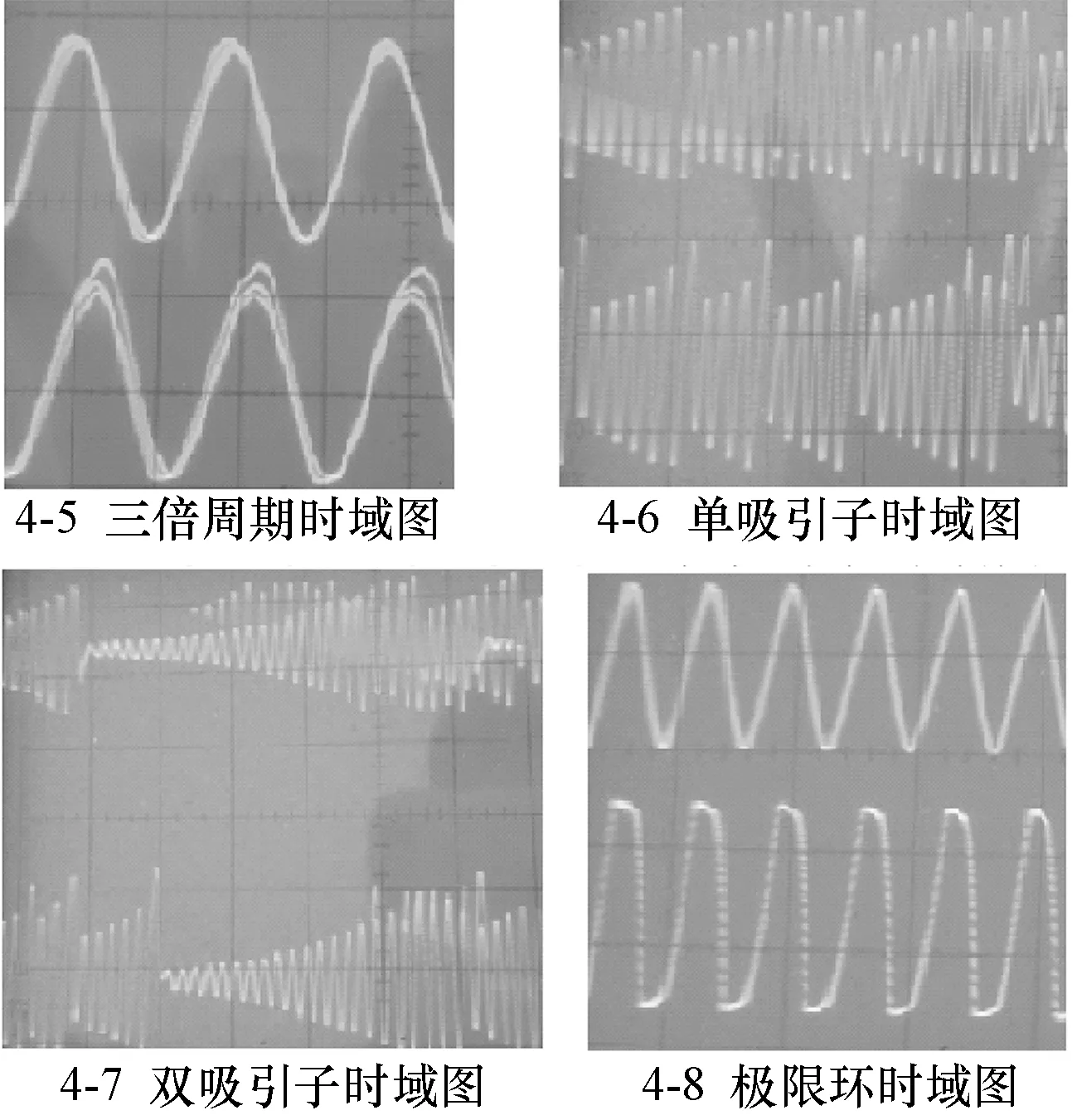
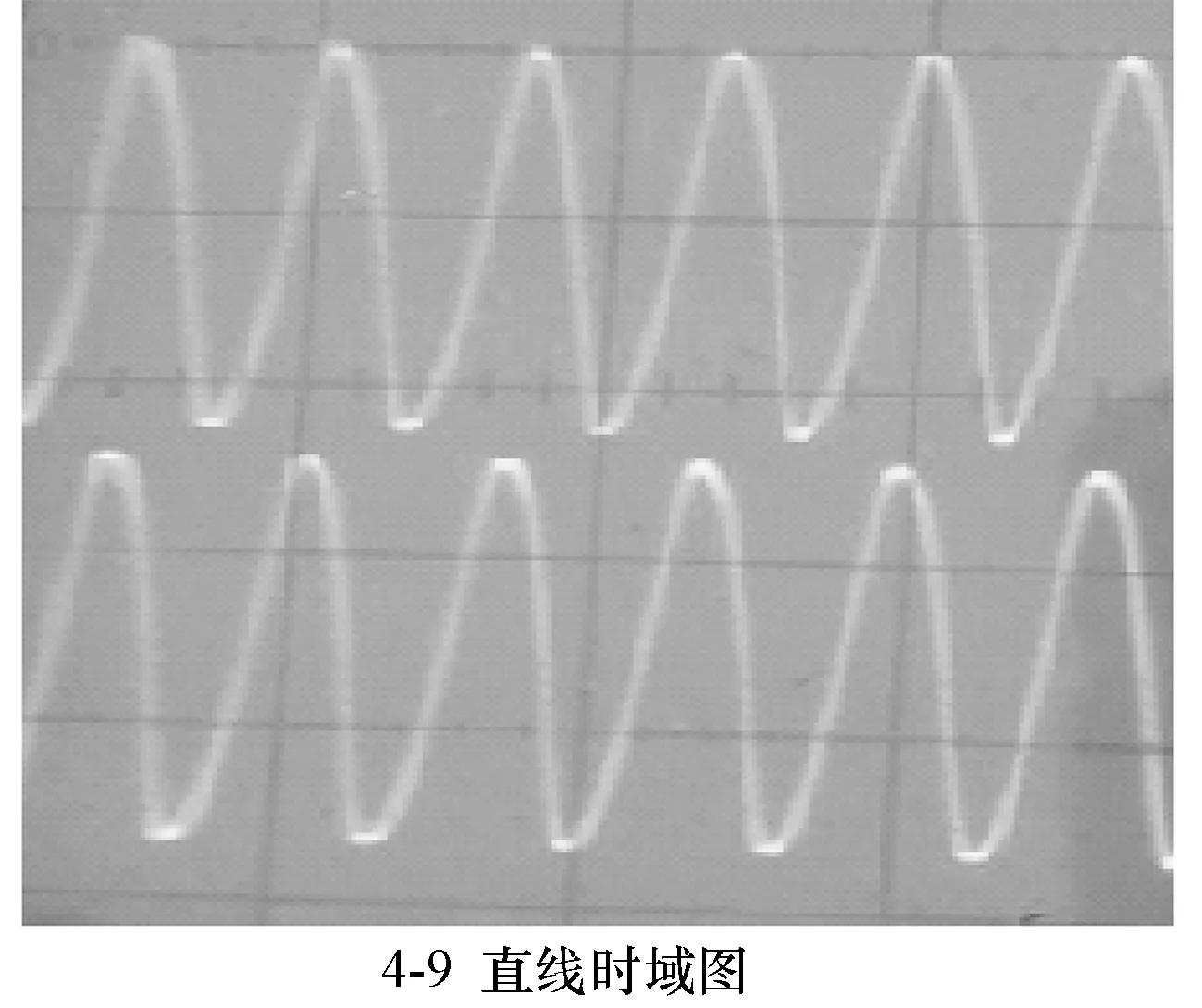
图4 通往混沌的时域图顺序

在上面的实验步骤中，当电阻调到某些临界状态时，如G=1 850时，微调R2，电路系统可出现阵发混沌，也可能出现三倍周期，还可能是单奇异子。另外如果在电路中加入万用表测G两端电压的有效期，屏幕的相图马上突变，有一倍周期突变为单吸引子，或双吸引子。这是由于万用表引入的电阻及电容效应，对电路产生细微的扰动，结果，因这些微小的差别造成实验结果的突变。

2.混沌信号的非周期性与分形。实验时，仔细观察图3的单吸引子、双吸引子，只见环状曲线在两个向外涡旋的吸引子之间似乎按照某种规律不断地填充与跳跃，可是在有限的空间里，跳动的曲线却不重复，也不会在吸引点附近交叉，总看不到曲线跳动填充运动的停止，一圈一圈填充的曲线形状很相似，相似的曲线填充运动永无休止，体现了混沌运动的非周期性以及分形特点。从填充运动的方向看，一切位于吸引子之外的曲线填充运动都在向吸引子靠拢，因而，曲线不停填充的空间不向外扩张，填充区域整体不变，呈现稳定的状态，而一切到达吸引子内部的曲线填充运动都相互排斥，不停地跳动，处于不稳定状态。吸引子这种非周期性与分形结构，体现了混沌不是绝对无序，而是呈现非周期有序性。

3.混沌信号具有内在的类噪声性。将示波器置于时域模式，重复上述步骤，各周期的CH1和CH2的时域信号如图4的9个分图所示。实验时，仔细观察比较，一倍周期信号的基本波形形状与周期加倍之后乃至混沌信号的基本波形形状相同，周期加倍主要引起波形包络线的变化，引起这些包络线变化的正是类似噪声的无规则振荡，但它不同于真正的噪声，仔细观察时域信号图，我们发现信号从点平衡态演变混沌信号的过程中，混沌信号中的这些类噪声的频率对平衡态信号频率还是有一定继承性。因而混沌中的这种类似噪声的信号不是真正的噪声，而是一种有内在规律的随机信号。

4 蔡氏电路混沌现象的产生原因

通过对蔡氏电路混沌现象的观察，学生对混沌的特性有了清晰地认识，但对所观察到的混沌现象演变原理，非线性动力系统的作用机制，没有实践体验。在蔡氏电路中唯一非线性元件为负阻，为了弄清非线性负阻对蔡氏电路产生混沌现象的作用，我们先测量负阻的伏安特性，再同步观察蔡氏电路信号不同相图下负阻的伏安特性，来探究混沌现象演变与非线性动力的关系。

测量伏安特性曲线的电路如图5[4]所示:把非线性负阻Nr与一个1千欧姆定值电阻R串联后用信号发生器输出的正弦波作电源驱动，用数字示波器观察定值电阻R两端的电压和Nr两端电压构成的李萨如图形，即可得到Nr的I-U特性。我们在500 Hz频率的正弦波信号扫描下，得到的I-U特性曲线如图6所示，以后频率增加至2 700 Hz时(发生混沌时的主频率附近)，I-U特性曲线形状不变。然后按图7所示用示波器观察C1与C2处信号构成的相图，用交流数字电压表和电流表观察非线性负阻的电压和电流。调节G逐渐减少，观察到的各种混沌现象与非线性负阻的电压与电流情况见表1。

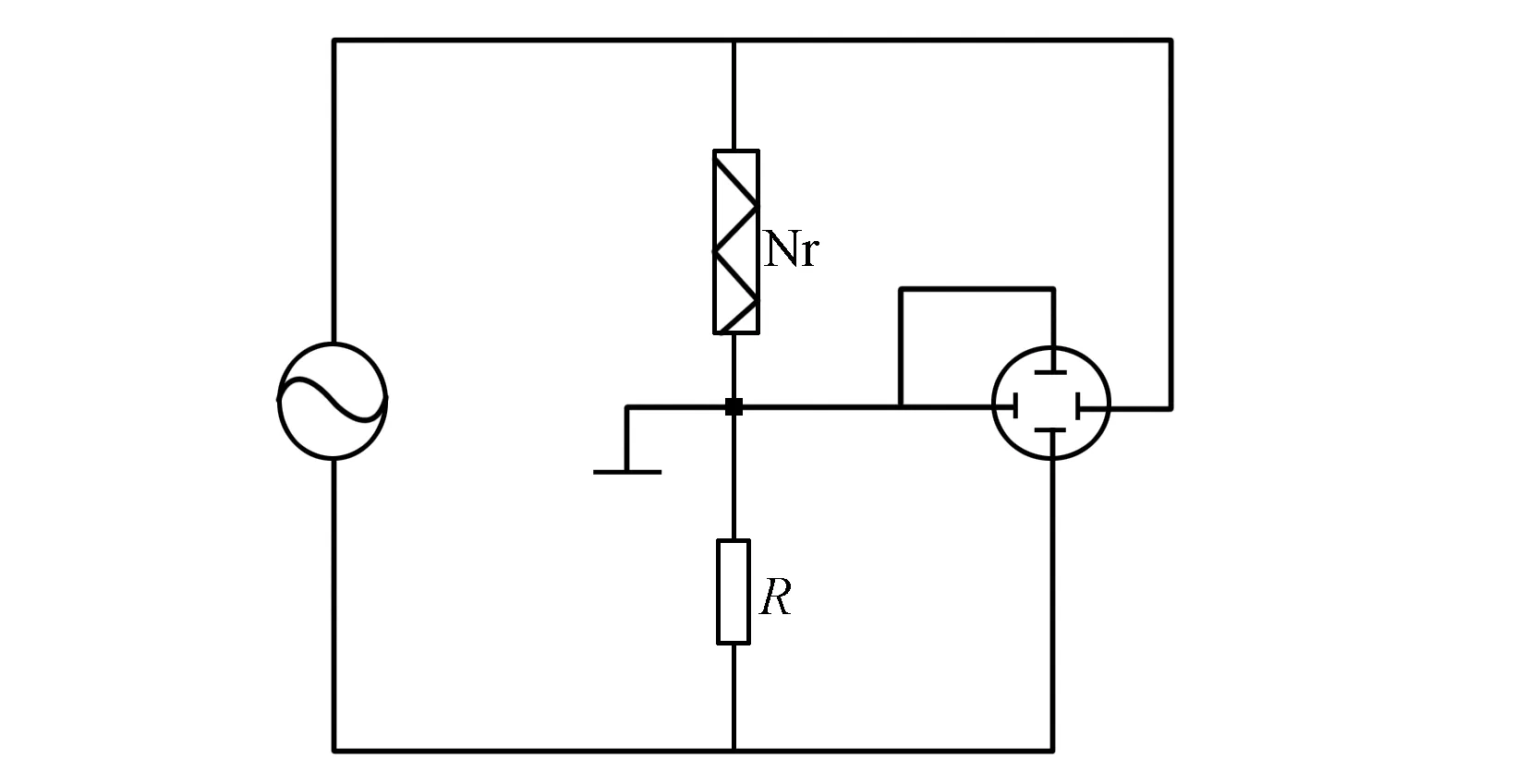
图5 测Nr伏安特性电路

图6 Nr伏安特性曲线

图7 相同与Nr的U-I观察电路

相图Nr的电压与电流的变化范围在图6伏安特性的位置不动点(-11.98V,5.2mA)到(-7.64V,3.63mA)之间。每个G,对应一组稳定的(V,mA)大约位于BC段上面部分一倍周期(-7.72V,3.73mA)到(-6.65V,3.27mA)之间。每个G,对应一组稳定的(V,mA)大约位于BC段中间部分二倍周期(-6.618V,3.27mA)到(-6.59V,3.26mA)之间。每个G,对应一组稳定的(V,mA)大约位于BC段中间部分四倍周期(-6.45V,3.20mA)到(-6.34V,3.17mA)之间。每个G,对应一组稳定的(V,mA),相图能处于四倍周期,G的变化范围很窄。大约位于BC段下面部分,阵发混沌(-6.37V,3.18mA)到(-6.17V,3.09mA)之间。每个G,对应一组稳定的(V,mA)。相图能处阵发混沌态时,G的变化范围很窄。大约位于BC段接近O点处小部分

续表

相图Nr的电压与电流的变化范围在图6伏安特性的位置单吸引子(-6V,2.99mA)到(-1.64V,-0.23mA)之间。G不变,电表的数值变动,不稳定。大约位于BCOD段双吸引子(-6V,3.22mA)到(5.8V,-2.5mA)之间,G不变,电表的数值快速变动,不稳定。大约位于BCODE段

实验中，没有观察三倍周期相图。数据表明四倍周期和阵发混沌的伏安区有重叠，此处在前期试验中观察到周期窗口，说明此处进入产生混沌的临界状态。由上表的数据可知: 非线性负阻的I-U工作在不同的区段，电路的相图呈现不同的状态，当蔡氏电路出现单吸引子混沌现象时，Nr的伏安曲线处于图6中B、C、O、D段或处于C、O、D、E段，当蔡氏电路出现双吸引子混沌现象时，Nr的伏安曲线处于图6中B、C、O、D、E段。实验表明，当Nr工作在整个伏安区即呈现非线性特性时，电路信号进入混沌状态。因而非线性负阻在蔡氏电路产生混沌过程中起的决定性作用，非线性动力是混沌现象产生的根本原因。

5 总 结

通过分层教学法学习混沌实验，学生突破了以前学习经典理论时所形成的传统认知，对无序混乱不确定混沌现象及产生的机制——非线性动力，有了较深入的认识,整个实验教学效果良好。

[1] 蒋达娅,肖井华,朱洪波,等.大学物理实验教程[ M].2版.北京:北京邮电大学出版社,2007.

[2] 张连芳,傅敏学,刘滢滢，等. 混沌实验教学之路[J]. 物理与工程，2013，23(1)：21-24.

[3] 王殿学.蔡氏电路中混沌现象与非线性电阻伏安曲线关系的研究[J]. 辽东学院学报(自然科学版),2010,17(4)：318-320.

[4] 罗页,乐永康.蔡氏非线性电路的深入研究——参数测量和实验现象观察的新方法[J]. 大学物理, 2010,29(6)：53-57.

(编校 高 峰 实习生 郭齐旗)

Research the Way of Layered Education for Chaos Experiments

LUOXiang-nan,TANGJian-feng

(College of Physics and Electronic Engineering,Hengyang Normal University,Hengyang Hunan 421002,China)

Chaos experiment is an important teaching content for students to understand the Nonlinear science.In teaching practice,we have teached student three levls step by step.they are Observeing Chaos in life,Observeing Chaotic phenomena of Chua's circuit and Researching the root cause of Chaotic phenomena.Experimental teaching has received good effect,student can have a deep understanding of characteristics of phenomena and the nonlinear driving force of Chaotic phenomena in the Chua's circuit.

Chaotic phenomena; Chua's circuit; chaos attractor; nonlinear resistance

2016-10-08

衡阳师范学院教学改革研究项目(JYKT201431)；光电信息省级平台开放项目(GD14K11)；光学—湖南省重点建设学科，电子信息类专业校企合作创新创业教育基地

罗湘南(1970-)，女，湖南衡阳，高级实验师，硕士，从事大学物理实验教学与研究。

O0413.1

A

1673-0313(2016)06-0080-04