新课标下中职数学情境教学研究

葛云虎

新课标下中职数学情境教学研究

葛云虎

《数学课程标准》要求教师创设适当的教学情境，让学生主动地学习，自主发现数学的规律和问题解决的途径，使学生经历知识形成的过程。教师应创设能够激发学生学习兴趣、使其乐于探索的学习情境，充分调动学生学习、探索的积极性、主动性，从而最大程度地提高学习效率。

中职；数学教学；新课程理念；情境教学；新课标

教育家第斯多惠说过：“教育艺术不在于传播的本领，而在于激励、唤醒和鼓舞学生的一种教学艺术。”创设具体、生动的课堂教学情境，正是激励、唤醒和鼓舞学生的一种教学艺术。[1]德国一位学者有过一句精辟的比喻：将15克盐放在你的面前，无论如何你都难以下咽；但当将15克盐放入一碗美味可口的汤中，你早就在享用佳肴时将15克盐全部吸收了。情境之于知识，犹如汤之于盐，盐需溶入汤中，才能被吸收；知识需要溶入情境之中，才能显示出活力和美感。教师可以创设适当的问题情境，以便于展开探究、讨论、理解等教学活动，促使学生在教学情境中进行探索，达到解决问题的目的，从而提高课堂教学效果。

一、利用数学与实际生活的联系创设情境

数学来源于实际生活，又在工农业生产和日常生活中都有广泛的应用，新教材一个明显的特点就是每章都出现了不少与本章内容有关的实例。[2]因此，在教学中要注重教学内容的现实性和应用性，要对教材进行必要的调整和加工，选择与学生现实生活中密切相关的情境和问题，选用学生喜闻乐见的材料，把生活中的鲜活题材引入课堂教学，赋予现行教材内容以新的活力，让学生感受到数学就在现实生活，燃起学生学习热情。

案例1：在中等职业学校数学教材第二册第24页例3：某人购买一辆20万元的车,首付5万元,其余车款按月分期付款,10年付清。如果欠款按月利率为0.5%计算，并把利息平均加到每月还款额上，那么此人每月应付款多少元?(精确到1元)

分析：汽车总价为20万元，首付5万,贷款15万元。

10年内每月应付欠款150 000/10×12=1 250(元)。

第一个月利息为150 000×0.5%=750(元);

第二个月利息为(150 000-1 250)×0.5%= 743.75;第三个月利息为(150 000-2×1 250)× 0.5%=737.5;

……

由此可知,10年中每月所付利息是以750为首项,-6.25为公差的等差数列{an},直到an=0为止。

由an=750+(n-1)×(-6.25)=0,

解得：n=121

所以总计利息是{an}的前121项之和S121

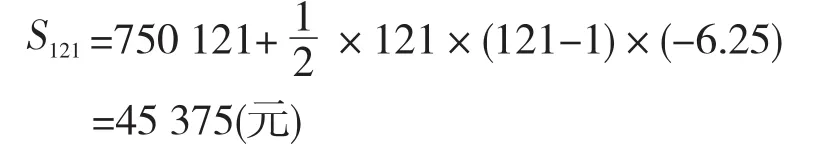
现把利息平均加到每月还款额上,所以每月还款额为1 250+45 375/10×12≈1 628(元)。

上例是利用数列解决（汽车贷款）分期付款中的实际应用。“分期付款”是数列的重要应用。分期付款汽车问题，银行称为商业性个人汽车贷款。在验证了相关证件后，即可签订个人商业汽车借款申请表，办理相关手续。分期付款不是贷款越多越好，也不是贷款期限越长越好。贷款与存款是两码子事，通过计算应该明白：若有富余的钱，还是小额贷款，贷短期款，有还款能力，有收益更高的投资，再谨慎贷款；贷款后按约还款，尽早还款，这才是在分期付款中最理智的选择。

案例2：在等比数列的前n项和公式的教学中，一位教师在讲授《等比数列的前n项和公式》时，对学生说：同学们，我愿意在一个月（按30天算）内每天给你们1 000元，但在这个月内，你们必须：第一天给我返回1分钱，第二天给我返回2分钱，第三天给我返回4分钱，即后一天返回的钱数是前一天的2倍，你们愿不愿意？此问题一出立即引起学生的极大兴趣，这么“诱人”的条件到底有没有陷阱？只有算出“收支”对比，才能回答愿与不愿。“支”就是一个等比数列的前n项和的问题，如何求出这个等比数列的前n项和呢？这就需要探索出等比数列的求和方法及求和公式。通过这个例子，不但使学生产生求知的热情及浓厚的兴趣，而且对引出等比数列的前n项和公式起到自然引入的作用。

案例3：在两个平面垂直的判定定理的教学中，老师提出：建造一座大楼，怎样才能使墙面与地面垂直呢？学生很快会联想到建筑工人常常用一端系着铅锤的细绳让其垂直地面，并以这根绳子为参照，看看所砌的墙是否经过这条细绳。然后问：为什么若墙面经过这条绳子，所砌的墙就与地面垂直呢？还可以引导学生观察教室门板与地面的位置关系，它们是否垂直？转动门扇是否还与地面保持垂直，奇怪吗？为什么？到底隐藏着数学上的什么奥秘？由这些亲切真实情景，导出两个平面垂直的判定定理就水到渠成了。

二、利用趣味历史典故创设情境

数学故事、数学典故有时反映了知识形成过程，有时反映了知识点的本质。新教材在数学内容的学习过程中，介绍了有关的数学背景知识、史料。数学家介绍、背景材料等不仅能加深学生对知识的理解，还提高了学生对数学的兴趣及数学审美的能力。

案例4：在等比数列的前n项和公式的教学中，教师可以在课堂上先给同学们讲一下国际象棋起源的小故事：古代印度有一个国王，他拥有至高无上的权利和无比的财富，但他对这样的生活感到厌倦，他渴望新鲜和刺激。一天，一位老人带着自己的发明——国际象棋来见国王。国王见了这个新玩意儿很喜欢，就和老人对弈起来，一连下了四天，国王感到非常满意，就对老人说：“你带给我无穷的乐趣，我要奖赏你，你可以从我这儿得到你所要的任何东西。”老人慢条斯理地说：“你虽然是世界上最富有的人，恐怕也满足不了我的要求。”国王不高兴了，他严厉地说：“说吧，哪怕你要的是半个王国。”于是老人说出了自己的要求：“请在棋盘的第一格上放一粒小麦，在棋盘的第二格上放两粒小麦，在棋盘的第三格上放四粒小麦，在棋盘的第四格上放八粒小麦，就这样每次递增一倍，一直放到六十四格为止。”国王听了大笑起来，他立即命人取来一袋小麦来，按老人说的如数给他。但是一袋小麦很快就完了。国王觉得奇怪，就命人再去取一袋来，接着是第三袋、第四袋……小麦堆积如山，然而离六十四格还远得很。国王的脸色由惊奇逐渐转为阴沉，最后竟勃然大怒。原来，他国库里的小麦已经搬光了，还到不了棋盘上的第五十格。国王认为老人在欺骗他，就下令把老人给杀了。 故事讲完后，教师继续总结:“老人的话没有错，他的要求的确是难以满足的。根据计算，棋盘上六十四个格子小麦的总数是约为2 587亿吨以上，而现在全世界小麦的年产量也达不到这个数字。”在学生的惊叹中，教师再适时导入新课，就会取得理想的效果。

案例5：在相互独立事件同时发生的概率的教学中，教师可以创设如下情境：三个臭皮匠VS诸葛亮，到底谁更厉害？已知诸葛亮解出问题的概率是0.8，臭皮匠老大解出问题的概率是0.5，臭皮匠老二解出问题的概率是0.45，臭皮匠老三解出问题的概率是0.4，且每个人都是独立解题。那么三个臭皮匠中至少有一人解出问题的概率与诸葛亮解出问题的概率相比，哪个更大呢?

案例6：在等差数列求和公式的教学中，本节课要解决的问题就是Sn的表达式。为了让学生积极主动地将新知识纳入已有的认知结构，设计下列问题：问题1、1＋2＋3＋…＋100＝？这是学生小学就已具备的高斯求和知识，学生可以解决。

三、利用数学实验创设情境

新课程标准下，注重学生的实践操作、合作交流、自主探究等。利用数学实验来创设情境，可以让学生感受到数学的乐趣所在，培养学生的合作能力。数学实验是指实验者运用一定的物质手段，在典型的实验环境中或特定的实验条件下所进行的一种数学探索活动。在数学实验中创设情境，可使学生体验、感受“做”数学的乐趣，培养合作交流能力。

案例7：在概率的定义的教学中，课前请同学同位2人一组准备1枚硬币，上课后组织同学们做抛硬币的实验，分为连续抛10次、50次、100次等等。一位同学抛，同位记录正面朝上的次数，同学们做得兴高采烈。做完以后老师适时提问：“若是随机抛一次，正面朝上的概率有多大？请同学们用你的实验记录来解释。”由于学生们全部参与了实验，所以每个人都会从中得到收获。利用数学实验来创设教学情境，可以让学生感受到数学的乐趣所在，培养学生的合作能力。

案例8：在不在一条直线上的三点确定一个圆的教学中，教师先发给每一个学生一张破碎了的圆形硬纸片，并且说：“机器上的皮带轮碎了，为了再制造一个同样大小的皮带轮，请你设法画出皮带轮对应的圆形。”接着让学生用圆规、直尺、量角器等比比画画，进行实验，探索问题的解法。然后在实验的基础上，设置问题情境：过不在一条直线上的三点可以画几个圆？

案例9：在线面垂直的判定定理的教学中，教师可让每个学生准备一块三角形纸片，过顶点A翻折该纸片得到折痕AD，请同学们研究：如何来翻折纸片，才能使折痕AD与桌面垂直呢？学生通过自已动手操作，体会做数学的乐趣，并通过自已的实验，直观地“发现”了线面垂直的判定定理，其对定理的理解会比老师直接给出深刻得多。

创设情境，在课堂教学中的地位不可低估，如能运用自如，则教者听者都会精神振奋，各自进入角色。[3]教师在数学教学过程中要了解学生，善于挖掘教材潜力，紧密联系学生的生活实际，从学生的生活经验和已有知识出发，创设各种情境，为学生提供从事数学活动的机会，从而激发其对数学的学习兴趣。这正是《数学课程标准》的意旨所在。

[1]张晓斌.创设问题情境唤起学生的创新思维[J].数学通报，2011（11）：123-125.

[2]李开慧.关于数学课程的情境化设计[J].中学数学，2007 （9）：44-46.

[3]宋秉信.数学学习论[M].重庆：重庆大学出版社，1990.

[责任编辑陈国平]

葛云虎，男，南京金陵中等专业学校一级教师，主要研究方向为中职数学教学。

G712

A

1674-7747（2016）36-0049-03