导数解决多元问题的几种策略*

□ 赵思林 李世和

（内江师范学院数学与信息科学学院，四川内江 641112；内江市第六中学，四川内江 641112）

导数解决多元问题的几种策略*

□ 赵思林 李世和

（内江师范学院数学与信息科学学院，四川内江 641112；内江市第六中学，四川内江 641112）

导数是非常重要的数学工具，能够解决很多一元问题，也能处理一些多元问题．用导数解决多元问题的常用策略和方法有消元策略、主元策略、换元策略、逐次求导策略、运用琴生不等式策略等．

导数；多元问题；策略

笔者曾向一所国家级示范中学高三实验班的学生提了一个问题：用导数能解决多元问题吗？大多数学生认为不能.分析其原因，可能有三：一是这些学生没有用导数解决多元问题的“经验”；二是很多学生误认为“导数只能解决一元问题”，这显然是受到了思维定式的消极影响；三是学生缺乏解决多元问题的策略性知识.事实上，导数是非常重要的数学工具.导数能够解决很多一元问题，也能处理一些多元问题，比如证明多元不等式、求多元函数的最值等.用导数解决多元问题，既需要以数学思想方法为指导，更需要良好思维策略的灵活运用.

用导数解决多元问题的基本程式是：（1）将多元问题转化为一元问题；（2）构造一元函数；（3）用导数研究函数性态（包括单调性、极值、最值、凹凸性等）；（4）解决原问题.用导数方法解决多元问题具有思路清晰、易于掌握、简洁明快等特点.下面介绍用导数解决多元问题的一些常用策略和方法，如消元策略、主元策略、换元策略、逐次求导策略、运用琴生不等式策略等.

一、消元策略

消元策略是用导数解决多元问题的基本策略.

例1（2009年清华大学自主招生理科试题）（1）x，y为实数，且x+y=1，求证：对于任意整数

分析：对于（1），看似二元，实则一元问题.消去一元如y即变成一元问题.

（2）利用下面例3的结论立即获证，其过程从略.

二、主元策略

主元策略是把多元问题化为一元问题的重要策略.主元策略可极大地拓展导数的应用范围.

例2（2010年江苏卷第21题）设a，b均为非负实数，求证：

思路分析1：这是江苏卷的选做题.通过变形、配凑等过程可以完成证明，但对学生来说，有一定的技巧性，其思路不容易想到.若用主元策略，比如将a看成主变量，b看成常数（参数），就可构造关于a的函数，利用熟悉的导数方法来证明，其解题思路可谓自然清新.

思路分析2：当b=0时，不等式显然成立，以下仅讨论b＞0的情况.

这就将二元问题转化为一元问题了，利用导数就容易解决了，以下从略.

例3设a，b，c∈R+，求证：a3+b3+c3≥3abc.

分析：因本题有3个独立的变量，看似不能用导数证明.但若将a看成主变量，记a=x，并把b、c都看成常数（参数），就可构造关于x的一元函数，利用导数方法可简证之.

三、放缩换元策略

有一些多元问题，可以先用放缩、减元、换元等方法，然后再构造函数，最后利用导数解决问题.

分析：本题是2006年高考数学四川卷理科压轴题的最后一问，当年高考全省无一人用初等方法做出来，难度极高.其关键是证明：2+，也就是要证明：这里若孤立地看问题，则共有4个元：x1，x2，x1+x2，x1x2，此时不能用导数；若用整体思想，则仍有2个元：x1+x2，x1x2，这时仍不能用导数，因此，考虑把x1+x2变为x1x2，事实上，用基本不等式放缩即可实现二元化一元的想法.

四、逐次求导策略

有些多元问题可以分几步变为几个一元问题，每一步都只确定一个自变量，其余字母均看成常数，这就可以用逐次求导策略程式化地解决这些多元问题.

例5（2010年四川卷理科12题）设a＞b＞ c＞0，则的最小值是（ ）.

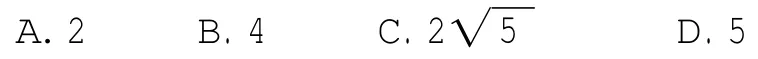
综上，f（c）≥g（b）≥h（a）≥4.故选B.

评注：此题是当年公认的难题，许多教师当时也不会做.这种逐次求导求最值的方法是具有普遍性的方法，它可以程式化地处理一些含有多个变量的最值问题.

五、运用琴生不等式策略

高等数学里有一些工具是专门处理多元问题的，比如，运用琴生不等式、柯西不等式、算术—几何平均不等式等是解决多元问题的重要策略.柯西不等式、算术—几何平均不等式一般不涉及导数，故本文不作讨论.

凸函数（凹函数）定义：设函数f（x）在区间Ⅰ上对任意两点 x1，x2总有则称函数f（x）在区间Ⅰ上为凸函数（或凹函数）.

凸函数（凹函数）的判定定理：设函数f（x）在区间Ⅰ上具有二阶导数，则f（x）为区间Ⅰ上的凸（凹）函数的充要条件是f''（x）≤0（f''（x）≥0）.

琴生不等式：（1）若f为[a，b]上的凸函数，则对任意xi∈[a，b]，则

（2）若f为[a，b]上的凹函数，则对任意xi∈[a，b]，则

例6（2005年全国卷Ⅰ理科22题）（Ⅰ）设函数f（x）=xlog2x+（1-x）log2（1-x），（0＜x＜1）求f（x）的最小值；

评注：本题含有函数凸性的背景.（Ⅱ）的设计意图是充分利用（Ⅰ）的结论，并用数学归纳法来证明，此方法曾有中学老师评论：不容易想，不容易懂，技巧性太强.顺便指出，（Ⅱ）的结论是信息学中的基本定理.

教育部“本科教学工程”四川省地方属高校本科专业综合改革试点项目——内江师范学院数学与应用数学“专业综合改革试点”项目（ZG0464）；四川省“西部卓越中学数学教师协同培养计划”项目.