2016年诺贝尔物理学奖：拓扑相变与物质拓扑相的理论发现*

施郁

复旦大学物理学系，上海 200433

2016年诺贝尔物理学奖：拓扑相变与物质拓扑相的理论发现*

施郁†

复旦大学物理学系，上海 200433

对2016年诺贝尔物理学奖的获奖工作以及背景知识进行了通俗而力求准确的介绍，考察了科学思想的历史发展过程以及三位获奖科学家的经历，最后总结了这次获奖成就的意义以及给我们的启示。

2016年诺贝尔物理学奖；相变；拓扑相变；拓扑相；索利斯；科斯特里兹；霍尔丹

2016年的诺贝尔物理学奖授予大卫·索利斯(David J. Thouless)、邓肯·霍尔丹(F. Duncan M. Haldane)和迈克·科斯特里兹(J. Michael Kosterlitz)，以表彰他们关于拓扑相变和物质拓扑相方面的理论发现。其中，奖金的一半由索利斯获得，另一半由霍尔丹和科斯特里兹均分。

在这篇文章中，笔者用通俗易懂而又力求准确的方式，解释涉及的科学问题，并梳理科学思想的演变。在这之前，我们先介绍一下这三位物理学家。

1 获奖科学家

这三位诺贝尔奖得主都是长期在美国工作的英国人，都是剑桥大学校友，也都是理论物理学家。

索利斯1934年出生于苏格兰的拜尔斯顿(Bearsden)，在英格兰的剑桥长大，因为他的父亲是剑桥大学的心理学家。索利斯就读于著名的温切斯特公学(Winchester College)。这所学校有着600多年的历史，是英国历史最为悠久、具有最好的学术传统的预科学校。

1952年，索利斯进入剑桥大学三一学堂(Trinity Hall)念本科。1955年取得学士学位后，索利斯来到康奈尔大学攻读博士学位，导师是著名物理学家贝特(Hans Bethe)。1958年获博士学位后，索利斯在美国加州的劳伦斯·伯克利实验室工作了一年，然后作为博士后研究员来到英国伯明翰大学，导师是著名物理学家派尔斯(Rudolf E. Peierls)。1961—1965年，索利斯任剑桥大学讲师。1965—1978年，他任伯明翰大学数学物理学教授。1979—1980年在美国耶鲁大学任教授。1980年后在华盛顿大学任教授，2003年荣休。

科斯特里兹1942年生于苏格兰的阿伯丁(Aberdeen)，1962年进入剑桥大学冈维尔与凯斯学院(Gonville and Caius College)。这时，索利斯是剑桥大学讲师，科斯特里兹还听过他的课。

科斯特里兹1965年和1966年在剑桥大学分别获学士和硕士学位，1969年在牛津大学获得博士学位，后去意大利都灵做博士后研究。1971年，科斯特里兹来到伯明翰大学做博士后。他后来在康奈尔大学工作了一段时间后，1974年回到伯明翰大学任教。科斯特里兹1982年也去了美国，任布朗大学教授至今。

霍尔丹1951年生于英国伦敦，在圣保罗学校(St Paul’s School)上学。这是英国最好的学校之一，牛津剑桥录取率最高。1970年，进入剑桥大学基督学院(Christ’s College)。1978年又在剑桥大学获博士学位。导师是当时从贝尔实验室到剑桥大学兼职的著名物理学家安德森(Philip W. Anderson)。安德森是凝聚态物理的大师，1977年与他的导师范弗列克(J. H. van Vleck)及英国物理学家莫特(N. F. Mott)分享诺贝尔物理学奖。霍尔丹取得博士学位后，来到美国。现在他也是普林斯顿大学教授。

2 物质的相与相变

同样的微观粒子组成的物质有不同的宏观表现，这就是相。物质究竟处于哪个相，除了有能量因素外，还有混乱程度的因素。混乱程度叫作熵。熵这个字是老一辈物理学家翻译“entropy”一词的时候发明的字，火字旁表示与热有关，右边的商字表示它是热量与温度的商。准确地说，对于可以定义温度的系统，微小的熵的变化是微小的热量变化与温度的商。所以简单来说，温度乘以熵就得到热量。

热力学第二定律告诉我们，孤立系统的熵总是不减少的，也就是说，熵会不断增加直到最大，然后保持不变。一个系统和它的周围环境之间有热量交换，但是它们共同构成一个孤立系统。根据能量守恒定律(也就是热力学第一定律)，系统内部能量的改变作为热量从环境获得或者传递给环境，而热量除以温度就是环境的熵的改变。由此可以推论出，系统的内部能量减去温度乘以系统的熵(叫做自由能)总是减少，一直到最小值，然后保持不变，这时系统达到平衡状态。这里所说的温度是指绝对温度。绝对零度即“绝对的零度”，是世界上最低的可能的温度，等于零下273.15 °C。只要温度不是绝对零度，熵就要起作用。

因此为了降低自由能到最小，一方面系统的内部能量要尽可能地低，另一方面混乱程度(熵)又要尽可能地高。这决定了在一定温度下物质处于哪个相。也就是说，对于给定的某个温度，哪种相的自由能低，系统就选择哪种相。这也决定了在什么温度发生不同相之间的转变，这就是相变。高于相变温度，系统处于无序相；低于相变温度，系统处于有序相。如果在某个温度下，有序相的自由能比无序相低，那么无序相到有序相的相变就是可以发生的。

一个常用的相变模型是磁模型(图1)。磁体是由很多磁性原子组成的点阵，点阵整体像是一台大型集体舞蹈。每个原子是个小磁体，有类似磁铁的南极到北极的磁性方向。每一对相邻原子之间有个耦合，当它们磁性方向相同或者相反时，耦合的能量最低。遵循前一种规则的叫做铁磁体，后一种叫做反铁磁体。因此，在铁磁体中，所有的原子磁性方向一致时，总能量(也就是所有的邻居对的耦合能量之和)最低。在反铁磁体中，相邻原子磁体的磁性方向相反，犬牙交错时总能量最低。原子之间的磁性耦合原理是海森堡首先提出的。对于原子磁性方向可以指向空间任意方向的情况，磁性模型又叫作海森堡模型。如果每个原子的磁性方向局限一个平面上，相邻原子的磁性耦合能取决于它们磁性方向在这个平面上的夹角，这样的磁性模型叫XY模型。

同样是这些原子，它们的磁性方向却有各种可能。如果温度不是绝对零度，因为要兼顾混乱度的要求，这些原子的磁性方向可能满足不了能量最低的要求，也就是做不到完全相同或者相反。因此它们的总和，也就是整个磁体的磁性，有可能有一定大小，朝向某个方向；但也有可能为零，因为各个原子不同的方向可能互相抵消了。

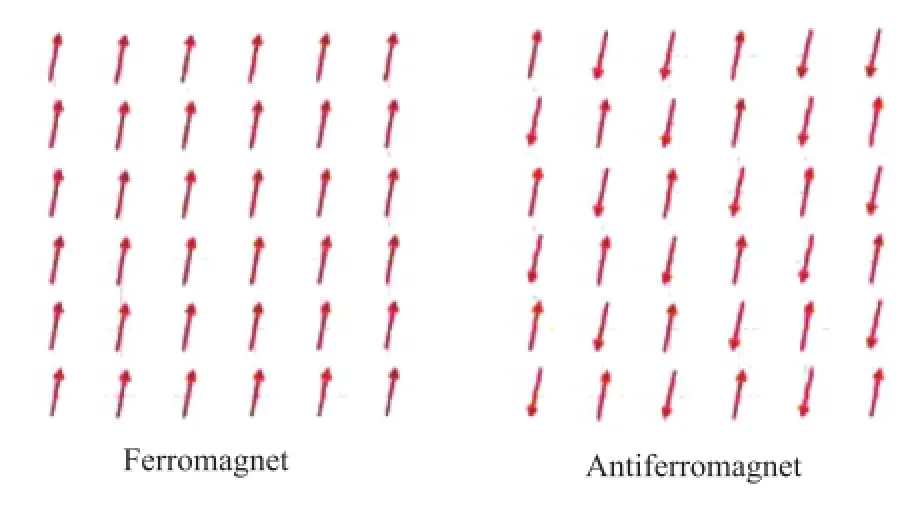
图1 铁磁体(左)与反铁磁体(右)示意图(图片来源：Nobelprize.org)

如果每个原子的磁性方向可以在三维空间中指向任意方向，那么铁磁体在某个温度以下有个总的磁性，也就是说，各个原子的磁性加起来不为零，指向某个方向，这个有序相叫铁磁相。在某个温度以上，各个原子的磁性方向是混乱的，磁性互相抵消，整个铁磁体的磁性为零，这个无序相叫顺磁相。

相变能否发生，还与系统的维度有关。通常的物体有长、宽、高三维。如果构成物体的粒子只能在一个面上运动，就是二维。如果构成物体的粒子只能在一条线上运动，就是一维。1966年，康奈尔大学的默敏(D. Mermin)和瓦格纳(H. Wagner)[1]以及贝尔实验室的霍亨贝格(P. Hohenberg)[2]证明，如果物理特性(比如磁性方向)可以连续变化，那么只要温度不是绝对零度，二维或二维以下不发生相变，因为这时混乱程度总能战胜能量的改变。韦格纳(F. Wegner)也专门针对二维XY模型，严格证明了在绝对零度以上没有相变[3]。

但是伊辛模型是一种特殊的磁体模型，其中每个原子的磁性方向不是空间或平面上的任意方向，而只能是上下两个方向。对于伊辛模型，上面关于相变的结论有所改变，一维没有相变，但是二维有相变。这正是索利斯的博士后导师派尔斯在1936年证明的[4]。

3 索利斯与科斯特里兹提出拓扑相变

1971年，科斯特里兹来伯明翰做博士后时，索利斯正在伯明翰上一门关于超流与超导的研究生课程[5]。超流是没有黏滞的流体现象，液态氦在极低温时就是超流体。超导是电子的超流，因为带电，所以是电阻为零的导电。虽然超流和超导的微观机制要用到量子力学，但是相变行为可以用前面所解释的能量与混乱度的竞争来描述，不需要量子力学。

索利斯开的课程介绍了理论上的超流薄膜，也就是二维超流，它的相变性质与二维XY模型是类似的。根据上面说的相变对维度的依赖，二维XY在绝对零度之上没有相变。索利斯在解释理论上超流薄膜的涡旋能量时，意识到涡旋可能引起相变。

索利斯和科斯特里兹合作研究了二维系统相变的可能[6-8]。他们发现，涡旋扮演关键角色。涡旋是绕着一个点或者一个轴的流动，或者某种物理性质(比如XY磁模型中不同原子的磁性方向) 随角度变化。有两种可能的相，高温相是有自由的涡旋，低温相是旋转方向相反的涡旋两两束缚成对(图2)。随着温度的不同，这两个相的自由能谁高谁低会发生变化，导致在绝对零度之上的某个温度发生相变。

图2 左图：一个单独的涡旋；右图：一个涡旋对(图片来源：Nobelprize.org)

这个研究工作就是2016年诺贝尔奖所嘉奖的拓扑相变，又以他们的姓氏首字母命名为KT相变或被称为科斯特里兹-索利斯相变。

拓扑相变这一名词源于涡旋的拓扑结构。拓扑是指在局部的连续变化下保持不变的整体性质。假设你用橡皮泥捏一个轮胎状的东西，你可以拉伸、扭曲、变形，把它变为奇形怪状的东西，但是始终有一个洞在那里，这就是拓扑不变量。

涡旋的拓扑不变可以如下理解：假设你围绕一个点或者一个轴走动，回到原地，不管路径怎样五花八门，总归是绕了整数圈数。这个圈数不依赖于路径的细节，是个拓扑数，术语叫做缠绕数。涡旋就由它的缠绕数表征。

在索利斯和科斯特里兹发现拓扑相变前一年，苏联的贝热津斯基(Vadim Berezinskii，1981年去世)提出XY模型中涡旋激发的重要性[9-10]。大概由于有些科学家对贝热津斯基工作的强调，KT相变还被称为BKT相变。但是，其实贝热津斯基没有得出相变的结论。

相变规律具有普适性，在不同系统中存在同样的定量规律，KT相变也是如此。索利斯和科斯特里兹的这个工作使人们认识到二维薄层材料也可以有超流、超导以及其他有序相。

4 量子霍尔效应的拓扑

霍尔效应是美国物理学家霍尔(Edwin Hall)在1897年发现的，指电子在电压驱动下形成电流时，再加上一个垂直的磁场，由于电场和磁场的共同作用，电子偏离原来的电压方向，并在导体边缘累积，从而在垂直于电流的方向形成新的电压，叫做霍尔电压。

量子霍尔效应自从1980年被发现后，一直是凝聚态物理的重要课题，曾两次获诺贝尔奖青睐。最初的发现者冯·克里青(Klaus von Klitzing)做出发现5年之后就得奖了[11]。

量子霍尔效应(图3)是二维电子气的行为。二维电子气在两种不同的半导体的界面形成，电子局限在这个二维平面上运动。在低温下，二维电子气的霍尔效应出现量子化，也就是说，电流与霍尔电压的比值总是某个常数(e2/h，其中e是电子电荷，h是代表量子力学效应的普朗克常数)的整数倍。这个整数非常精确，精确度达到十亿分之一，而且在一定范围内改变实验参数时保持不变。如果磁场改变达到一定程度，量子化的整数跳到下一个整数。那个常数的倒数，即e2/h，等于 25 812.807 557 Ω，被命名为冯·克里青常数，已成为电阻的标准。

图3 量子霍尔效应(图片来源：Nobelprize.org)

20世纪80年代，在华盛顿大学，索利斯与合作者提出，量子霍尔效应的量子化起源于拓扑，对应的整数是所谓“陈省身数”[11-12]。这是华人数学家陈省身先生很多年前发现的一个表征拓扑性质的数，是一种特殊的缠绕数，代表了空间的弯曲程度。但是对于量子霍尔效应来说，这个空间是电子的量子波函数构成的闭合抽象空间。这就是索利斯获得诺贝尔奖的另一部分成就。

5 霍尔丹的贡献

在索利斯等人提出量子霍尔效应的拓扑本质后，1988年，霍尔丹提出一个模型，其中没有磁场，但是也能实现量子霍尔效应，因为用另外的方法实现了所需要的拓扑性质[13]。这是霍尔丹的一部分获奖成就。无磁场的量子霍尔效应现在称作反常量子霍尔效应。

霍尔丹的另一部分获奖成就是他1982年关于量子一维海森堡反铁磁体的结论。按前面的介绍，一维海森堡反铁磁体就是说，每个原子与相邻原子磁性方向相反时，这对邻居的耦合能量最低。但是前面讨论的模型中没有量子力学，霍尔丹研究的是量子力学起作用时的模型，计算各种可能的能量取值。

量子力学使得问题复杂化，因为量子力学里有个著名的海森堡不确定关系，使得原子磁性方向不确定。不过，对于一维铁磁体，最低能量状态仍然是所有原子磁性方向一致。在此基础上的激发类似于声波，也就是说无论多小的能量都能激发一个磁性波在原子间传播。简单的近似计算给出，对于一维反铁磁，最低能量状态是所有原子的磁性方向犬牙交错，在此基础上也能激发能量可以任意小的磁性波。

刻画原子磁性的特征量(称作磁矩)要么是某个常数(玻尔磁矩)的整数倍，要么是半整数倍，这个倍数叫作自旋。所以一维磁体又叫自旋链，磁性波也叫自旋波。索利斯的导师贝特在1931年严格地解出了自旋等于1/2的情况[14]。从杨振宁和杨振平1966年的一篇文章开始[15]，贝特的方法被称作贝特假设。严格的最低能量态并不是犬牙交错态，但是确实能激发能量可以任意小的自旋波。

那么对于自旋是其他整数或半整数的情况，以上自旋波结论是否正确呢？霍尔丹发现，对于自旋是半整数的情况(1/2、3/2、5/2等等)，结论与1/2类似。但是对于自旋是整数的情况(1、2、3等等)，结论则截然不同，能量必须大于某个非零值，才能有激发[16-17]。霍尔丹的结论后来得到实验证实。

他的论证用到一维时间与一维空间组成的抽象二维空间里的一个拓扑缠绕数。对于整数自旋情况，各种缠绕数的拓扑效应都不起作用(后来人们发现对于磁体的边界有影响)，结果量子力学不确定关系导致磁体的最低能量态和激发态之间有一个不等于零的差别，所以不能有能量任意小的自旋波。对于半整数情况，偶数缠绕数和奇数缠绕数带来的效应互相抵消，结果导致有能量可以任意小的自旋波。

霍尔丹的两个获奖工作都与目前的热门领域拓扑绝缘体关系密切。

6 意义与启示

三人的工作将凝聚态物理带到了一个新的天地，带来了革命性的新观念，打开了组成物质的大量粒子微观拓扑性质与物质宏观物理性质关系的大门。他们开辟的这个方向现在已经成为一个前沿和主流领域，而且对材料科学和信息科学有很大的影响，为新材料、新器件的设计带来了新的思路。对于量子计算机的实现也很有意义，因为拓扑的性质可能带来稳定的量子状态，帮助克服量子计算对于环境扰动的敏感。

从这三位科学家的道路中，笔者总结了几条启示，与大家分享：

首先，追求卓越。前面提到，索利斯在中学就表现出追求卓越、不满足于最低要求。三位获奖者事业上的经历也体现出了这一点。

第二，不囿于成规，勇于创新。不是简单否定，而是另辟蹊径。拓扑相变之于普通相变，整数自旋链之于半整数自旋链，这些创新都是突破了原来的范式，但是又不否定适用于各自范畴的原来的理论 。

第三，他们的研究工作是研究本身和好奇心驱动的。值得注意的是，除了索利斯等人揭示量子霍尔效应的拓扑，他们的获奖工作都是领先于实验的理论研究。关于量子霍尔效应的拓扑虽然是在量子霍尔效应发现之后，但是它激发了进一步的实验和工作。这些理论上的成功对于理论工作者是一个鼓舞。

第四，三位科学家都有特立独行的风格。他们的研究并非为了赶时髦、追乐队花车，他们的成果后来却引导了主流和热门领域。

第五，他们的道路反映了优秀的科学传统的积累和传承。笔者注意到，2016年三位获奖科学家分属两个“师生三代获得诺贝尔物理学奖”的系列，一个是贝特—索利斯—科斯特里兹，另一个是范弗列克—安德森—霍尔丹。

最后，他们三位都是长期在美国工作的英国人，分享2003年诺贝尔物理学奖的莱格特(Anthony J. Leggett)也是英国人，1983年从英国移居美国工作，是美国伊利诺伊州立大学教授(他得奖时，笔者正是他的访问学者)。由此可以看到那些年英国人才流失的严重。中国香港的高锟获得2009年诺贝尔物理学奖的工作，是1966年在英国国际电话电报公司(ITT)的英国分公司标准电话电缆公司(STC)完成的，后来他去香港中文大学兼职，然后又去ITT的美国分公司任职，最后又去香港中文大学。大概20世纪90年代开始，英国也吸引人才流入，达到一种平衡。获得2010年诺贝尔物理学奖的盖姆(A. Geim)和诺沃谢诺夫(K. Novoselov)在英国曼彻斯特大学工作，最初都来自俄罗斯。

7 祝福索利斯教授

笔者在剑桥大学工作期间，2000年曾经与来访的索利斯教授有过比较深入的学术讨论，并请他评阅我当时正在写作的一篇论文草稿。索利斯教授后来从美国发电子邮件给笔者，说在飞机上又想了我的问题，而且仔细读了我的草稿，并提出了重要的建议。

2007年10月31日至11月3日，在新加坡召开的庆祝杨振宁先生85岁寿辰的学术研讨会上，我见到了索利斯。索利斯在会上作了个凝聚态中的拓扑量子数的综述报告。我还记得，我国某位物理学家做报告时，索利斯是主持人，到了规定时间时，他很有原则性地要求报告人停止。会议期间我还与他聊到前一年和当年的诺贝尔奖，并预祝他得到诺贝尔奖。

索利斯夫妇现在住在故乡剑桥。笔者前段时间发邮件给索利斯，祝贺他获得实至名归、姗姗来迟的诺贝尔奖。以他和家人名义的回信提到索利斯目前有点健康问题，还说：“大卫获悉得诺贝尔奖，感到感动和光荣，而且很高兴与科斯特里兹和霍尔丹分享。他感激世界各地的朋友和同事的祝贺和对他对物理学的贡献的赞美(David was moved and honored to learn of the Nobel Prize, and he was delighted to hear that he would share it with Mike Kosterlitz and Duncan Haldane. He is grateful to all his friends and colleagues around the world who have sent congratulations and made such lovely comments about his contributions to physics)。”

让我们期待索利斯教授12月份在斯德哥尔摩从瑞典国王手中接过诺贝尔奖章的时刻。

(2016年11月17日收稿)

[1] MERMIN N D, WAGNER H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models [J]. Physical Review Letters, 1966, 17(22): 1133-1136.

[2] HOHENBERG P C. Existence of long-range order in one and two dimensions [J]. Physical Review, 1967, 158: 383-386.

[3] WEGNER F. Spin-ordering in a planar classical Heisenberg model [J]. Zeitschrift für Physik A Hadrons Nuclei, 1967, 206 (5): 465-470.

[4] PEIERLS M R. On Ising’s model of ferromagnetism [J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1936, 32(3): 477-481.

[5] KOSTERLITZ J M, THOULESS D J. Early work on defect driven phase transitions[M]//JOSE J. 40 years of Berezinskii-Kosterlitz-Thouless Theory. Singapore: World Scientifc, 2013.

[6] KOSTERLITZ J M, THOULESS D J. Long range order and metastability in two dimensional solids and superfuids [J]. Journal of Physics C: Solid State Physics, 1972, 5(11): L124-L126.

[7] KOSTERLITZ J M, THOULESS D J. Ordering, metastability and phase transitions in two-dimensional systems [J]. Journal of Physics C: Solid State Physics, 1873, 6(7): 1181-1203.

[8] KOSTERLITZ J M. The critical properties of the two-dimensional xy model [J]. Journal of Physics C: Solid State Physics, 1974, 7(6): 1046-1060.

[9] BEREZINSKII V L. Destruction of long-range order in onedimensional and two-dimensional systems having a continuous symmetry group I. classical systems [J]. Soviet Journal of Experimental and Theoretical Physics, 1971, 32: 493-500.

[10] BEREZINSKII V L. Destruction of long-range order in onedimensional and two-dimensional systems possessing a continuous symmetry group. ii. quantum systems [J]. Soviet Journal of Experimental and Theoretical Physics, 1972, 34: 610-616.

[11] THOULESS D J, KOHMOTO M, NIGHTINGALE M P, et al. Quantized hall conductance in a two-dimensional periodic potential [J]. Physical Review Letters, 1982, 49(6): 405-408.

[12] NIU Q, THOULESS D J, WU Y. Quantized hall conductance as a topological invariant [J]. Physical Review B, 1985, 31(6):3372-3377.

[13] HALDANE F D M. Model for a quantum hall effect without landau levels: condensed-matter realization of the “parity anomaly” [J]. Physical Review Letters, 1988, 61(18): 2015-2018.

[14] BETHE H. Zur Theorie der Metalle: I. Eigenwerte und Eigenfunktionen der linearen Atomkette [J]. Z Phys, 1931, 71: 205-231.

[15] YANG C P, YANG C N. One-dimensional chain of anisotropic spinspin ineractions [J]. Physical Review, 1966, 150(1): 327-339.

[16] HALDANE F D M. Continuum dynamics of the 1-D Heisenberg antiferromagnet:identifcation with the O(3) nonlinear sigma model [J]. Physics Letters A, 1983, 93(9): 464-468.

[17] HALDANE F D M. Nonlinear field theory of large-spin heisenberg antiferromagnets: Semiclassically quantized solitons of the onedimensional easy-axis Néel state [J]. Physical Review Letters, 1983, 50(15): 1153-1156.

(编辑：温文)

2016 Nobel Prize in Physics: Theoretical discoveries in topological phase transitions and topological phases of matter

SHI Yu
Department of Physics, Fudan University, Shanghai 200433, China

A popular accurate introduction is made for the prize-winning work and related background knowledge for 2016 Nobel Prize in Physics. The historical development leading to these theoretical discoveries and the careers of the three Nobel Laureates are also investigated. The paper is concluded with the implications of these achievements as well as the lessons we can learn.

2016 Nobel Prize in Physics, phase transition, topological phase transition, topological phases, Thouless, Kosterlitz, Haldane

10.3969/j.issn.0253-9608.2016.06.004

*国家自然科学基金面上项目(11374060)资助

†通信作者，E-mail: yushi@fudan.edu.cn