摆式调谐质量阻尼器频率调节新方法①

汪志昊， 郜 辉， 张 闯， 刘 飞

(华北水利水电大学土木与交通学院， 河南 郑州 450045)

摆式调谐质量阻尼器频率调节新方法①

汪志昊， 郜 辉， 张 闯， 刘 飞

(华北水利水电大学土木与交通学院， 河南 郑州 450045)

针对大型摆式调谐质量阻尼器(PTMD)频率调节较难的问题，提出了一种基于永磁体作用力的频率调节新方法，即在PTMD上附加安装永磁体刚度调节装置，通过调整永磁体产生附加刚度的正负与大小，改变PTMD的等效刚度，继而实现PTMD频率的双向调节。基于拉格朗日方程建立了PTMD与永磁体刚度调节装置耦合系统的运动微分方程，阐述了该频率调节方法的可行性，以及PTMD振动频率随幅值的定性变化规律，最后开展模型试验进一步验证与明确了永磁体作用力对PTMD频率的调节机理。理论分析与试验结果表明：当摆式PTMD质量块两侧均布置相吸永磁体时，PTMD频率降低；当布置相斥永磁体时，PTMD频率增大；PTMD频率调节初步设计时，永磁体作用力的附加刚度理论计算值宜适当折减后作为实际等效刚度，该折减系数可偏保守的取为0.5。

振动控制； 调谐质量阻尼器； 频率调节； 拉格朗日方程； 等效刚度

引 言

调谐质量阻尼器(TMD)对风敏感结构振动控制效果突出，已在高耸建筑与大跨度桥梁结构得到广泛应用[1-3]。TMD主要由质量块、调谐频率的弹性元件与耗散结构振动能量的阻尼元件三大组件构成。适用于超高层建筑、高耸电视塔等结构风致振动控制的TMD主要是采用摆式结构作为弹性元件的摆式TMD，尤其是具有形式简单、设计简便、单台TMD就可实现结构多向振动控制等优点的单摆式TMD[4]。摆式TMD在超高层建筑结构的典型应用有：台北101大楼风致振动控制，TMD运动质量块660 t，由8组长11.5 m、直径90 mm的高强度钢索悬吊支承于该大楼的92层结构[5]；上海中心风致振动控制，TMD运动质量块重量高达1000 t，采用12根、长25 m的钢索悬挂[6]。

摆式TMD还常应用于大跨度斜拉桥悬臂施工阶段主梁的风致振动控制[7]，此时TMD需要根据施工进度不断调整频率以适应结构目标控制模态自振频率的变化。此外，一方面由于TMD设计、制造误差以及结构自振频率计算误差等因素，TMD安装过程中需要对自身频率进行调整使其接近于结构自振频率；另一方面在TMD长期运营中，也有必要对TMD的频率进行适当调整，以避免TMD频率失谐带来的减振效果下降[8]。因此，摆式TMD的频率调节显得尤为重要。目前，摆式TMD频率调整方法主要有：设置被动式摆长调节机构[9]、主动自适应式摆长调节机构[10]、附加调频弹簧[11]等。但摆长调节机构复杂，且占用空间大；而调频弹簧仅能增大TMD频率，无法降低既有TMD频率。

受永磁式电涡流阻尼TMD[12]与振动能量回收领域谐振频率调节技术[13-14]的启发，本文拟提出一种基于永磁体作用力的摆式TMD频率调节方法，其核心思想是将永磁体设置在摆式TMD的质量块与主体结构之间，构成永磁式刚度调节装置，利用永磁体同性相斥、异性相吸的特点，改变TMD质量块在摆动过程中回复力的大小，即通过改变TMD的等效刚度实现TMD频率的调节。永磁式刚度装置(弹簧)具有无机械接触、无磨损、寿命长、噪声小，以及刚度调节方便等优点，在机电领域研究与应用较多。文献[15-16]研究分析了永磁式刚度装置的力学特性，文献[17-18]将永磁式刚度装置应用于压电式微振动能量回收，文献[19]将永磁式刚度装置应用于超精密加工所需的隔振器。

本文尝试将永磁式刚度装置应用于工程结构振动控制领域，综合理论分析和模型试验对基于永磁体作用力的摆式TMD频率调节方法进行了可行性研究。

1 基于永磁体作用力的摆式TMD频率调节原理

由摆式TMD振动频率f计算公式

(1)

式中k，m分别表示摆式TMD的回复力刚度与摆动质量。可见，当质量不变时，欲调节TMD频率，只能改变TMD刚度。如图1所示，附加永磁体作用力频率调节装置的摆式TMD由与主结构体连接的吊索、吊挂在吊索下端部的运动质量块、设置在质量块与结构体之间的黏滞阻尼器，以及基于永磁体作用力的刚度调节装置组成；当进行低频调节时，刚度调节装置包括n块设置在质量块侧面上的极性为N极/S极的永磁体和n块设置在该侧面对应的主结构体上的极性为S极/N极的永磁体。

当图1中TMD运动质量块摆动到任意位置时，质量块两侧永磁体吸引力的差值将使得永磁体作用力永远背离平衡位置，从而降低了质量块往复振动的回复力，即减小了TMD的等效刚度，使得TMD频率降低。同理，当质量块两侧永磁体相互排斥时，将使TMD频率增大。

图1 摆式TMD频率调节原理示意图Fig.1 Principle diagram of frequency tuning method for a pendulum TMD

2 摆式TMD频率调节方法的理论研究

2.1 摆式TMD与永磁体刚度调节装置耦合系统的运动微分方程

由于摆式TMD的对称性，可仅取TMD运动右侧运动时进行研究。摆式TMD坐标系定义见图2所示，相应受力简图见图3。

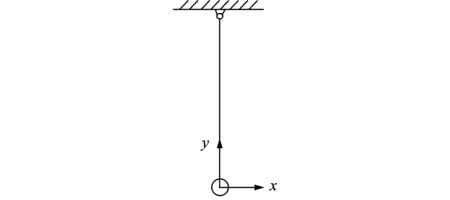
图2 摆式TMD坐标系Fig.2 The coordinate system of a pendulum TMD

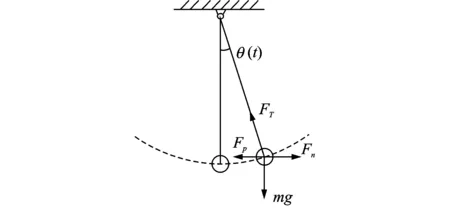
图3 摆式TMD受力示意图Fig.3 The force diagram of a pendulum TMD

此时TMD运动质量块的运动状态由下面的式子给出：

x=lsinθ(t)

(2)

y=l(1-cosθ(t))

(3)

(4)

(5)

式中 x，y表示TMD质量块的位置坐标，l表示TMD摆长，θ表示摆角。

摆式TMD系统所具有的动能T为

(6)

重力引起的势能V

V=mgl(1-cosθ)

(7)

非保守广义力Q

Q=-(Fp-Fn)lcosθ

(8)

式中 Fp表示增加系统回复力的永磁体作用力，Fn表示减小系统回复力的永磁体作用力。

当质量块两侧的永磁体相互吸引时：

(9)

(10)

当质量块两侧的永磁体相互排斥时：

(11)

(12)

式中 Br,Am，δ与r分别表示永磁体的剩磁感应强度、有效充磁面面积、充磁长度(永磁体厚度)与充磁面半径，μ0表示真空磁导率，d0表示TMD处于平衡位置时同组永磁体之间的水平净距。

将式(6)～(12)代入拉格朗日方程

(13)

得到摆式TMD与永磁体刚度调节装置耦合系统的自由振动微分方程

(14)

由于摆角θ很小，可近似地取sinθ≈θ，cosθ≈1，则式(14)简化为

(15)

2.2 基于永磁体作用力频率调节方法的可行性研究

附加永磁体作用力频率调节装置的摆式TMD系统回复力

(16)

则TMD等效刚度

(17)

令

ke=kl+kmag

(18)

其中，摆长l对应的TMD初始刚度

(19)

永磁体作用力产生的附加刚度

kmag=kp-kn

(20)

当摆式TMD运动质量块两侧永磁体相互吸引时

(21)

(22)

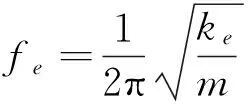
同理，当摆式TMD运动质量块两侧永磁体相互排斥时：

(23)

(24)

由于kp>kn，kmag=kp-kn>0，则ke=kl+kmag>kl，即当摆式TMD运动质量块两侧永磁体相互排斥时，会使TMD等效刚度增加，此时TMD频率将增大。

2.3 永磁体作用力附加刚度与振幅的关系

为确定永磁体作用力的频率调节范围，首先需要确定永磁体作用力附加刚度kmag。影响kmag的主要因素有：永磁体的型号与尺寸，永磁体的组数n，质量块在平衡位置时永磁体之间的净距d0，以及摆式TMD的最大位移幅值A。当影响永磁体作用力附加刚度各个变量的取值如表1所示时，根据式(20)～(24)计算得到永磁体作用力附加刚度随振动位移的变化曲线如图4所示。

表1 永磁体刚度调节装置相关参数取值

Tab.1 Parameter values of stiffness adjusting device with permanent magnets

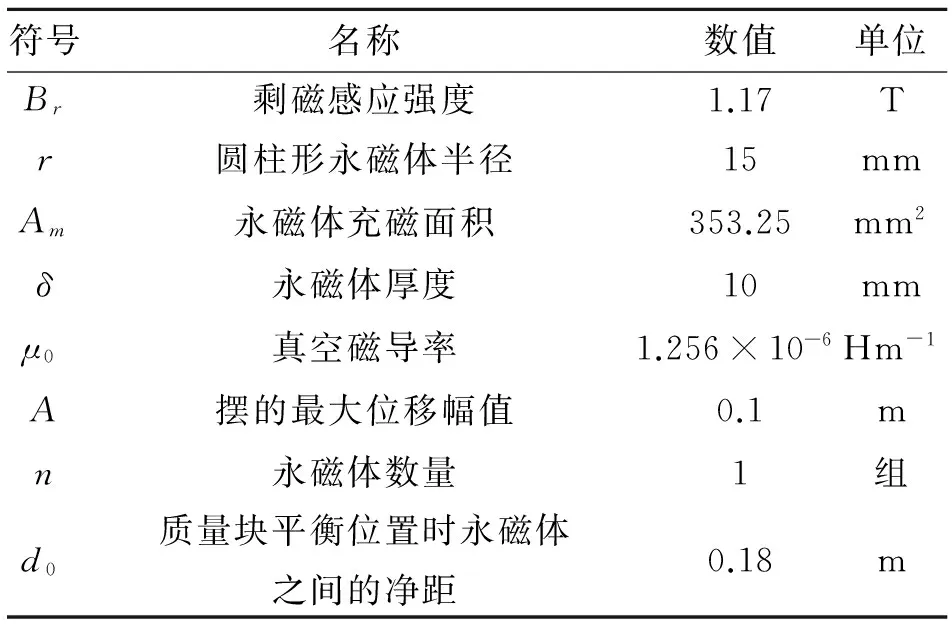
符号名称数值单位Br剩磁感应强度1.17Tr圆柱形永磁体半径15mmAm永磁体充磁面积353.25mm2δ永磁体厚度10mmμ0真空磁导率1.256×10-6Hm-1A摆的最大位移幅值0.1mn永磁体数量1组d0质量块平衡位置时永磁体之间的净距0.18m

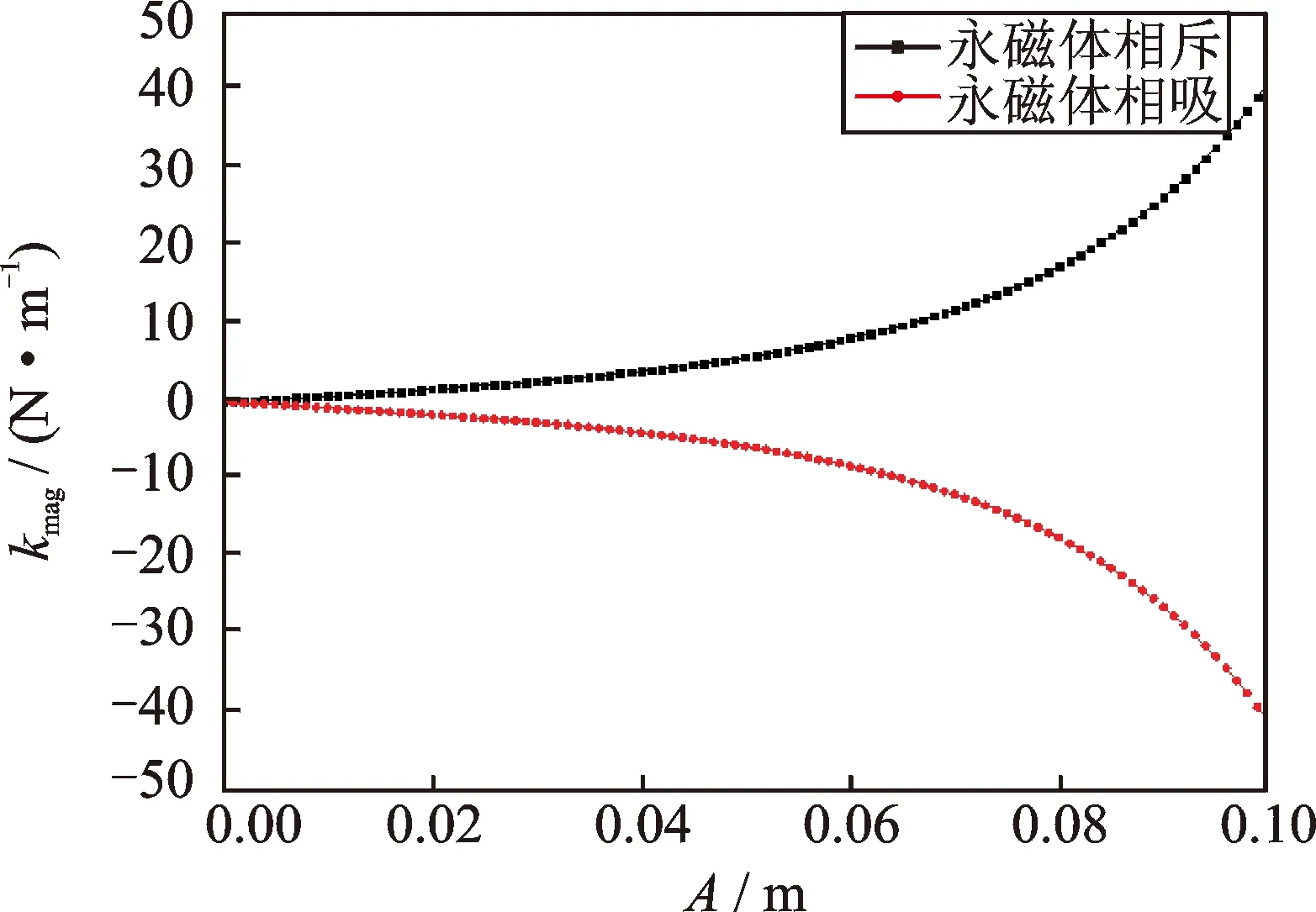
图4 永磁体作用力附加刚度随振动位移变化曲线Fig.4 Plot of the supplemental stiffness generated by permanent magnets versus vibration displacement

从图4中可以看出永磁体作用力产生的附加刚度规律：当质量块两侧布置的永磁体相互排斥时，永磁体产生的附加刚度为正，且附加刚度随着振动位移的增大而增大，最大振幅时永磁体的附加刚度达到正的最大值，此时TMD等效刚度随振幅的增大而增大，即振动频率将随振幅增大而增大；当质量块两侧布置相吸的永磁体时，永磁体产生的附加刚度为负，且附加刚度随着振动位移的增大而增大，最大振幅时永磁体的附加刚度达到负的最大值，此时TMD等效刚度随振幅的增大而减小，即振动频率将随振幅增大而减小。

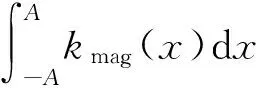
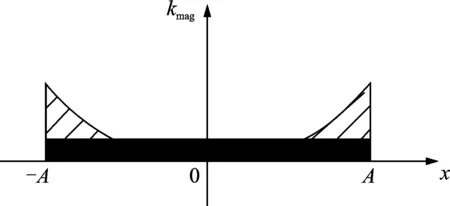
图5 永磁体作用力附加等效刚度理论值计算示意图Fig.5 Theoretical calculation schematic of supplemental equivalent stiffness generated by permanent magnets

据此得到永磁体作用力产生的附加等效刚度的计算表达式

(25)

按照表1的参数取值，永磁体作用力产生的附加等效刚度理论预测值为

(26)

为方便计算，永磁体作用力产生的附加等效刚度可表示为

kmag,e=ηkmag(A)

(27)

式中 η表示无量纲系数(从图5可以看出，η必然小于0.5)，kmag(A)表示最大振幅时永磁体作用力产生的附加刚度。当相关参数按表1取值时，计算得到η=0.24。

2.4 附加永磁体刚度调节装置的TMD调频设计

本文提出的摆式TMD频率调节方法，可以实现TMD频率的双向调节，具体调节步骤如下：

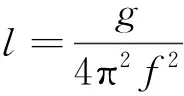
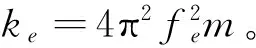
(3)计算永磁体作用力刚度调节装置的附加等效刚度目标值ks=ke-kl。

(4)进行刚度调节装置的细节设计：

①选取圆柱形永磁体，确定具体尺寸参数r，Am，δ与Br；

②根据TMD振幅A初选一个较大的d0，且d0>A；

③利用式(25)确定质量块两侧对称布置1组永磁体产生的附加等效刚度kmag,e；

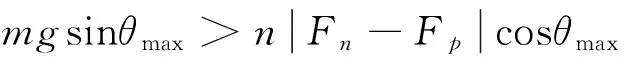
(5)试验测试TMD的频率实际调节值，若实测调节值偏小，可通过微调增大d0减小附加刚度，若实测值偏大，可通过微调减小d0增大附加刚度。

3 摆式TMD模型频率调节试验

3.1 试验模型

试验模型永磁体刚度调节装置相关参数取值见表1。

(1)模型TMD摆长为1.83 m(基频为0.3685 Hz)，运动质量块质量10 kg，摆长对应的初始刚度kl=53.55 N/m，TMD设计振幅为0.1 m。

(2)取TMD频率调节范围为15%(此处仅为阐述TMD频率调节方法的可行性，实际工程应用宜取为5%)，则刚度调节装置的附加刚度ks=17.1 N/m，为使试验过程中试验装置保持稳定，试验支撑结构采用梯形四柱框架，支撑结构总高度2.1 m，质量块通过四根吊索对称悬挂在顶板的中间区域。

(3)永磁体采用N35型钕铁硼(NdFeB)，具体相关参数见表1。由2.3节可知，单组永磁体产生的附加等效刚度kmag,e=9.76 N/m。据此计算得到永磁体的组数n=1.75，取n=2进行模型试验验证。永磁体布置方法见图6，通过改变永磁体的组数和极性，研究永磁体作用力对TMD频率的调节规律，并根据试验结果对永磁体产生的附加等效刚度进行修正。

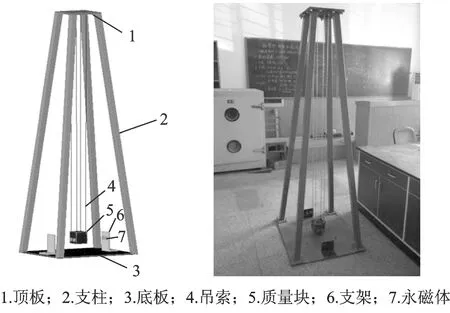
图6 摆式TMD试验模型Fig.6 Test model of a pendulum TMD

3.2 试验方法

采用人工施加初位移的方法对摆式TMD进行激振，每次试验均使TMD质量块从相同初始位移下自由释放，通过891-4型速度传感器测试TMD振动速度，采用江苏东华动态采集系统DH5935N以500 Hz的采样频率对振动速度信号进行动态采集，分析TMD振动频率随位移的变化规律。试验工况汇总见表2。

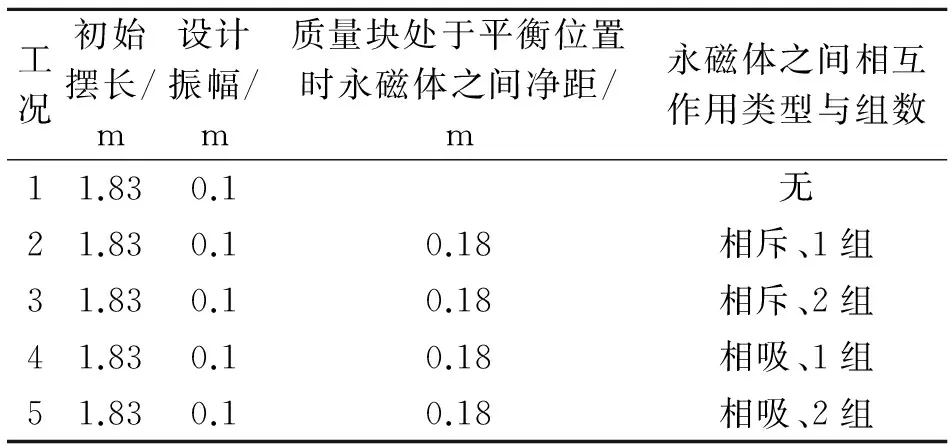
表2 摆式TMD试验工况一览表

4 试验结果与分析

4.1 TMD自由振动时程

从图7,8与9分别给出的工况1,3与5自由振动速度时程曲线可以看出：工况5摆式TMD质量块速度峰值最小，工况1次之，工况3最大。由于各工况初始位移幅值A相同，由速度峰值vmax=2πfA推断，工况5频率最低，工况1次之，工况3最高。与前文理论定性分析结果完全一致，试验结果也表明：当摆式TMD运动质量两侧永磁体相吸时，TMD频率低于初始频率；当摆式TMD运动质量两侧永磁体相斥时，TMD频率高于初始频率。

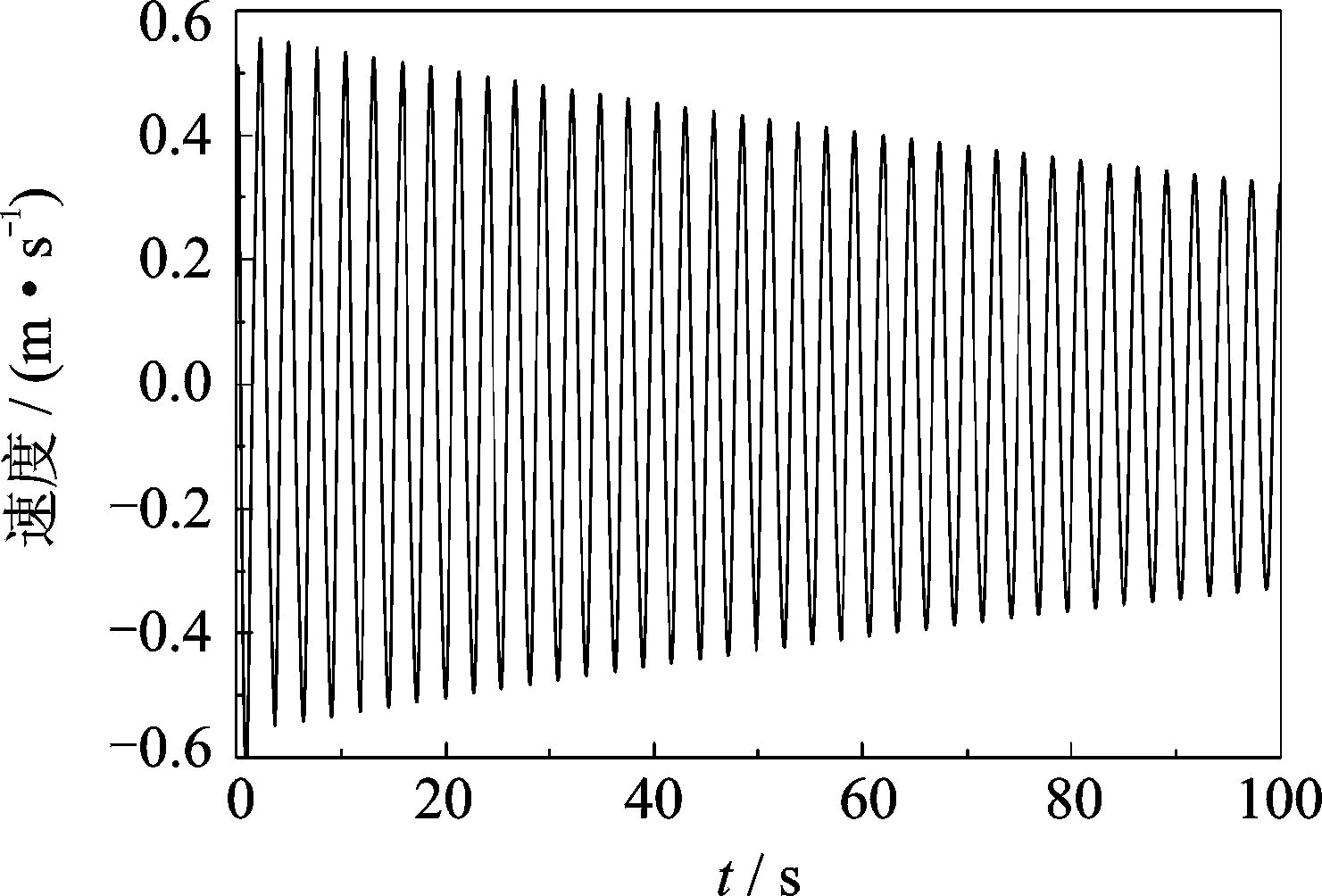
图7 工况1 TMD自由衰减振动速度时间历程曲线Fig.7 The free vibration time histories of the TMD′s velocity for experimental case 1

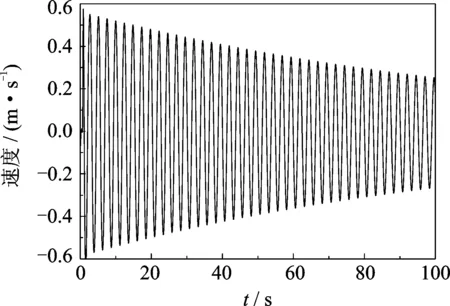
图8 工况3 TMD自由衰减振动速度时间历程曲线Fig.8 The free vibration time histories of the TMD for experimental case 3

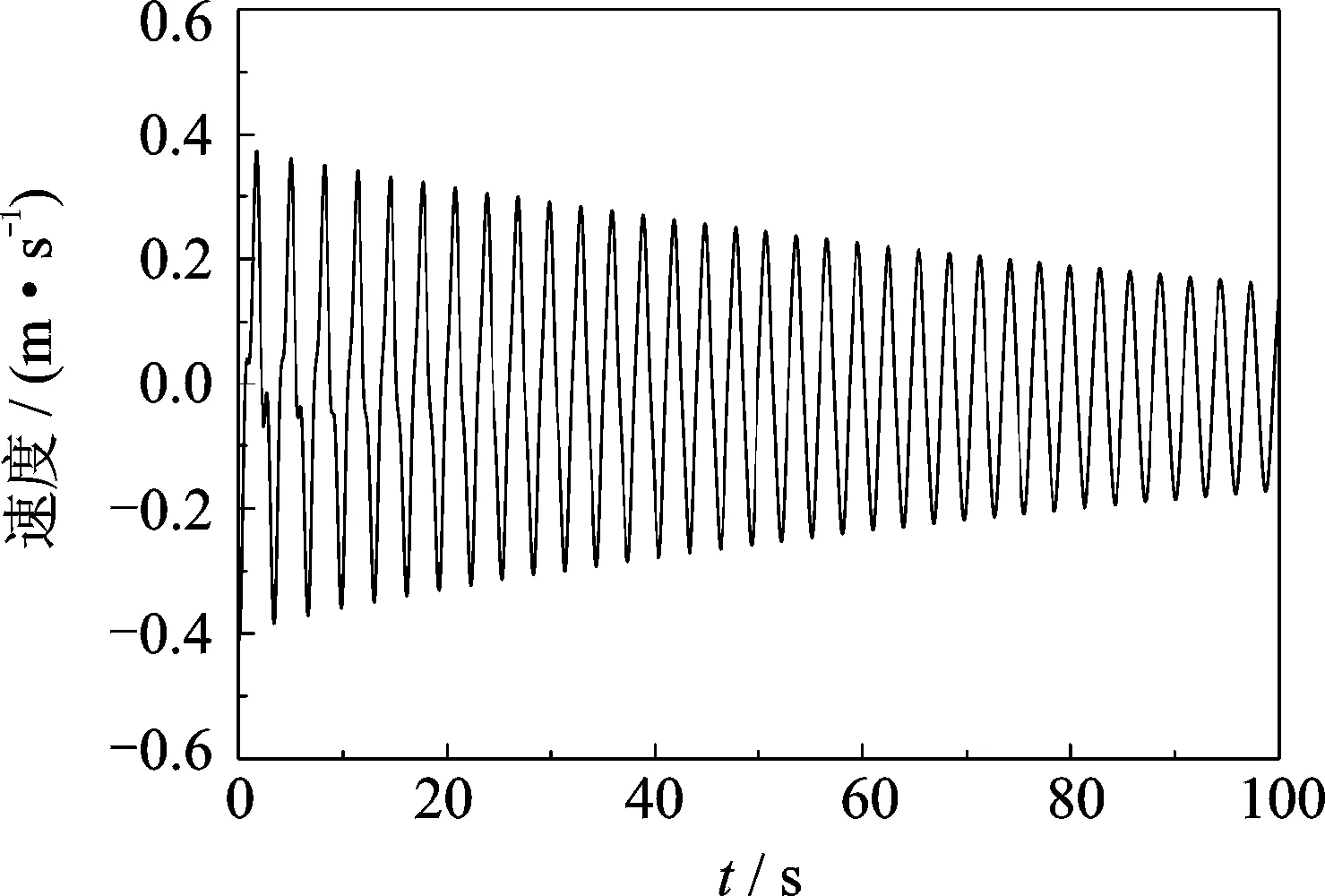
图9 工况5 TMD自由衰减振动速度时间历程曲线Fig.9 The free vibration time histories of the TMD for experimental case 5

4.2 TMD振动频率随振动位移幅值变化规律

由图7～9可知：永磁体作用力的刚度非线性致使摆式TMD频率随时间发生变化，但TMD振动一个完整周期所需的时间仅与振幅有关。由于试验模型具有极低的阻尼比，TMD相邻的两个波峰之间振动衰减很小，为方便研究可近似取相邻两个波峰之间的时间差作为TMD的振动周期。

据此，图10给出了摆式TMD各工况实测振动频率随振动位移幅值变化的对比曲线。由图10可知TMD实测振动频率随振幅的变化规律：对应相同振幅，TMD运动质量块两侧布置相吸永磁体时的频率低于无永磁体工况，且频率随振幅和组数的增加而持续降低；TMD运动质量块两侧布置相斥永磁体时的频率高于无永磁体工况，且频率随振幅和组数的增加而持续增大。理论计算与试验结果均表明：摆式TMD运动质量块两侧布置相吸永磁体时，永磁体作用力产生的附加刚度为负，TMD等效刚度减小，TMD频率降低；摆式TMD运动质量块两侧布置相斥永磁体时，永磁体作用力产生的附加刚度为正，TMD等效刚度增大，TMD频率提高。

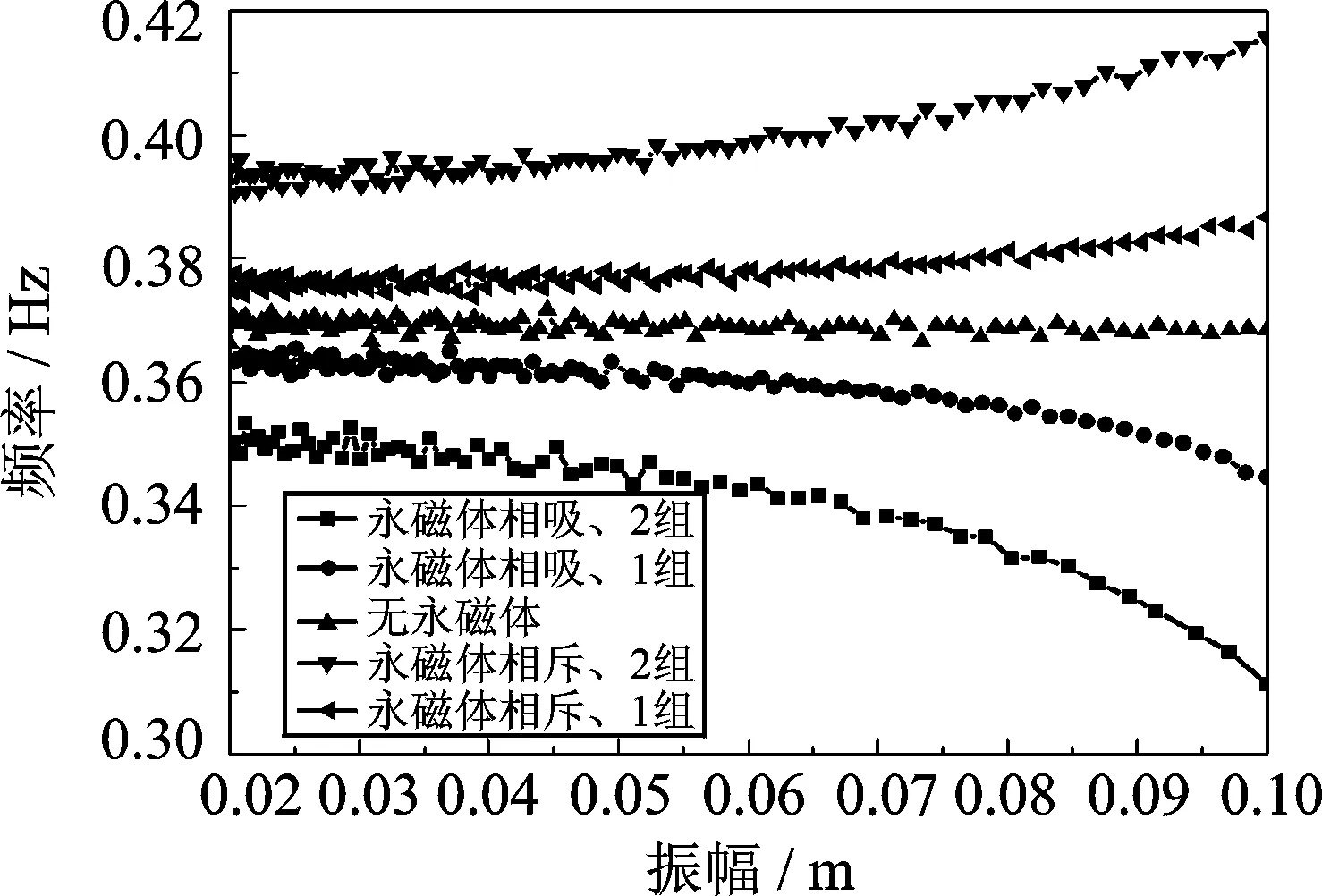
图10 TMD各工况实测振动频率随振幅变化关系Fig.10 Identified vibration frequencies of TMD versus displacement amplitude at each experimental case

与经典摆式TMD不同的是，本文附加永磁体刚度调节装置的摆式TMD振动频率不再保持恒定，而是随运动质量块振动幅值的大小呈现微小的变化，但只要TMD频率偏差控制在5%以内(如本试验模型仅附加1组永磁体时)，就不会显著降低TMD减振效果[20]。

此外，摆式TMD频率设计时以TMD运动质量块处于设计振幅的状态作为目标频率值，导致TMD处于平衡位置或振动幅值超限时，TMD振动频率均将在一定程度上偏离TMD最优设计频率。这既有助于避免TMD长期小幅振动带来的疲劳损伤，也有助于TMD振动幅值超限时的自动限位，TMD耐久性将得到有效改善。

4.3 TMD刚度调节装置刚度理论设计值的确定

表3给出了摆式TMD最大振幅时各工况的振动频率理论值与实验值对比，可以看出频率理论值与实验值相差3.3%～6.7%，且永磁体作用力附加等效刚度实测值均小于相应的理论计算值。误差主要来源：当TMD振幅较大时，永磁体作用力方向与质量块摆动切线方向将出现较大偏移，导致永磁体作用力产生的实际附加刚度下降，而永磁体作用力附加等效刚度理论计算时忽略了这一影响因素必将过高估计附加刚度。

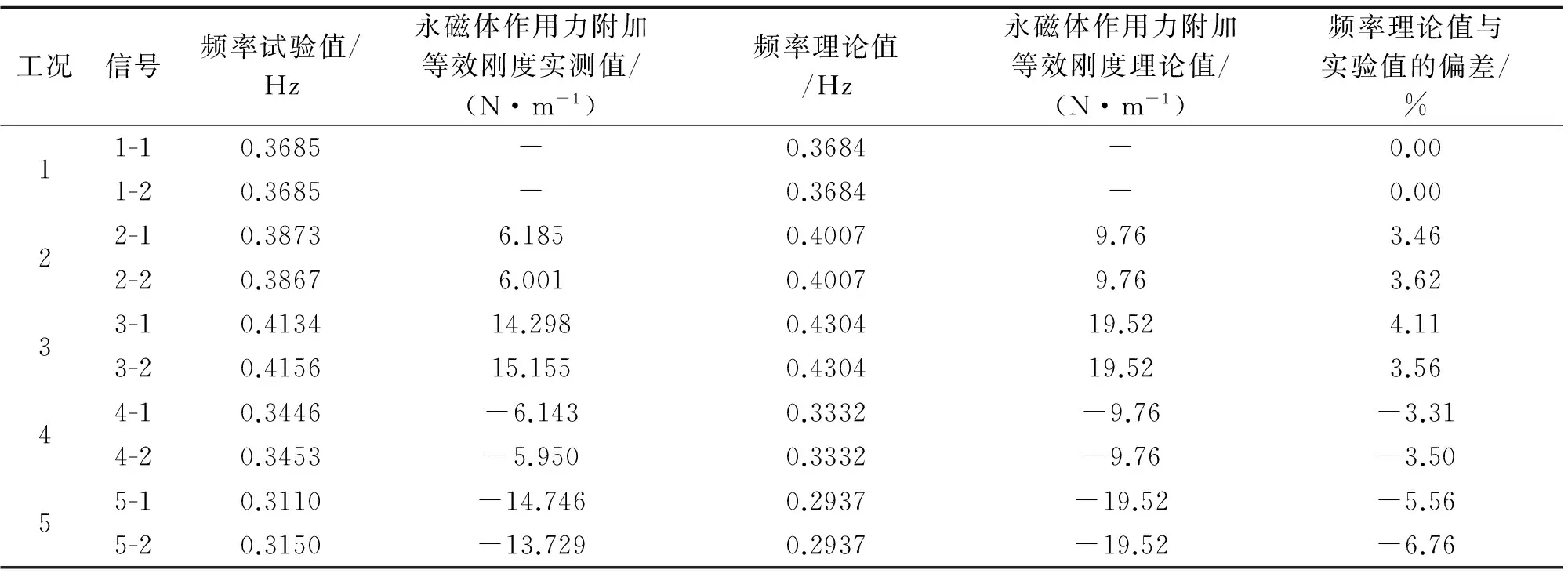
表3 最大振幅时TMD各工况的振动频率理论值与实验值对比

因此，实际设计时建议将式(25)计算的永磁体作用力附加等效刚度理论值进行适当折减后作为永磁体作用力的实际等效刚度，经验证对于本试验模型，该折减系数β取0.74时最大误差仅有1.5%。研究表明：折减系数β主要与永磁体之间的初始间距d0以及摆式TMD设计振幅有关。实际工程应用时，折减系数β可以偏保守的取为0.5，以进一步拓宽TMD频率的调节范围，具体安装调试时可通过调节永磁体之间的初始间距d0或永磁体组数将TMD频率调整到目标状态。

5 结 论

本文提出了一种基于永磁体作用力的摆式TMD频率调节新方法，综合理论分析与模型试验证实了该频率调节方法的可行性，并建立了相应的频率调节设计流程，得到以下结论：

(1)基于永磁体作用力的摆式TMD频率调节方法可以实现TMD频率的双向调节：当摆式TMD运动质量块两侧均布置相吸永磁体时，永磁体产生的附加刚度为负，TMD的等效刚度减小，TMD振动频率降低；当质量块两侧均布置相斥永磁体时，永磁体产生的附加刚度为正，TMD的等效刚度增加，TMD振动频率增大。

(2)附加永磁体刚度调节装置的摆式TMD频率调节设计时，永磁体作用力的附加刚度理论计算值宜适当折减后作为实际等效刚度，该折减系数可偏保守的取为0.5。

(3)附加永磁体刚度调节装置的摆式TMD频率随质量块振动幅值的大小呈现微小的变化，不仅避免了TMD长期小幅振动带来的疲劳损伤，且TMD振幅较大时具有自动限位的趋势与功能，显著提高了摆式TMD的耐久性。

[1] 戴吉, 李春祥. 阻尼器在我国重大工程中的应用与发展[J]. 四川建筑科学研究, 2014, 40(3): 183—187.

Dai Ji, Li Chunxiang. Application and development of dampers to national key engineering [J]. Sichuan Building Science, 2014, 40(3): 183—187.

[2] Gu M, Chen S R, Chang C C. Parametric study on multiple tuned mass dampers for buffeting control of Yangpu Bridge [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(11): 987—1000.

[3] Xing C X, Wang H, Li A Q, et al. Study on wind-induced vibration control of a long-span cable-stayed bridge using TMD-type counterweight [J]. Journal of Bridge Engineering, 19(1): 141—148.

[4] Roffel A J, Narasimhan S, Haskett T. Performance of pendulum tuned mass dampers in reducing the responses of flexible structures [J]. Journal of Structural Engineering, 2013, 139(12): 04013019

[5] 刘勋, 施卫星, 陈希. 单摆式TMD简介及其减振性能分析[J]. 结构工程师, 2012, 28(6): 66—71.

Liu Xun, Shi Weixing, Chen Xi. Introduction and analysis of pendulum-type tuned mass damper [J]. Structural Engineers, 2012, 28(6): 66—71.

[6] 程穆, 汪立军. 阻尼器在上海中心大厦的应用[J]. 上海建设科技, 2014, 3: 26—29.

Cheng Mu, Wang Lijun. Application of dampers to Shanghai Tower [J]. Shanghai Construction Science and Technology, 2014, 3: 26—29.

[7] 宫成, 刘志文, 谢钢, 等. 高墩大跨斜拉桥悬臂施工期风致振动控制[J]. 工程力学, 2015, 32(S1): 122—128.

Gong Cheng, Liu Zhiwen, Xie Gang, et al. Wind induced vibration control of long span cable stayed bridge with high piers during cantilever construction stages [J]. Engineering Mechanics, 2015, 32(S1): 122—128.

[8] 王文熙, 华旭刚, 王修勇, 等. TMD系统在自身参数随机偏离下的减振有效性和可靠性分析[J]. 振动与冲击, 2016, 35(1): 228—234.

Wang Wenxi, Hua Xugang, Wang Xiuyong, et al. Analysis on validity and reliability of TMD system for reducing vibration under random deviation of its own parameters [J]. Journal of Vibration and Shock, 2016, 35(1): 228—234.

[9] Kwok K C S, Samali B. Performance of tuned mass dampers under wind loads [J]. Engineering Structures, 1995, 17(9): 655—667.

[10]Roffel A, Lourenco R, Narasimhan S, et al. Adaptive compensation for detuning in pendulum tuned mass dampers [J]. Journal of Structural Engineering-ASCE, 2011, 137(2): 242—251.

[11]尹学军, 马明, 徐自国, 等. 调谐质量减振器在杭州湾大桥观光塔风振控制中的应用[J]. 特种结构, 2010, 27(3): 23—26.

Yin Xuejun, Ma Ming, Xu Ziguo, et al. Wind-induced vibration control of the sightseeing tower of Hangzhou Bay Sea-crossing Bridge with tuned mass damper [J]. Special Structures, 2010, 27(3): 23—26.

[12]Wang Z H, Chen Z Q, Wang J H. Feasibility study of a large-scale tuned mass damper with eddy current damping mechanism [J]. Earthquake Engineering and Engineering Vibration, 2012, 11(3): 391—401.

[13]Challa V R, Prasad M G, Shi Y, et al. A vibration energy harvesting device with bidirectional resonance frequency tunability [J]. Smart Materials and Structures, 2008, 17, 015035.

[14]Challa V R, Prasad M G, Fisher F T. Towards an autonomous self-tuning vibration energy harvesting device for wireless sensor network applications [J]. Smart Materials and Structures, 2011, 20, 025004.

[15]孙凤, 张明, 孙兴伟, 等. 三自由度等刚度永磁弹簧的力学特性研究[J]. 中国机械工程, 2015, 26(8): 1005—1009.

Sun Feng, Zhang Ming, Sun Xinwei, et al. Study on mechanics characteristics of 3-DOF same-stiffness permanent magnetic spring [J]. China Mechanical Engineering, 2015, 26(8): 1005—1009.

[16]杨红, 赵涵. 稀土永磁弹簧的力学特性研究[J]. 农业机械学报, 2003, 34(1): 111—113, 117.

Yang Hong, Zhao Han. Study on dynamic characters of rare earth permanent magnetic spring[J].Transactions of the Chinese Society for Agricultural Machinery, 2003, 34(1): 111—113, 117.

[17]Zhu Y, Zu J. A magnet-induced buckled-beam piezoelectric generator for wideband vibration-based energy harvesting [J]. Journal of Intelligent Material Systems and Structures, 2014, 25(14): 1890—1901.

[18]Wu H, Tang L H, Yang Y W, et al. Development of a broadband nonlinear two-degree-of-freedom piezoelectric energy harvester [J]. Journal of Intelligent Material Systems and Structures, 2014, 25(14): 1875—1889.

[19]李强, 徐登峰, 范新, 等. 新型永磁隔振器的隔振性能分析与实验研究[J]. 振动与冲击, 2013, 32(13): 6—12.

Li Qiang, Xu Dengfeng, Fan Xin, et al. Analysis and test of vibration isolation performance for a novel permanent magnet vibration isolator [J]. Journal of Vibration and Shock, 2013, 32(13):6—12.

[20]Rana R, Soong T T. Parametric study and simplified design of tuned mass dampers [J]. Engineering Structures, 1998, 20(3): 193—204.

Frequency tuning method in pendulum tuned mass dampers

WANGZhi-hao,GAOHui,ZHANGChuang,LIUFei

(School of Civil Engineering and Communication, North China University of Water Resources and
Electric Power, Zhengzhou 450045, China)

It is difficult to adjust the frequency of large-scale pendulum tuned mass damper (PTMD). To overcome this issue, a new method for frequency tuning in PTMD based on magnetic force is proposed, where the stiffness adjusting device consisted of permanent magnets is attached at the PTMD. The equivalent stiffness of the PTMD can be altered by adjusting the sign and size of the supplemental stiffness generated by magnetic force with permanent magnets. As a result, frequency tuning of PTMD is realized. Differential equation of motion for the combined PTMD and stiffness adjusting device system is established based on Lagrange′s equation. Feasibility of the presented frequency tuning method is well demonstrated, and the effect of vibration frequency on amplitude of the PTMD is qualitatively investigated. Finally, frequency regulation mechanism with magnetic force method is further proved and clarified by model test of a PTMD. Both theoretical and experimental results show that: when attractive force between permanent magnets is applied, the frequency of PTMD will be decreased; while repulsive force between permanent magnets is applied, the frequency of PTMD will be increased. It is also recommended that the supplemental theoretical stiffness generated by magnetic force should be reduced as the actual design value of equivalent stiffness during frequency tuning design of PTMD, and the corresponding reduction factor can be conservatively taken as 0.5.

vibration control; tuned mass damper; frequency tuning; Lagrange′s equation; equivalent stiffness

2015-11-03；

2016-04-16

国家自然科学基金资助项目(51308214)；河南省高等学校青年骨干教师资助计划(2015GGJS-104)；河南省教育厅科学技术研究重点项目(13A560711)；华北水利水电大学青年科技创新人才项目(2014)

TB535+.1; TU352.2

1004-4523(2016)06-1062-08

10.16385/j.cnki.issn.1004-4523.2016.06.016

汪志昊 (1980—)，男，副教授。电话：(0371)65790237；E-mail: wangzhihao916@126.com