PPP模式中公私双方努力水平与收益分配均衡决策研究

游达明 黄睿妮

PPP模式中公私双方努力水平与收益分配均衡决策研究

游达明 黄睿妮

收益分配作为PPP模式中的一个关键决策对项目的成功运行具有重要影响。本文引入Stackelberg博弈模型，分别讨论和比较在集中决策与分散决策下的参与者最优努力水平和最佳收益分配方案，并进一步采用Rubinstein讨价还价博弈模型探究集中式决策下的利润分配。研究发现集中式决策下的努力水平和项目整体利益相对于分散式决策下的努力水平和项目整体利益都有所提高，并且通过对集中式决策下PPP项目的总体利润的合理分配可以实现帕累托改进。

PPP模式 努力水平 收益分配 集中式决策 分散式决策

一、引 言

在过去的几十年里，由于公共预算资金约束和社会公众对于改善和新建基础设施的迫切的需求，政府引进私人投资者进入项目建设得到越来越广泛的关注，于是PPP模式应运而生。PPP模式也即公私合营模式（Public-Private-Partnership），是实现公共项目建设资金来源的新型融资模式，它能够有效解决政府资金紧缺，项目效率低下等问题，从而改进基础设施质量和效率，促进当地经济增长和就业机会，具有很大的应用价值与实践意义。

近年来，国内外学者们对PPP模式下的收益分配问题有了一定的研究。孙慧（2011）对高速公路交通量饱和点与特许经营期时点进行比较分析。Peter Scharle（2002）考虑到私营部门具有的经济属性和社会属性，从四个不同视角将PPP作为博弈问题来分析，建立了一个合理利益均衡的方案。Shapley提出了n个局中人合作的收益分配公式，以其在合作中的“地位”作为收益分配大小的依据，这个“地位”在合作企业中可以理解为对合作的贡献大小、努力程度等（A.Ng,2007）。Viegas（2010）研究了运输项目中PPP合同的收益分摊问题，将再谈判因素、交易成本和合同期限加以了考虑。林旭东等人研究了虚拟企业成员的收益分配方案，并提出了Nash谈判解、Shapley值法、群体重心法以及MCRS法来解决收益分配问题。胡丽基于影响PPP项目的核心利益相关者利益分配的四个影响因素重新修正shapely值，建立使总体利益最大化的利益分配模型，平衡了各方利益。吴书霞等人研究了PPP项目融资中利益相关者的风险与收益的关系协调，考虑风险分摊和资源投入两个因素，提出公平分配的方法。杨从明等在矿产资源开发中采用合作博弈理论，提出利益相关者三方基于Shapely值的收益分配方法，并引入风险承担和投资额进行修正。郑志强等人以鸟巢为案例，借助纳什博弈的分析方法，建立了PPP合作中最优的收益分配模型。徐飞，宋波等运用委托代理理论分析了PPP项目基础设施中公私双方不同阶段的最优努力水平，以及政府奖惩机制对预期收益的影响。卢少华等利用博弈论建立了虚拟企业的利益分配模型，确定出协议中的最优的利益分配系数。叶晓甦（2010）等将资源投入和风险分担等作为激励手段以达到PPP项目利益的公平分配，孙慧（2014）提出了关于不同产权结构下私人部门自利性和公益性努力水平对PPP项目合作效率和政府激励效率的影响。张涵等考虑了公私双方投入和风险分摊情况对初始收益分配比例的影响。

这些研究对PPP模式的深入发展和运行奠定了良好的基础，但是文献中很少涉及关于在分散决策与集中决策角度下的收益方案比较，也较少引入参与方努力水平这一因素，因此有必要探讨在此基础上的收益分配协调机制研究，以及对政府和私人投资者的努力水平造成的影响。本文通过对上述文献的梳理和启发，借鉴Stackelberg（斯坦克尔伯格）动态博弈理念，建立集中决策和分散式决策下的博弈模型，求解出双方最优努力水平并对比研究。再用讨价还价博弈模型获得集中式决策下的最优收益分配比例，由此可以达到激励双方努力的目的，并实现帕累托改进。

二、问题描述和基本假设

假设1政府想要采用PPP模式吸引私人投资者赞助建设一项公共基础设施项目，项目的利益相关者方可能有多个，但本文为了简便起见，只考虑政府与私人投资者两个最主要的利益相关者。项目的建设期投资总额为I，政府投资所占比例为λ，私人投资者占总投资比例为1-λ。

假设2项目的收益主要考虑其带来的直接效益，不考虑间接效益，项目建成后的需求函数与价格以及公私双方的努力水平有关，为了便于讨论，本文根据相关类似文献的描述，设需求函数为线性函数如下：

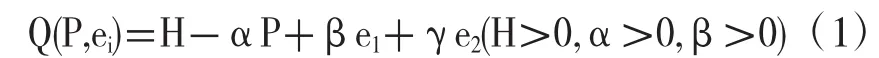
其中H表示项目建成后的潜在确定性需求量，p为价格作为外生变量，为固定值，e1和e2分别表示政府和私人投资者参与项目的努力水平，努力水平表现为诸多方面，比如私人投资者花在技术和服务上的努力程度，政府在税收等方面是否对项目整个经营过程有利等。α，β，γ分别为需求量对价格和双方努力水平的敏感系数，代表着参与双方对需求量的贡献系数。

假设3由于政府和私人投资者存在一种委托代理关系，关于努力成本的衡量，有些学者对其都有假定，相应的合作双方的努力成本分别为：

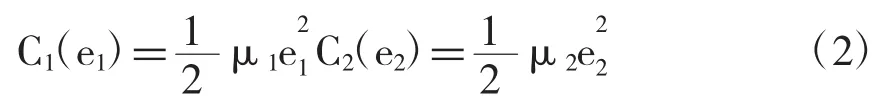
其中μ1＞0，μ2＞0分别为政府和私人投资者的努力成本系数，值越大代表同样的努力水平所带来的成本越多。

假设4假设政府和私人投资者都是理性人，双方根据项目在特许权期内的总收益按线性比例分配，即政府从总收益中获取比例为φ（0＜φ＜1），私人投资者获取的比例则为1-φ。

三、模型构建及求解

1、分散式决策

在分散式决策下，项目的利益相关者双方彼此之间是一个独立的利润中心，追求各自的利益最大化，用上标D表示分散式决策，本文采用Stackelberg博弈模型求出双方最优努力水平和最优收益分配比例。那么在收益共享的契约下，政府和私人投资者的决策目标可以用成本收益函数来表示，将项目的总体收益用价格乘以需求函数表示，根据分散式决策下双方所分配的收益比例与建设期投入成本和努力成本的差额可以得出双方利润最大化的表达函数，也即政府决策目标表示为：

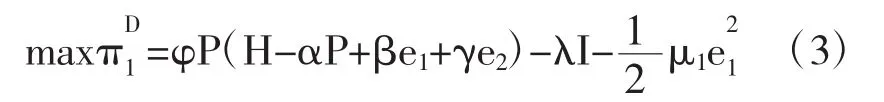
私人投资者的决策目标表示为：

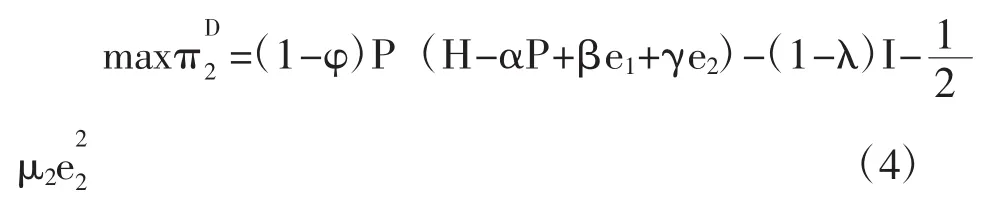
那么分散式决策下，决策模型由如下的规划模型表示：

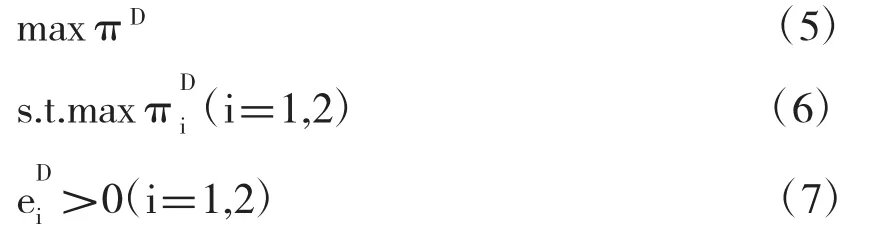
命题1：分散式决策下政府和私人投资者存在最优努力水平，由下式给出：

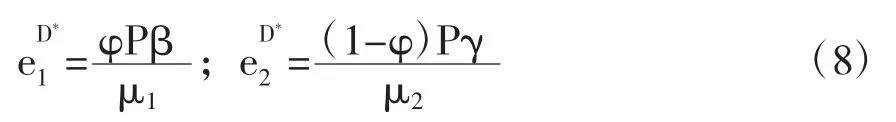
证明：根据逆向分析法分析Stackelberg动态博弈模型，首先考虑博弈的第二个阶段，即政府和私人净收益最大化，将（3）和（4）式分别对努力水平求一阶偏导并令其等于0得到：由此可以推出式（8）成立，证毕。

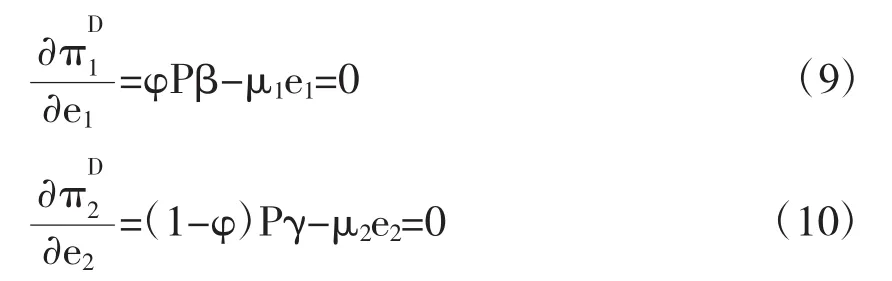
由命题1的结果可以看出在分散决策下的PPP项目中，各参与者的努力水平除了与价格、需求量对努力水平的敏感系数正相关，还与收益分配的比例系数φ和1-φ正相关，同时努力水平与努力成本系数负相关。

下面再考虑博弈的第一个阶段，也就是分配最优收益比例，可以得到命题2：

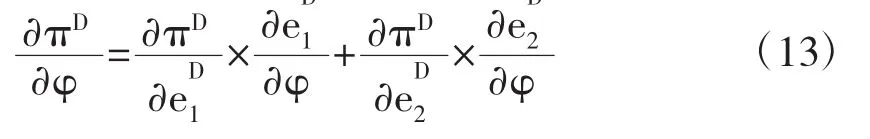
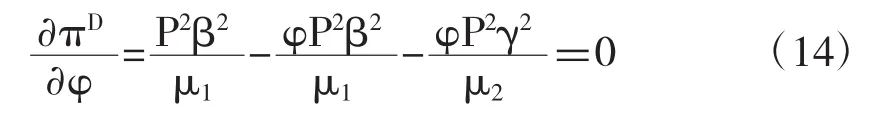
由式（14）可以推得命题4成立，证毕。

将求得的φ*和1-φ*分别对γ和β求导，可，再将φ*和1-φ*对μ1，μ2各自求导，可以得到从这些结果可以推出下面结论：分散式决策下的收益分配比例与项目参与双方自身对需求量的贡献系数（敏感系数）正相关，与自身的努力成本系数负相关，与合作方的努力成本系数正相关。即当自身贡献系数越大，所得到的收益分配比例越大，自身努力成本系数越高，所得分配系数越小，合作方努力成本系数越大，所得收益分配系数越大。

命题3：将式（8）代入（1）、（3）、（4）可以得到在分散决策下政府和私人投资者各自的最优利润以及整体最优整体利润：

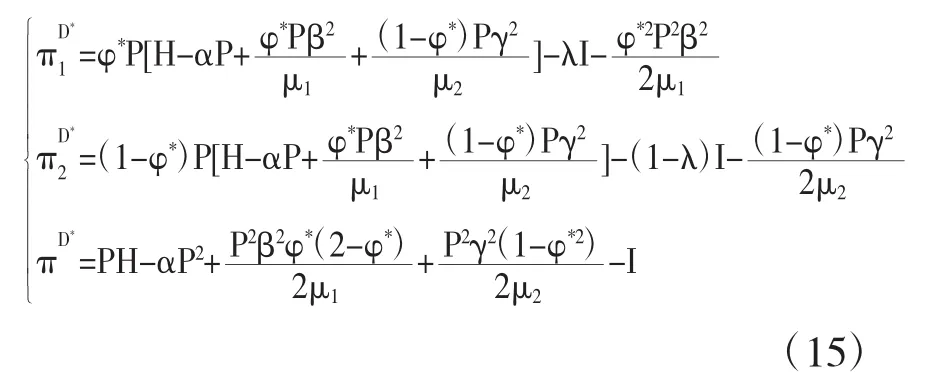
从（15）式中的整体利润来看,在总利润和分配比例的关系中，通过对上面求出的最优结果进一步分析，可以发现当φ＝φ*时，＝0；当0＜φ＜φ*时，＞0，这表明当分配比例处于这个范围时，随着政府的收益分配比例越大，整个PPP项目的总的利润也会变大，因此可以使得分配比例满足0＜φ＜φ*，来保证PPP项目的收益，因为如果给予的政府权利过小，那么政府和社会公众对私人投资者的约束监管能力就过小，容易造成私人投资者道德风险；当φ*＜φ＜1时，＜0，这表明随着政府和社会公众的收益分配比例变大，PPP项目的整体利润随之减小，因此当分配比例系数大于φ*时，会对PPP项目的整体利润造成负面作用，因为在采用PPP模式的公共基础设施项目中，如果给予政府的权利过大，那么私人投资者就失去了参与的积极性，造成懈怠和投资建设兴致不高的状况，市场化缺失从而负面影响变大，这也是我国目前实行PPP模式建设一些基础设施项目所遇到的一个难题，即政府过度控制和控股。

在PPP项目的整体利润与私人投资者的努力水平关系中，经过进一步分析可以得到当时，＜0，这表明当私人投资者的努力水平超过一定程度时，PPP项目的整体利润随着私人投资者的以得到努力水平增加而减小；当＞0，说明当私人投资者的努力水平控制在一定范围时，PPP项目的整体利润随着私人投资者努力水平的增加而增加。同样的，政府的努力水平对于PPP项目的整体利润之间的影响关系也是如此。这表明在采用PPP模式的项目中，政府、私人投资者的努力水平必须控制在一定的区间之内，然后由此加强努力来提高总利润，而并不是一味的越努力越好，相反过于的努力水平会适得其反。

2、集中式决策

在集中式决策下，政府和私人投资者作为一个利益中心，而不是对立面，考虑的是整体净收益最大化，那么集中决策时双方的决策模型可以表示为净收益最大化，本文用上标C表示集中式决策即：

将式（1）、（2）代入（16）得到：

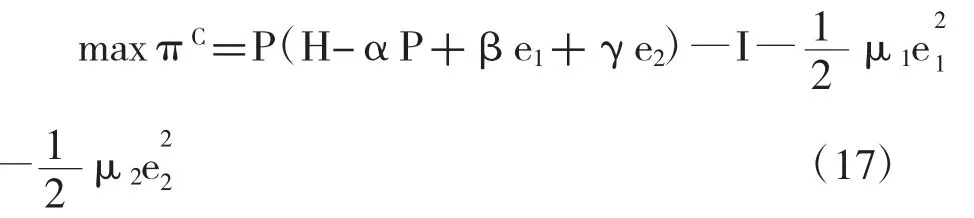
命题4：集中式决策下政府和私人投资者最优努力水平均衡策略满足：

证明：利用一阶导数等于0的求极值方法，将（17）式分别对e1，e2求偏导得到

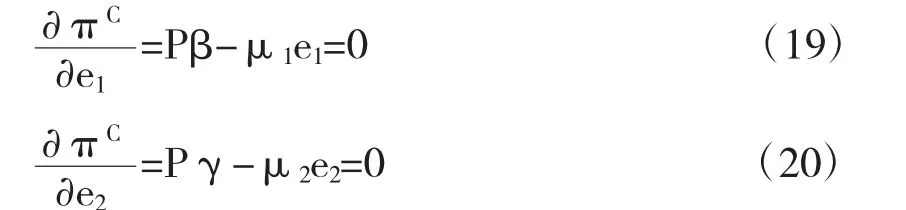
由（19）、（20）式可推出（18）式成立，证毕。

命题4表明，政府和私人投资者的PPP项目最优努力水平与价格、需求量对努力水平的敏感系数正相关，与努力成本系数负相关。这说明当努力成本系数越高时，双方会倾向于降低自身的努力水平，以维持努力成本不会过高；当价格越高，PPP项目的直接运营收益也就越高，也就能够激励他们提高自身努力水平，对项目建设运营提供更好的维护和服务；同样，当敏感系数越高，PPP项目的公众收益群体也就愈倾向于使用，需求量增多，自然收益也提高，从而也能促进努力水平提高。

命题5：将（18）式代入（17）可得到集中式决策下政府和私人投资者的整体利润如下：

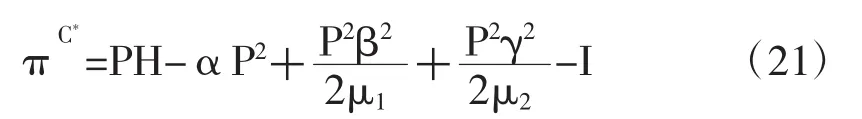
将命题1与命题4，命题3与命题5比较，由于φ*是大于0小于1的数，那么有

通过比较集中决策与分散式决策下的努力水平与整体净收益发现，集中决策下政府和私人投资者的努力水平比分散式决策下的努力水平高，且社会总体净收益也较之有所增加，这说明个体决策者理性并不是最佳选择，这体现出非合作博弈的局限性，而在PPP项目中这种集体理性行为更能得到普遍的运用，从总体理性角度出发使得项目的总体利益朝着最大化的目标奋斗，这种集中决策的合作行为才能进一步实现帕累托最优化。

四、利润分配设计

根据上述分析可以知道如果在集中式决策下政府和私人投资者双方能够合理的分配利润，那么将促使两者的利润均高于分散式决策下的利润，并且能够激励双方提高努力水平，所以怎样确定分配利润比例将关系重大，用θ表示政府分配的利润比例，要使得集中式决策下政府和私人投资者分享的利润均实现帕累托优化，必须满足：

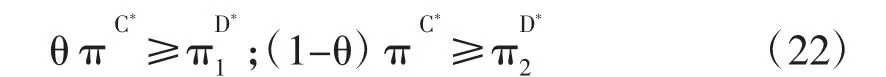
关于上式中一个重要的谈判系数σ，它一般理解为讨价还价的一种时间成本，类似于随着时间的拖延蛋糕不断地缩小，每一轮讨价还价总成本与剩余蛋糕成一定比例，在谈判过程中双方损耗的时间、可能的利息损失、错过其他投资机会的成本等。

通过将x*对σ1，σ2分别求导，发现＞0，＜0，由此可知参与双方的最终均衡解与自身的贴现因子正相关，与对方的贴现因子负相关，因为贴现因子越大，表示自身的耐心程度越高，较能经得起谈判拖久的时间成本，因此在谈判中占有优势。

命题6：此时可以得到在集中式决策下，当θ∈[θmin,θmax]时的最优利润分配比例为：

命题7：集中式决策下，政府和私人投资者所得到的最优利润分别为：

从命题7可以看出这实际上是一个收益的再分配过程，即通过对参与方努力后所增加的收益进行再分配，可以实现集中式决策下政府和私人投资者的利润均高于分散式决策下两者所得利润，所分得利润与自身的贴现因子正相关。

五、数值仿真分析

表1 努力成本系数对公私方博弈均衡策略的影响

由表1可以看出，当参数值相同时，集中式决策的努力水平普遍要高于分散式决策下的努力水平，政府和私人投资者各自的利润在集中式决策下均大于分散式决策，项目整体利润更是如此，由此可以说明集中式决策下的合理分配利润可以实现帕累托最优。当分散式决策下政府的努力成本系数μ1不变

假设某项目要采用PPP模式运作，政府要吸引私人投资者进行投资,政府占有绝对控制权，所占投资比例为0.6，私人投资者投资比例为0.4，也即λ＝0.6，为了直观表现和计算，将其他基础参数假设为：H＝4000，I＝1000，P＝6，α＝10，β＝10，γ＝15，σ1＝0.6，σ2＝0.4，通过对μ1，μ2取不同值，可以求得相关决策变量在两种决策情形下的均衡值，如下表1所示：时，随着私人投资者的努力成本系数μ2越来越大直至高于μ1，收益配比φ*越来越大，两者的努力水平越来越达到相当水平，且两者的努力水平随着彼此互相都有变动，这说明努力水平还受到φ*的影响，反之当μ2不变，μ1变大时，收益配比φ*越来越小。而在集中式决策下，当μ1不变，μ2值递增时，政府的努力水平是不变的，私人投资者努力水平随之变小，反之亦然，而利润分配比例随着μ2增加而增加，随着μ1的增加而减少。

六、结束语

本文在已有文献的基础上，假定项目的直接收益可以由定价与需求量来直接计算，并将参与者的努力水平纳入模型研究，综合考虑政府和私人投资者两个主要PPP项目利益相关者在收益分配中的决策与协调机制，分别计算出在集中式决策与分散式决策下两者的努力水平与项目的整体利润的最优形式，并采用讨价还价博弈模型确定集中式决策下的利润分配比例。研究结果表明①集中式决策下政府和私人投资者的最优努力水平分别与价格、需求量对努力水平的敏感系数正相关，与努力成本系数负相关。②分散式决策下参与者的努力水平除了与价格、需求量对努力水平的敏感系数正相关，还与各自收益分配的比例系数正相关，而收益分配比例又与参与方自身的贡献系数正相关，与各自的努力成本系数负相关。③当政府的收益分配比例在一定范围内时，项目整体利润与之正相关，反之负相关；同样的当私人投资者的努力水平控制在一定范围内时，项目整体利润随之增大而增大，反之增大而减小。④集中决策下政府和私人投资者的努力水平比分散式决策下的努力水平高，且总体利润也较之有所增加。⑤通过合理的分配集中式决策下的净收益可以实现帕累托改进，以此可以激励双方达到理性合作的目的。

通过上述的分析可以得出一些有效政策建议，首先政府需要时刻保证自己的主要职责，加强对私人投资者的管控能力，避免太过市场化，并且需要发挥宏观政策的作用，保持一定的领导力，建立专业有效的监管机制并落实，控制管理运营风险，通过宏微观政策的实施才能确保收益分配比例合理化、最优化。其次在政府吸引私人投资者加入PPP模式项目建设中时，可以对私人投资者适当的放权，有的放矢才能更好的对私人投资者和PPP项目进行监管。在制定激励措施刺激合作方提高自身努力水平的同时还需要严格管控各方努力水平的正常范围，这是保证项目整体利润的关键，杜绝政府过度的干预项目。当然本文的研究是基于一系列的相关假设，具有局限性，今后研究中可以纳入潜在的价值或损失这样的间接损益。

［1］孙慧，范志清，石烨.PPP模式下高速公路项目最优股权结构研究.管理工程学报.2011.25（01）154-157

［2］Scharle Peter.Public-private partnership (PPP)as a social game.Innovation:the European Journal of Social Science.2002.15(3)227-252

［3］A.Ng,Martin Loosemore.Risk allocation in the private provision of public infrastructure.International Journal of Project Management.2007:66-76

［4］Viegas J M,Questioning the need for full amortization in PPP contracts for transport infrastructure.Research in Transportation Economic.2010(30)139-144

［5］林旭东.虚拟企业合作及契约研究.管理工程学报. 2001.15（1）26-28

［6］胡丽，张卫国，叶晓甦.基于shapely修正的PPP项目利益分配模型研究.管理工程学报.2011.25（02）149-154

［7］吴书霞.我国PPP项目合作中的利益关系及分配方式研究.科学进步与对策.2010.27（19）36-38

［8］杨从明，朱海彬.基于Shapely值法的矿产资源开发利益相关者利益分配博弈分析.地球与环境.2014.42（03）424-428

［9］郑志强，陶长琪.大型体育设施供给PPP模式的合作博弈分析.体育科学.2011.31（5）27-32

［10］徐飞，宋波.公私合作制（PPP）项目的政府动态激励与监督机制.中国管理科学.2010.18（03）166-172

［11］卢少华.虚拟企业联盟的利益分配博弈.管理工程学报, 2004,18（03）65-68

［12］叶晓甦，吴书霞，单雪芹.我国PPP项目合作中的利益关系及分配方式研究.科技进步与对策.2010（19）36-39

［13］孙慧，赖毅.PPP限价房项目中合作效率与政府激励效率博弈研究.工程管理学报.2014.28（05）110-114

［14］张涵，王卓甫.交通量可观测条件下PPP公路项目收益分配.工程管理学报.2015.29（01）72-75

［15］高颖.PPP项目运营期间需求量下降情形下的补偿机制研究.管理工程学报.2015.29（02）93-102

［16］张延龙.销售努力和价格影响需求时的供应链协调研究.软科学，2012，26（01）132-136

［17］李林，刘志华，章昆昌.参与地位非对称条件下PPP项目风险分配的博弈模型.系统工程理论与实践.2013. 33（08）1941-1948

［18］张维迎.博弈论与信息经济学.上海：上海人民出版社. 1996

Research on Equilibrium of Effort and Income Distribution Decisions between Public and Private Partner in PPP

YOU Da-ming,HUANG Rui-ni
School of Business,Central South University,Changsha 410083 Collaborative Innovation Center of Resource-conserving&Environment-friendly Society and Ecological Civilization,Central South University,Changsha 410083

Income distribution,as a key decision of PPP mode,exerts a significant impact on the successful operation of a project.This paper introduces Stackelberg game model to analyze and compare the optimal effort level and income distribution of participants under two different decision situations including decentralized and centralized decision.Furthermore,using Rubinstein bargaining model,it discusses the profits distribution under centralized decision.The results show that the effort level and overall interests of the project under centralized decision areimproved with respectto thesituation under decentralized decision.Besides,reasonable profit allocation of the centralized decision could realize“Pareto improvements”.

Public-private Partnership,Effort,Income Distribution,Centralized Decision,Decentralized Decision

F294

A

教育部哲学社会科学研究重大课题攻关项目（13JZD0016）；国家自然科学基金面上项目（71172100）；国家软科学研究计划项目（2014GXS4D135）

游达明，男，中南大学商学院教授、博士生导师，研究方向：技术创新与管理、投融资决策和企业战略管理

黄睿妮，女，中南大学商学院硕士，研究方向：投融资决策、生态技术创新；湖南长沙，410083