基于关系层次性的局部社团探测方法

邹斌

（安徽广播电视大学，安徽 合肥 230022）

基于关系层次性的局部社团探测方法

邹斌

（安徽广播电视大学，安徽 合肥 230022）

挖掘复杂网络的社团结构对研究复杂系统具有重要的理论和实践意义，局部社团探测是其主要挑战之一。目前对局部社团探测方法的研究甚少，且大多算法精确度过低。对此从关系的层次性考虑，通过节点的相对相似性和一个参数α定义了朋友和最好朋友的概念。给出三个假设，并在此基础上设计了基于关系层次性的局部社团探测算法（HR）。实验表明，HR要优于当前同类算法。最后经分析，发现参数α的最优值与网络的平均相对相似度成正相关。

社团结构；局部社团探测；朋友；最好朋友

引言

社团结构普遍存在于社会网、信息网、生物网等，网络的社团结构对于理解网络的组织结构和其所代表的功能特性有着重要意义。到目前为止，人们提出了很多经典的社团探测方法。2002年Girvan和Newman提出了“边界数”的概念①Grivan M,Newan M E J,"Community Structure Insocial and Biological Networks",Proc of National Academy of Science，Vol.99,No.12,2002,pp.7821-7826.，边界数定义为网络中通过某条边的两点间最短路径的条数。社团内点之间连接紧密，社团内相互连接的路径较多，任意两点之间的最短路径会比较均匀地经过各条边，所以社团内部的边界数较低。而不同社团之间由于连接较少，导致跨社团的边成为连接不同社团的点对之间的必经之路，所以这类边的边界数一般比较高。边界数高的边具有明显的“桥梁效应”。GN算法就是通过删除边界数较高的边完成社团的划分过程的；Newman随后又提出了一种快速的模块度局部最优化算法②Newan M E J,"Fast Algorithm for Detecting Community Structure in Networks",phys Rew E,Vol.69,No. 6,2004,066133.，局部最优解是可以找到的。首先所有节点都被看成单个社团，在每次迭代过程中选择其中一对社团进行合并，这对社团的合并可以带来模块度增益的最大化，迭代过程一直进行，直到模块度达到极大值时停止，Blonde③Blodel,Vincent D.,et al,"Fast Unfolding of Communities inLarge Networks",Statistical Mechanics:Theory and Experiment,No.10,2008,PI0008.也提出了类似的算法。其它的社团探测算法还有很多，如基于谱分析的社团探测算法④Capocci A,Servedio V D P,Caldarelli G,et al,"Detecting Community in Large Networks",Physica A: Statistical Mechanics and Its Applications,Vol.152,No.2-4,2005,pp.669-676.和标签传播算法⑤Raghavan U N,Albert R,Kumara S,"Near Linear Time Algorithm to Detect Community Structure in largeacale Networks",Phys ReV E,Vol.76,No.3,2007,036106.等。

上面所述的都是全局的社团探测算法。但是在现实中，很难获取网络的全局信息，而且许多情况下只需要知道某些节点所在的社团信息，并不需要知道整个网络的情况，所以局部社团探测算法的设计是非常有意义的。局部社团探测算法的研究不多，这些算法主要都是一些扩张算法。如文献①Clauset A,"Finding Local Community Structure in Networks",Physical Review E,Vol.72,No.2,2005,026132.提出了一种基于R值的局部社团探测算法，该算法首先定义一个局部模块度R，然后应用贪婪算法的思想，迭代添加使R值增加最大的邻居节点，直到社团达到预定的规模，该算法最大的缺点是事先需要知道社团的大小。其它的还有类似的基于随机种子扩张的LFM算法②Luo F,Wang J Z,"Promislow E.Exploring Local CommunityStructures in Large Networks",Web Intelligence and Agent Systems,Vol.6,No.4,2008,pp.387-400.，基于模块度M的LMD算法③Chen Q,Wu T T,Fang M,"Detecting Local Community Structures in Complex Networks Based on LocalDegree Central Nodes",Physica A:Statistical Mechanics and Its Applications,Vol.392,No.3,2013,pp.529-537.等。

本文考虑关系的层次性，通过节点的相对相似性和一个参数α定义了朋友和最好朋友的概念。在现实中，如果我的最好朋友在一个朋友圈，我基本上也属于这个朋友圈；如果我和某个人互为朋友，则我们在一个朋友圈的可能性就很大；还有如果我的很多朋友都在这个朋友圈，我很难不在这个圈子内。基于这些现象提出了三个假设，然后可以得到任意一个节点通过扩张得到的社团。实验表明，本文的算法要优于当前同类算法。最后经分析，还发现一个有趣的现象：参数α的最优值与网络的平均相对相似度成正相关。

1相关定义

在现实生活中可能认识的人很多，不是每个人都能称作为朋友，而朋友又有好与普通之分。如图1，所有节点都是A所认识的人，而能称作朋友的有4个，4个里面还有1个最好朋友。可以假设节点A和自己的最好朋友（唯一）一定在一个社团（很难想象你和你的唯一兄弟身处两个社团，这违背社团的定义）；节点A的普通朋友如果绝大多数在一个社团内，则A也一定在这个社团；另外，还可以认为如果两个节点互为朋友，则这两个节点在一个社团内（在网络中两个节点互为朋友，则说明他们可能有着某种相似结构，且互相紧密相连，这与社团内部紧密相连不谋而合）。根据这些假设，可以用扩张的算法得到网络任意一个节点所在的社团。在这里首先给出节点的朋友与最好朋友的定义。

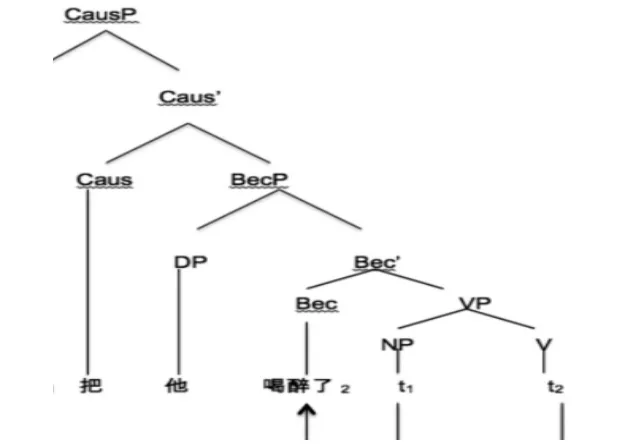
图1 节点A的关系层次图

定义G(V,E)为一个无向网络，其中V为节点集合，E为边集合。Γ(v)为节点v所有邻居的集合，为集合元素的个数。于是网络中任意两个有连边的节点x,y的相似关系的强弱可以用共同邻居的个数（共同邻居越多相似性越大）来衡量：

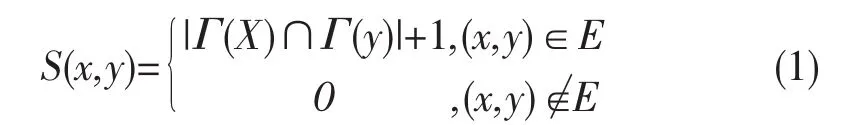
由上式可以看出两个节点只要有连边就有关系。接着给出节点的最大相似性指标：

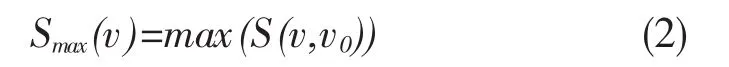
因此节点v和其所有邻居相对相似度可以定义为：

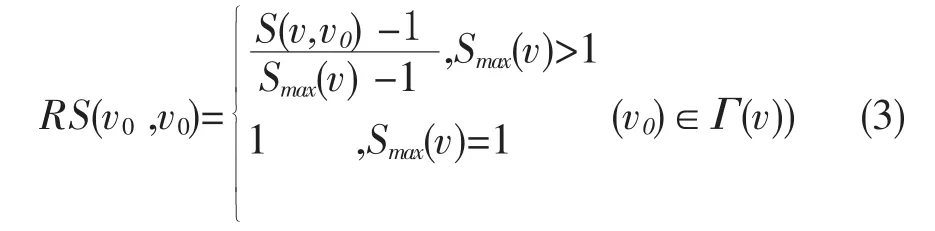
由上式可以看出：S(x,y)=S(y,x)，但是RS(v,v0)≠RS (v0,v)。显然，根据节点v和其所有邻居相对相似度，再给定一个参数α，可以给出节点v在参数α下的所有朋友集合fα(v)。若，v0∈fα(v),则须满足：

由上式可以看出：f0(v)是节点v的所有邻居的集合；f1(v)为和节点v最相似节点集合。于是可以给出节点v的最好朋友集合：

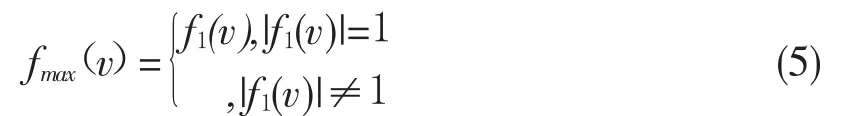
由上式可以看出如果节点v最相似的邻居唯一则有最好朋友，否则没有最好朋友。

2 HR算法

2.1 算法设计与步骤

根据上述定义，可以给出前文提到的三个假设的规范表达，设G为某个节点通过扩张得到的社团。

假设1：若v∈G，则fmax(v)∈G,；若fmax(v)∈G，则v∈G（节点v和自己的最好朋友在一个社团）；

假设2：若v1fα(v2)，v2∈fα(v1),v1∈G则v2∈G（节点v1,v2互为朋友，则两个节点同属一个社团）；

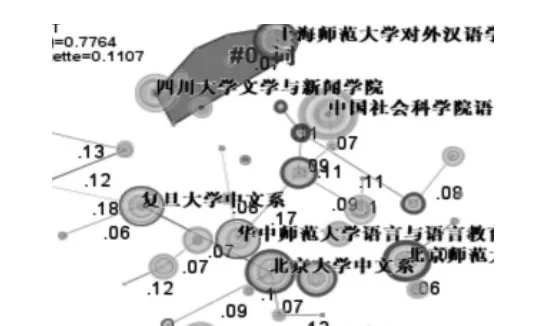
图2 实例网络

根据上述三个假设可以找到任意一个节点所在的社团。如表1是图2所有节点的信息，其中a= 0.6。现在要寻找节点1所在的社团。

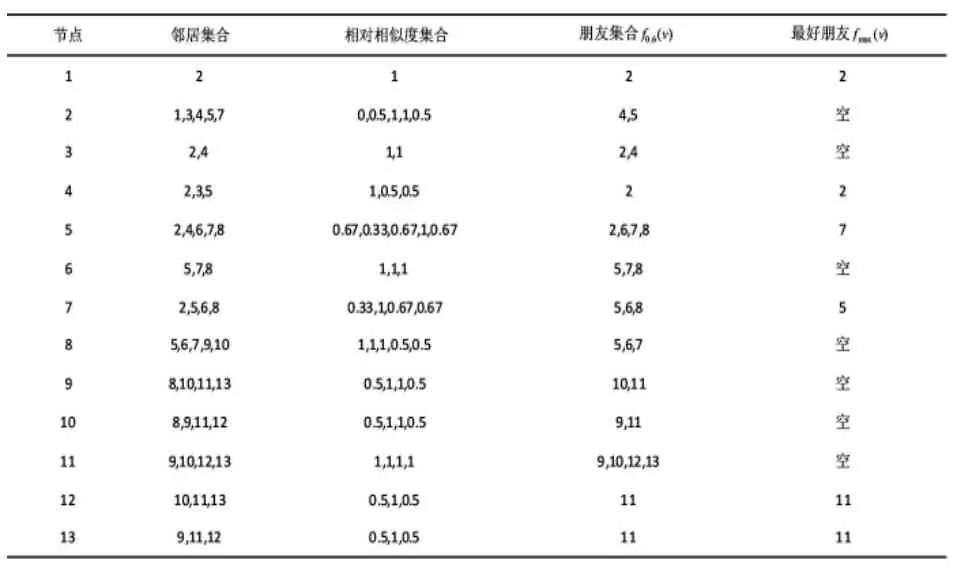
表1 图2中每个节点的属性信息（邻居集合和相对相似度集合一一对应）

首先，节点2是节点1的最好朋友，则节点2在这个社团（假设1）；接着节点2又是节点4的最好朋友，所以节点4并入该社团（假设1）；节点3的朋友是节点2和4，它们都在社团内，所以节点3也属于该社团（假设3）；节点5和节点2互为朋友，所以节点5在社团内（假设2）；又节点6、7、8分别和节点5互为朋友，所以它们也是社团的一部分（假设2）。这时，由节点1扩张的社团为：1、2、3、4、5、6、7、8。又社团的所有邻居与社团内部节点都不满足三个假设条件，所以扩张结束。得到的结果可以看到与实际情况吻合。下面给出基于多层次相似关系的局部社团探测方法（HR）的步骤。

设CS(v)是由节点v扩展得到的社团，ACS为准社团，ACS中的元素会逐个移动到CS中，FS为朋友集合。则给定一个节点v0，由v0扩张得到社团CSv0的步骤为：

算法1：

初始化：CS=O，ACS=｛v0｝，FS=。

Step1：从ACS中取出一个元素v放入CS这中，即，ACS=ACS-v,CS=CS∪v。

Step2：讨论节点v：ACS=ACS∪(fmax(v)-CS)；假设1）。

Step3：讨论节点v的邻居，对任意v1∈Γ(v)且v1∈(ACS∪CS):

（1）若fmax(v1)=v，则ACS=ACS∪(v1-CS（)假设1）。

（2）若v∈fα(v1)，v1∈fα(v),则ACS=ACS∪(v1-CS)（假设2）。

（3）若v∈fα(v1)，则FS=FS∪v（1存在朋友在社团内的节点）。

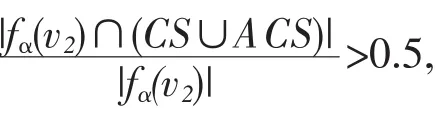
Step5：转到step4，直到FS不变。

2.2 算法分析与改进

该算法是经过对节点的邻居和节点的关系分析，然后一步步扩张得到该节点的所在的社团。但是，节点会不会出现扩张不出去的状况呢？如图2和表1，若想找节点3所在的社团，但是节点3没有最好朋友，也没有节点以节点3为最好朋友，甚至没有节点和节点3互为朋友。所以，以节点3为初始点，得到的社团就是节点3本身。这和实际情况不相符，所以需要对算法进行改进。

遇到上述情况，只需考虑该节点的邻居节点扩张情况，如果节点的邻居扩充得到的社团包含这个节点，则该社团就是这个节点所在的社团，否则可以说明该节点为孤立点。如图2，节点3的邻居2和4扩张得到的社团都是：

1、2、3、4、5、6、7、8，所以可以认为节点3所在的社团为：1、2、3、4、5、6、7、8。

这里可以给定一个参数β，用来控制最小社团大小。则由v0扩张得到社团CS(v0)的步骤为：

算法2：

Step1：通过算法1得到CS(v0)，若CS(v0)＞β，转step3，否则转step2。

Step2：对于任意v∈Γ(CS(v0))，由算法1计算CS(v)。直到存在v使得CS(v0)∈CS(v)，则CS(v0)=CS (v)。如果对任意v，CS(v0)∈CS(v)都成立，则转step3。

Step3:输出Γ(CS(v0))。

这里Γ(CS(v0))为CS(v0).中所有节点的邻居集合。参数β的取值默认为2，因为三个节点组成一个社团是很有可能存在的，实验也验证当β取大于2时，完全是增加计算量，基本不会改变节点扩张结果。

2.3 复杂度分析

设由节点v扩张得到的社团CS(v)的规模是n1，社团的边数为m1（与社团内部所有节点相连的边个数），该社团内部的平均度为＜k＞。算法主要有两个部分：相似度计算和算法扩张。因为节点的相似度基于共同邻居，所以时间复杂度大致为：m1＜k＞2。而扩张过程只针对其邻居，所以算法的复杂度大概为：n1＜k＞。综上所述HR算法的时间复杂度约为：m1＜k＞2+n1＜k＞。可以看出本文HR算法时间复杂度不高，接近线性。

3 数值实验

本文将HR算法分别与Clauset-R①Clauset A,"Finding Local Community Structure in Networks",Physical ReviewE,Vol.72.No.2,2005, 026132.、LFM②Luo F,Wang J Z,"Promislow E.Exploring Local CommunityStructures in Large Networks",Web Intelligence and Agent Systems,Vol.6,No.4,2008,pp.387-400.、LMD③Chen Q,Wu T T,"Fang M.Detecting Local Community Structures in Complex Networks Based on LocalDegree Central Nodes",Physica A:Statistical Mechanics and Its Applications,Vol.329,No.3,2013,pp.pp.529-537.等局部社团挖掘算法进行比较。为了方便，采用最常见的几种网络数据进行测试。其中包括Zachary空手道俱乐部成员关系网（Karate）④Zachary W W,"An Information Flow model for Conflict and Fission in Small Groups".Journal of Anthropological Research,Vol.33,No.4,1977,pp.452-473.、宽吻海豚网络(dolphins)⑤Lusseau D,Schneider K,Boisseau O J,Haase P,Slooten E,Dawson S M,"The Bottlenose Dolphin Community of Doubtful Sound Features a Large Proportion of Long-lasting Associations",Behavioral Ecology and Sociobiology,Vol.54,No.4,2003,pp.396-405.、美国政治书籍网络(polbooks)⑥Newman M E J,"Modularity and Community Structure in Networks",Proceedings of National Academy of Sciences of the United States of America,Vol.103,No.23,2006,pp.8577-8582.和美国大学橄榄球联赛网络(football)⑧Grivan M,Newan M E J."Community Structure Insocial and Biological Networks",Proc of National A－cademy of Science,Vol.99,No.12,2002,pp.7821-7826.四个网络。

3.1 算法结果评价指标

在这里应用三个指标来衡量算法的优越：准确率P、召回率R和综合评级指标F⑧Strehl A,Ghosh J,"Cluster Ensembles-A Knowledge Reuse Framework for Combining Multiple Partitions", Journal on Machine Learning Research,No.3,2002,pp.583-61.。

（1）准确率

准确率反映了划分结果中正确节点数量占划分结果规模的比例。其定义如下：

（2）召回率

召回率反映了真实社团中被正确划分出的节点的比例。其定义如下：

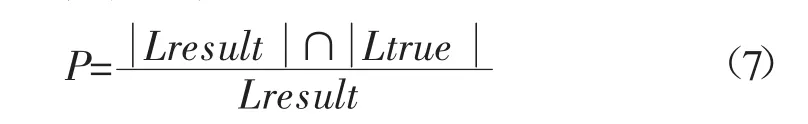
（3）综合评价指标

P值和R值只能反映算法的某一方面。P值高说明划分结果中正确的节点的数量占划分结果规模的比例较大，但是却不能判断是否过划分，比如极端的情况下只划分出社团的一个节点，其P值达到最大为1。R值高说明真实社团中更多的节点被划分出来，但是却不能判断是否欠分割，比如极端情况下将整个网络划分为一个社团，其R值最大为1。因此单从P值和R值无法判断一个算法的性能，所以下面给出一个更合理指标，即综合评价指标F：

3.2 实验结果

应用HR算法求得每个节点所在的社团，分别计算其P、R、F指标，然后平均得到最终HR算法的三个评价指标结果见表2。表中Clauset-R、LFM和LMD算法结果来源于文献⑨Chen Q,Wu T T,"Fang M.Detecting Local Community Structures in Complex Networks Based on LocalDegree Central Nodes",Physica A:Statistical Mechanics and Its Applications,Vol.329,No.3,2013,pp.529-537.。其中HR算法中的参数a=0.6。结果表明HR算法明显优于其它三种算法。

3.3 参数分析

很明显，参数α的取值不同，得到结果也不同。如图3可以看出，随着α增大，HR算法的P指标逐渐增加，R指标逐渐减小。这是因为，当α很小的时候，节点和他的邻居更容易成为朋友，所以由假设2（两个节点互为好友在同一个社团）可知，整个网络很难被分开，是欠划分的状况，所以R值很大，P值很小。随着增大，社团被划分的越来越细，所以P值逐渐增加，R值逐渐减少，当α很大的时候会出现过划分的情况。

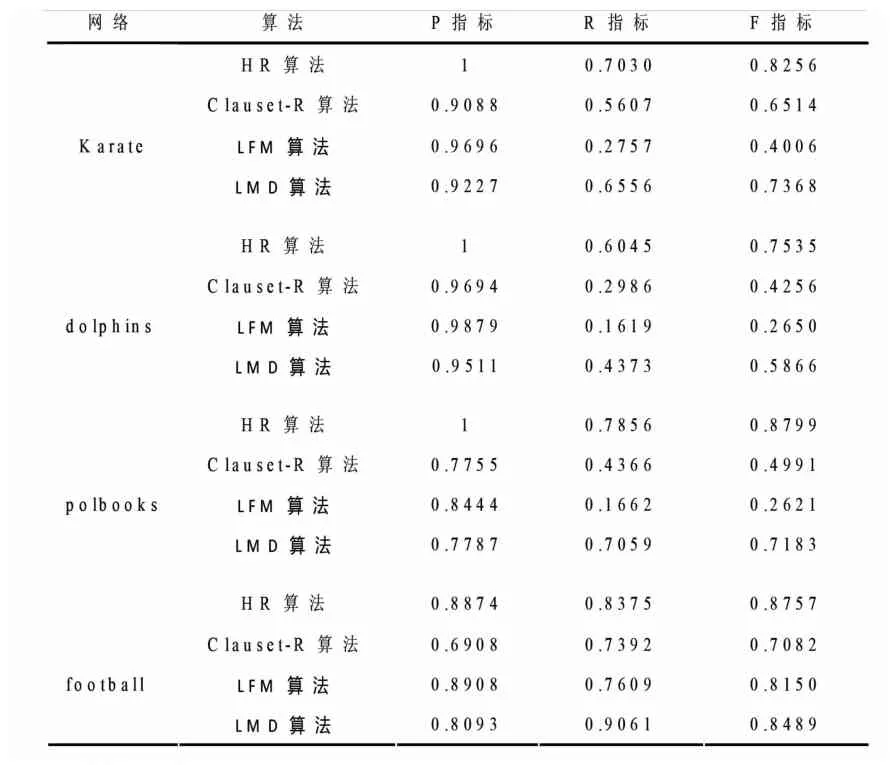
表2 HR算法与其它算法在四个网络实验中的结果

综合评价指标在F在P指标和R指标双重影响下，大致会呈现先增加后减小的趋势。于是，这里就会有参数α当取得什么值的时候F最大的问题存在。不同的网络，最优参数α的取值显然不同。最终是希望能找到这个最优参数α，如在Karate网络中当a=0.45时F=0.974要远远优于大致取的α= 0.6的情况；在polbooks网络这种情况更甚，当α= 0.3时F=1，也就是说无论从哪个节点开始扩张找到的社团都与实际相符。因此寻找最优α或寻找是什么因素在影响最优参数α的取值对提高算法的精确度有很大的帮助。

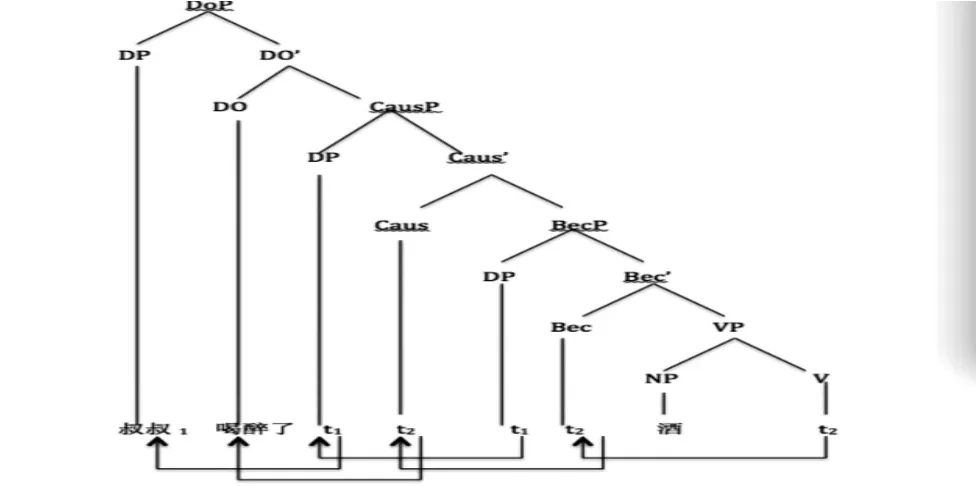
图3 HR算法评价指标随着参数变化图

首先定义网络平均相对相似度为Mean-RS网络中所有不为零的相对相似度（计算如公式3）的平均值。如图4所示发现参数α的最优值与网络平均相对相似度成正相关。这很容易理解，参数α就是通过网络相对相似度来控制节点的朋友集合，网络的平均相对相似度越大，参数α的设置应该相应的增大。

结束语

本文基于关系的层次性设计了一种局部社团探测方法。该算法根据一个参数α和节点的相对相似度定义该节点的朋友与最好朋友集合。然后提出三条假设：（1）节点和它的最好朋友同属于一个社团；（2）两个节点互为朋友在一个社团；（3）节点的大多数朋友在一个社团，则这个节点也属于这个社团。基于此，通过设计的算法可以给出任意节点所在的社团。实验表明效果优于当前的同类算法。最后，本文还讨论了最优参数α的取值问题，虽然发现了参数α的最优值与网络的平均相对相似度成正相关，这只能指导对参数的取值，但是最后还是无法精确给出在什么时候可已得到最好的扩张结果，这将是以后研究的内容。

Local community detection based on the hierarchy in relations

ZOU Bin

Community structure detection bears both theoretical and practical significance for the study of complex systems.The local community detection is one of its main challenges.Now,there is little research based on local community detection methods,and the precision of most of algorithm is low.Hence we consider the hierarchy in relations,through the relative similarity of the nodes and the concept of friend and best friend defined by a parameter.Three hypotheses are presented.Through the three hypotheses,we design the local community detection algorithm based on the hierarchy in relations(HR).The experimental results show that our algorithm is superior to the similar algorithm.Finally,we found that the optimal value of parameters is proportional to the network of average relative similarity through analysis.

community structure;local community detection;hierarchy in relations;friend;best friend

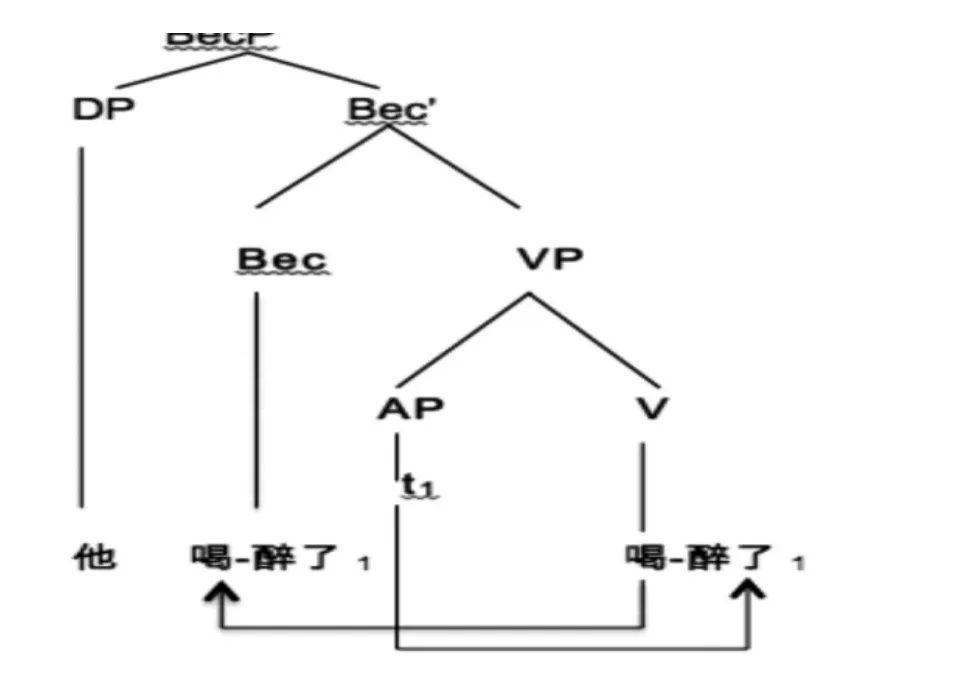
图4 最优参数和网络平均相对相似度的关系图

TP399

A

1009-9530（2016）05-00111-05

2015-12-30

安徽省高校优秀青年人才支持计划重点项目“基于动态时序模糊软集的不确定性信息度量模型研究与应用”（gxyqZD2016453）；安徽广播电视大学青年基金项目“基于时序模糊软集金融风险预警数学模型”（qn15-20）

邹斌（1981-），男，安徽广播电视大学讲师，硕士，研究方向：智能计算和复杂网络。