光子晶体光纤中正啁啾对色散波及孤子俘获的调控作用
黄 颖
(湖南大学 信息科学与工程学院,微纳光电器件及应用教育部重点实验室,湖南 长沙 410082)
光子晶体光纤中正啁啾对色散波及孤子俘获的调控作用
黄 颖*
(湖南大学 信息科学与工程学院,微纳光电器件及应用教育部重点实验室,湖南 长沙 410082)
基于飞秒脉冲在光子晶体光纤中传输时所遵循的非线性薛定谔方程, 利用数值模拟的方法研究了脉冲初始正啁啾在超连续谱的产生过程中对色散波及孤子俘获的影响.结果表明:正啁啾能显著提升色散波的产生效率,且色散波的强度与啁啾值成正比.当啁啾值不超过某一临界值且满足相位匹配条件时,孤子和色散波之间的四波混频效应能产生俘获波,俘获波的强度与孤子能量及色散波强度有关.因此,选择合适的啁啾值,利用正啁啾对色散波及俘获波的调控作用可以提高超连续谱蓝端的能量分部.
超连续谱;啁啾;色散波;孤子俘获
自2000年超连续谱首次在光子晶体光纤(PCF)中被观测到以来[1],PCF以其可控的色散特性、无止尽单模特性及高非线性特性,与传统光纤相比具有独特的优势,PCF以及超连续谱的很多潜在应用为非线性光纤光学领域的研究注入了新的活力[2-3].当飞秒脉冲在光纤的反常色散区泵浦,理想条件下通常是以高阶孤子的形式传输的.受拉曼扰动和高阶色散影响[2-4],高阶孤子分裂成基阶孤子,同时,在满足相位匹配的光纤的正常色散区,会伴随着色散波的产生,能量不断向色散波转移.特别是在双零色散光纤中,由于其不仅拥有正的色散斜率,而且具有负的色散斜率,可同时观察到蓝移色散波(B-DW)和红移色散波(R-DW)[5].色散波能极大地展宽频谱,是超连续谱形成的重要物理机制.进一步地,孤子在拉曼效应的影响下不断红移,当孤子和色散波的走离长度足够短时,孤子和色散波会发生四波混频过程,产生新的频率成分,该频率成分叫做俘获波[5-8].
关于色散波的产生,Dudley和Genty等人于2006年发表的文献上对其进行了详细的介绍[2].近年来,孤子俘获现象成为人们的研究热点.最早对于光纤中孤子俘获的理论预测是由Curtis R. Menyuk 完成的[9],Nishizawa于2002年最早在实验中发现孤子俘获现象(正常色散区的波包频谱蓝移).2005年, Skryabin和Yulin认为孤子和色散波之间的四波混频(FWM)是蓝移俘获波包产生的真正原因[6].2013年,Wang 等人发现孤子不仅可以俘获蓝端的色散波,而且可以俘获红端的色散波[5].随后Zhao 等人研究了三个零色散光纤中的孤子俘获现象[10].[11][12]研究了色散斜率对孤子俘获的影响,指出自陡峭效应抑制红端的色散波产生及孤子俘获,而蓝端则得到加强.近来,Yang 等人研究了啁啾对色散波产生及孤子俘获的影响,发现正的啁啾有利于色散波的产生,而负的初始啁啾抵消掉自相位调制产生的频率啁啾,从而抑制蓝端色散波的产生[13].本文就初始正啁啾对色散波及孤子俘获效应的影响进行了更具体的研究,正啁啾在一定范围内调谐,可使色散波的产生效率最大化;同时探究在这一过程中对孤子俘获的影响,选取合适的啁啾值来获得理想的超连续谱光源.
1 数值模型
飞秒脉冲在PCF中的传输模型采用广义非线性薛定谔方程,其表达式如下:

(1)
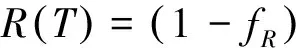
在孤子分裂过程中,孤子不断向色散波转移能量,而色散波的中心波长由下面相位匹配条件来决定:

(2)
β(ωp)和β(ωDW)分别表示色散波和泵浦波中心频率处的传输常数,Pp表示泵浦功率.从上式可推知,当β3>0时,会在短波长处辐射出蓝移色散波,而β3<0时,会在长波长处辐射出红移色散波.因此在双零色散光纤中可同时观察到两种色散波.此外,当色散波和孤子满足群速度匹配条件时[5],会发生孤子俘获现象,产生新的频率成分,这对于获得超平坦的超连续谱有重要意义.
2 数值结果与讨论
本文所有的模拟均采用双零色散光纤,光纤的群速度曲线和群时延曲线如图1所示.两个零色散点分别位于655 nm和930 nm,区间[655 nm,930 nm]为反常色散区,而两侧是正常色散区.泵浦波长位于反常色散区的725 nm,泵浦峰值功率维持在200 W,孤子阶数N=5.由于模拟中光纤长度均为60 cm,所以光纤损耗忽略.啁啾参量C取值为正.
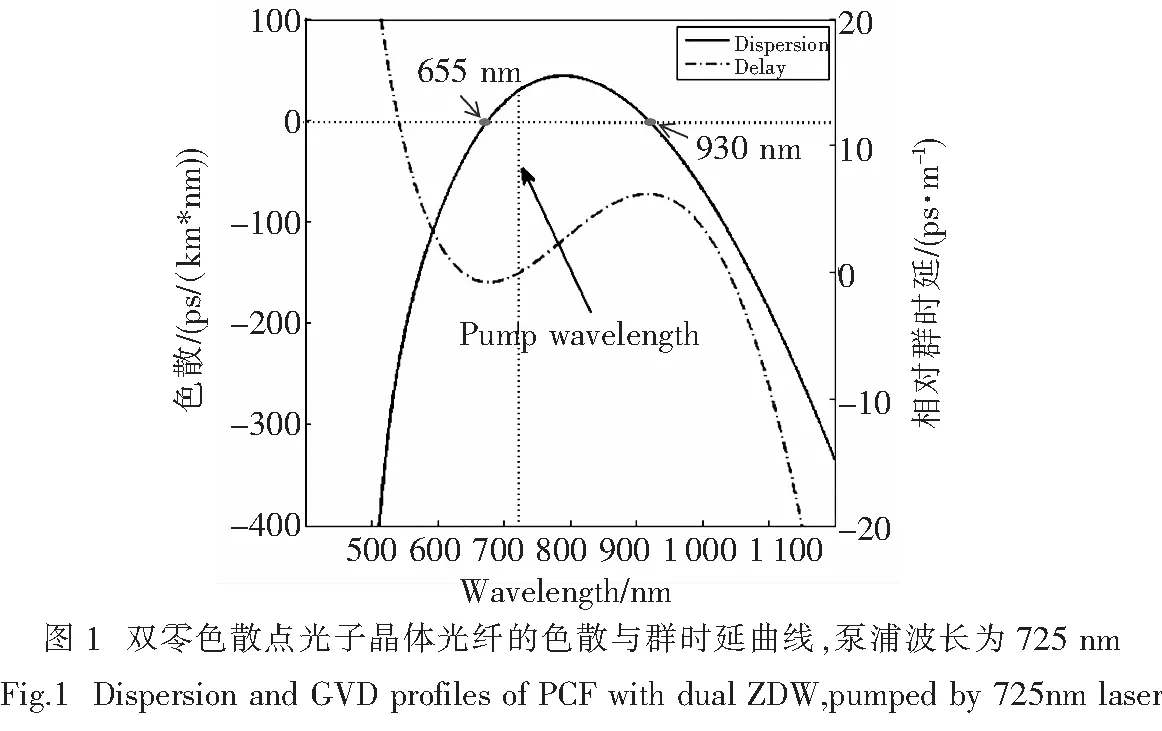
基于广义非线性薛定谔方程,讨论双零色散点光子晶体光纤中正啁啾对色散波产生及孤子俘获的影响.图2为输入脉冲随传输距离的时域演化图,(a)图初始啁啾为零,(b)图中C=3.输入脉冲在经历时域压缩之后开始孤子分裂,可以明显地看到几个孤子分裂出来,并伴有大量的色散波产生,拉曼孤子在拉曼诱导的孤子自频移(RIFS)下开始红移,形成超连续谱.第一个分裂出来的孤子能量最大,也获得最大的频移.对比(a)图和(b)图,可以发现几点:(1) 在有啁啾的情况下,色散波产生所需的光纤长度更短;(2) (b)图中的孤子能量低;(3) 啁啾导致色散波产生的效率更高.主要的原因是啁啾所产生的频率和自相位调制(SPM)所产生的频率啁啾同号,因此加速脉冲的时域压缩,当达到极限时发生孤子分裂.因此在啁啾条件下色散波的能量和产生效率上都得到加强.
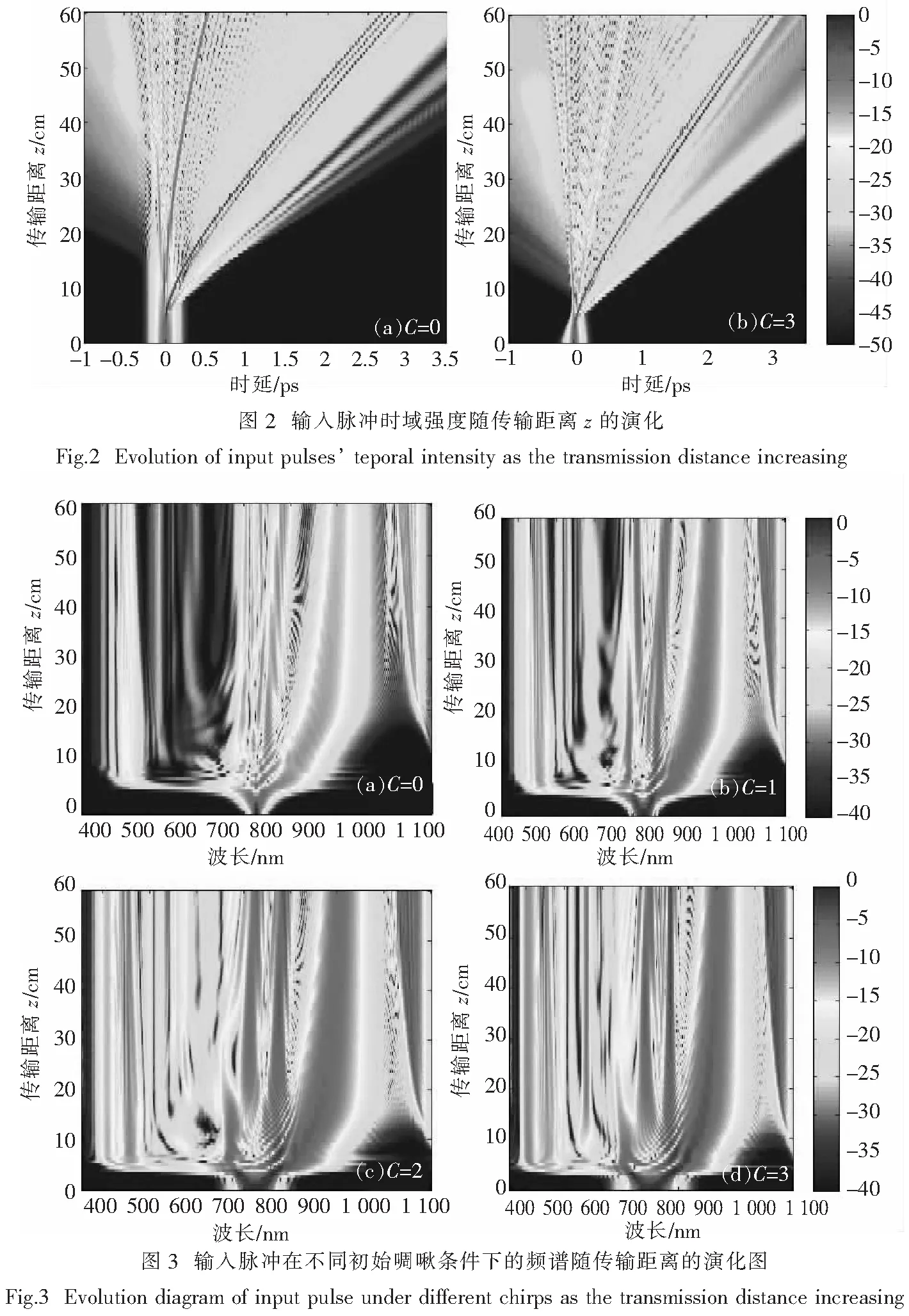
为了更详尽地讨论啁啾对色散波和孤子俘获产生的影响.图3为N=5时, 输入脉冲沿光纤长度频域的演化图.如图3所示,在z=5 cm之前频谱的演化主要表现为由自相位调制导致的对称的频谱展宽.随后,高阶色散和拉曼散射的影响导致孤子的分裂, 形成一个基阶拉曼孤子.随着脉冲不断传输,在两个正常色散区辐射出蓝移色散波(B-DW)和红移色散波(R-DW),在孤子红移的过程中,色散波不断被放大.由于频谱反冲效应的存在,孤子不会一直红移,最终停留在第二个零色散点附近[3].在图3中,随着啁啾不断增大,可以发现无论是B-DW还是R-DW的强度都在不断增大,使得整个频谱范围内都存在频谱分量.而且有啁啾时,色散波也产生得更早,对比(a)图和(d)图,(a)图中B-DW产生于大约5 cm处,R-DW约在12 cm处产生并放大;(b)图中B-DW仅传输3 cm就已产生,R-DW也在7 cm处产生.总之B-DW的产生效率简单地随正啁啾的增大而线性增大,这对于调节B-DW所占输入脉冲总能量是很方便的,当然啁啾参量不能无限增大,不能超过其临界值,因为C过大,根本就不能形成孤子,也就不会发生孤子俘获[4].
从频谱的演化图并不能很好地研究啁啾对孤子俘获效应的影响,因此,图4为啁啾分别为1、2、3时的时频图,图的对比度均在-40 dB.
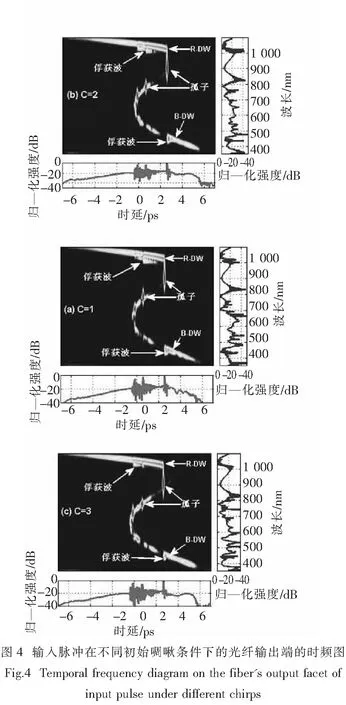
从图4可以看到,由于在双零色散光子晶体光纤第一个零色散波长附近色散斜率为正,而在第二个零色散波长附近色散斜率为负,因此,由相位匹配条件可知,孤子在第一个零色散波长附近(约600 nm处)辐射出B-DW, 而当孤子红移至第二个零色散波长附近(约950 nm处)时则辐射出R-DW.高阶孤子分裂出数个基阶孤子,并且最先分离出来的孤子相比第二个孤子具有更大的强度, 更宽的频谱宽度, 更大的拉曼感应频移.除此之外,我们还发现了一些新的频谱峰,即俘获波,这主要是由群速度匹配条件满足时,孤子和色散波之间的四波混频(FWM)效应产生的.图4中的时频图呈现出的“Z”字形与图1中的群时延曲线是一致的.由图4(a)~(c),随着啁啾逐渐增大,蓝端色散波出现长长的拖尾,这对于频谱向深蓝处发展很有意义;蓝端俘获波的强度也在增强,尽管没有像色散波那样明显,这主要是由于色散波大的时延导致的孤子与色散波之间走离长度过大引起的,也就是说虽然俘获波强度与色散波强度有关,但大的群速度失配同样导致俘获效应的削弱.而在红端,R-DW强度的增强没有蓝端明显,俘获波的强度在一定的啁啾范围内还是增强的.总之,当啁啾取合适值时,B-DW和R-DW能量的增强、蓝端色散波长长的拖尾及俘获波能使超连续谱更平坦,能量分布更均匀,也有利于对超连续谱产生过程的理解.
3 结 论
基于广义的非线性薛定谔方程, 采用分步傅立叶算法数值模拟了飞秒脉冲在双零色散点光子晶体光纤中的传输,探究了正啁啾对色散波的产生及孤子俘获效应的影响.数值结果表明: 正啁啾在一定范围内线性增大时,色散波的强度以及色散波的产生效率也线性增强,特别是,啁啾值增大到一定程度时,在短波长处会产生长长的拖尾,这有利于超连续向深蓝发展;蓝端的孤子俘获效应也在一定程度上得到加强,不过由于色散波和孤子之间的群速度失配,增强并不太明显;红移色散波也能在相对短的传输距离处产生,能量随之增大.综合这些效应,选取合适的啁啾值可获得理想的超连续谱光源.
(作者兼任湖南交通职业技术学院讲师)
[1] RANKA J K,WINDELER R S,STENTZ A J.Visible continuum generation in air-silica microstructure optical fibers with anomalous dispersion at 800 nm[J]. Opt Lett,2000,25: 25-27.
[2] DUDLEY J M,GENTY G,COEN S.Supercontinuum generation in photonic crystal fiber[J]. Rev Mod Phys,2006,78(4):1135-1184.
[3] ROY S,GHOSH D,BHADRA S K,et al.Role of dispersion profile in controlling emission of dispersive waves by solitons in supercontinuum generation[J]. Opt Commun, 2010, 283:3081-3088.
[4] LATAS S C V,FERREIRA M F S.Soliton propagation in the presence of intrapulse Raman scattering and nonlinear gain[J]. Opt Commun, 2005, 251:415-422.
[5] WANG W,YANG H,TANG P,et al.Soliton trapping of dispersive waves in photonic crystal fiber with two zero dispersive wavelengths[J]. Opt Express,2013, 21:11215-11226.
[6] SKRYABIN D V,YULIN A V.Theory of generation of new frequencies by mixing of solitons and dispersive waves in optical fibers[J]. Phys Rev E Stat Nonlin Soft Matter Phys,2005,72(1):016619.
[7] GORBACH A V,SKRYABIN D V,STONE J M,et al.Four-wave mixing of solitons with radiation and quasi-nondispersive wave packets at the short-wavelength edge of a supercontinuum[J]. Opt Express,2006,14(21):9854-9863.
[8] HILL S,KUKLEWICZ C E,LEONHARDT U,et al.Evolution of light trapped by a soliton in a microstructured fiber[J]. Opt Express,2009,17(16):13588-13600.
[9] MENYUK C R.Stability of solitons in birefringent optical fibers. I: Equal propagation amplitudes[J]. Opt Lett, 1987, 12: 614-616.
[10] ZHAO S,YANG H,CHEN N,et al.Soliton trapping of dispersive waves in photonic crystal fiber with three zero-dispersive wavelengths[J]. IEEE Photonics Journal,2015,7:7102709.
[11] ROY S,BHADRA S K,AGRAWAL G P.Effects of higher-order dispersion on resonant dispersive waves emitted by solitons[J]. Opt Lett, 2009,34:2072-2074.
[12] YANG H,HAN F,HU H,et al.Spectral-temporal analysis of dispersive wave generation in photonic crystal fibers of different dispersion slope[J]. Journal of Modern Optics, 2014,61:409-414.
[13] YANG H,ZENG Q,HU H,et al.Impact of chirp on soliton trapping of dispersive waves in photonic crystal fiber with two zero dispersive wavelengths[J]. Opt Commun, 2014, 325:170-174.
责任编辑:龙顺潮
The Regulation and Control of Positive Chirp over Dispersive Wave and Soliton Trapping in PCF
HUANGYing*
(Key Laboratory for Micro/Nano Optoelectronic Devices of Ministry of Education, College of Computer Science and Electronic Engineering,Hunan University, Changsha 410082 China)
This paper discusses the effects that positive chirps have on the dispersive waves and soltiton trapping based on nonlinear Schödinger equation during the femtosecond pulses transmitted in the PCF by using the method of numerical simulation.The result shows: positive chirps can promote the efficience of dispersive wave generation dramatically, and the intensity of dispersive wave is proportional to the values of chirps. When the values of chirps don’t exceed some critical value and meet the phase matching, the trapping waves, whose intensity has something with soliton energy and dispersive intensity, is generated by the FWM between solitons and dispersive waves. So we can improve the blue-shift energy of SC spectrum by using positive chirp which can regulate and control dispersive waves and trapping waves.
supercontinuum spectrum;chirp;dispersive wave;soliton trapping
2016-04-07
国家自然科学基金项目(61275137);教育部新世纪优秀人才支持计划( NCET-12-0166)
黄 颖(1973—),湖南 汩罗人,博士研究生,高级工程师.E-mail:david_hy@hnu.edu.cn
O436.2
A
1000-5900(2016)04-0010-05

