基于改进PSO-NN的径流水位预报研究
蒋林利
(1.广西科技师范学院 数学与计算机科学学院,广西 来宾 546199;2.武汉大学 软件工程国家重点实验室,湖北 武汉 430070)
基于改进PSO-NN的径流水位预报研究
蒋林利1,2*
(1.广西科技师范学院 数学与计算机科学学院,广西 来宾 546199;2.武汉大学 软件工程国家重点实验室,湖北 武汉 430070)
为了提高河流日径流水位预报的精确度,针对粒子群算法和神经网络存在的缺陷,提出一种新的粒子群算法进化三层前馈神经网络的连接权系和阈值,并以此建立逐日径流水位预报模型.该算法采用跟随变异粒子扰动变化的惯性权重和学习因子来提高粒子群算法的局部、全局搜索性能和收敛速度.实验仿真结果表明,在收敛速度和预测的精确度上,该模型明显优于其他对比模型,为获得更高预测精度的径流水位预报提供了一种有效的建模方法.
神经网络;粒子群;日径流水位预报;惯性权重;学习因子
高效的径流预报对水资源调度和管理具有非常重要的意义,传统的预报方法如时间序列法、多元线性回归法等很难考虑到预报变量和预报因子之间的非线性关系,因此,径流预报的精度不高.近年来,人工神经网络(Neural Networks, NN)方法被成功地应用在大气学科和径流预测建模等各个复杂领域[1-3].虽能处理径流预报因子之间复杂的非线性问题,但神经网络训练过程中还没有确定各个参数的定量方法,存在不稳定性和过拟合学习、收敛速度慢等缺陷[3-4].为了解决上述问题,研究者们利用智能算法来优化神经网络[5-7].其中,具有强大寻优能力的粒子群优化(Particle Swarm Optimization, PSO)算法优化神经网络已成为研究的热点[8-13].目前,国内外研究者提出了许多改进的PSO算法,如反向学习策略PSO算法[14-15]、非线性递减惯性权重PSO算法、自适应变化PSO算法和随机权重PSO算法等,这些改进的PSO算法在处理高维复杂问题寻优过程中仍存在陷入局部最优、收敛速度慢等缺点[16-17].[18]采用跟随变异粒子扰动变化策略来改进惯性权重的PSO算法,有效地避开了陷入局部最优问题,提高了收敛速度和寻优精度.
为了进一步改善算法性能、提高径流预报的精度,在[18]的基础上,采用一种同时改进惯性权重和两个学习因子的粒子群算法来优化前馈神经网络,从而加强粒子的搜索能力,使算法能够跳出局部极值和具有更好的泛化性能,并以此建立预测模型.以广西柳州历年日径流水位进行实例分析,与标准粒子群优化的前馈神经网络预测模型、随机惯性权重粒子群优化神经网络预测模型比较,结果说明,提出的改进PSO前馈神经网络模型具有更高的预测精度和较好的稳定性.
1 相关技术
1.1 神经网络(NN)
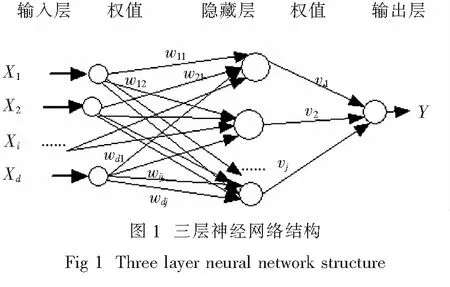
图1所示为三层前馈神经网络模型,每个神经元操作均为加权输入总和,通过一个非线性激活函数(Sigmoid函数)来传递.神经元的输出值表示为:
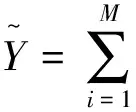
其中Xi是输入因子矩阵,n为粒子的维数,wij为输入层与隐藏层间的连接权值,wjk为隐藏层与输出层之间的连接权值,wj0为第j个神经元的阈值,wk0为第k个神经元的阈值.网络的激活函数为Sigmoid函数:f(x)=1/(1+exp(-x)).
1.2 标准PSO算法
PSO算法使用数学表示为:
uij(t+1)=w·uij(t)+c1r1(pi(t)-xij(t))+c2r2(pg(t)-xij(t)) ,
(1)
xij(t+1)=xij(t)+uij(t+1) ,
(2)
其中uij(t) 为当前粒子速度向量,uij(t+1)和xij(t+1)分别表示第i个粒子通过第t次迭代后的速度和位置,w是惯性因子(一般取值为[0,-1]),控制局部和全局搜索平衡的能力,pi(t)表示当前个体“极值”,pg(t)表示当前群体的全局“极值”, c1和c2为学习因子(通常取值均为2),选择合适的c1和c2值既可加快收敛速度又不容易陷入局部最优.γ1和γ2都是在[0,1]之间的随机数.
2 提出的改进PSO算法
选取合适的惯性权重对PSO算法的性能和效率起着非常重要的作用.为了充分利用惯性权值和学习因子的特点,采用跟随变异粒子扰动变化来调整惯性权重大小以提高PSO算法的性能.其主要思想是根据粒子散布位置的均方差来判断粒子是否趋于一致,在寻优过程中,当判断粒子趋于一致时,就对该粒子执行扰动操作,使该粒子发生变异,使得粒子在搜索过程中保持多样性特点,这样避免出现粒子陷入局部最优的现象;同时也依据该粒子变异程度对惯性权重做出相应的调整.改进后的PSO算法能更好地保持粒子种群的多样性和有效地提高全局搜索能力.
利用粒子散布位置相似度来判定粒子xi是否趋于一致性,如(3)式:

(3)
其中d是表示粒子散布位置的均方差值;当d值小于给定的阈值(0.1)时,该粒子趋于一致;m表示粒子的数量.当粒子出现一致性时,对该粒子状态施加扰动,其扰动操作表示为:
xitem=xiold+σ ,
(4)
其中xitem是执行变异操作后的粒子状态;σ是随机扰动量,确保变异后的粒子状态仍然处在搜索空间内.惯性权重的大小根据变异粒子扰动程度大小进行动态调整,其公式如下:
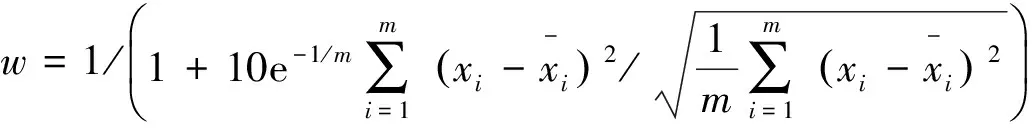
(5)
异步学习因子表示如下:
c1=c1ini-(c1ini-c1fin)(k/Tmax), c2=c2ini-(c2fin-c2ini)(k/Tmax),
(6)
其中初始化c1ini和c2ini分别设为2和0.5,迭代终值c1fin和c2fin分别为0.5和2,k是当前的迭代次数,Tmax为最大迭代次数.粒子群在优化过程中的适应度函数定义如下:
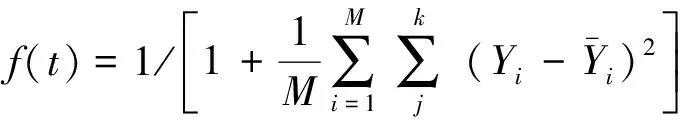
(7)
其中Yi是实际输出值.
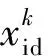
3 径流实例建模分析
本文采用的数据来自中国西南部的广西柳江流域,它是西江流域排水最主要的支流之一.其干流全长773.3 km,年均流量为1 866 m3/s,本建模研究的对象是柳州站平均日流量数据及观察到的径流水位.该径流水位预测的数据集包含2007年到2010年的1 460个数据点,其中1 095个训练样本集,365个测试样本.
3.1 参数设置
改进PSONN在WIN7系统上运行,软件编程环境为Matlab7.0.实验中,种群数设为40,最大迭代次数为100,粒子初始化的位置和速度上下界均为-1和1,改进的算法中设置的初始惯性权重值为0.7,随着迭代次数的增加,在寻优过程中粒子变异扰动使惯性权重值在[0,1]之间变化,最优网络结构为8-8-1(分别表示各层的神经元个数).进行对比的标准PSO的惯性权重的范围为[0.1,0.9],学习因子c1=c2=2.

表1 3种预报模型对2010年径流水位预报的性能分析
3.2 结果分析
在改进PSONN 进化训练过程中,训练样本的适应度值随进化次数的增加,逐渐趋于平稳.适应度值在训练样本过程中有多处停滞的现象出现,这些现象说明改进的PSONN在寻优中陷入了局部解.由于采用紧随粒子变异扰动来调整惯性权重值,能快速跳出局部最优,搜索到后期也不容易发生停滞的现象,有利于快速收敛到全局最优解.
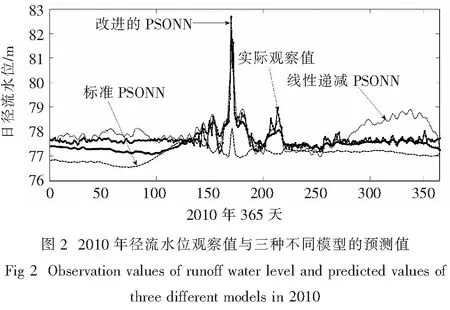
从图2可以看出,提出的PSONN预测模型具有更高的精确度并更能准确地捕获跟踪水位变化过程.从表1给出的3个参考指标可以看出,PSONN模型性能最好,其平均相对误差和均方根误差均是最小的,说明其具有更高的预测精度.
4 结 论
针对粒子群算法存在的缺点以及复杂环境的径流预报难的问题,本文对粒子群算法的惯性权重进行改进,并以此建立广西柳江径流水位预测模型.该模型利用PSO算法中变异粒子扰动变化的程度来动态地调整惯性权重值,避免了陷入局部最优解,使其更快速收敛到全局最优解,提高了神经网络的性能.与常用的标准的和随机的粒子群预报对比,更能准确地刻画径流水位变化的趋势,预测的精确度更高,为径流预报提供了一种参考模型.
[1] 蒋林利, 吴建生, 曾文华. 基于混合算法的径流预报模型研究[J]. 广西大学学报(自然科学版), 2014, 39(2): 351-357.
[2] 董晓华, 刘超, 喻丹,等. 基于平均线性粒子群算法的人工神经网络在径流预报中的应用[J]. 水文, 2013, 33(5): 10-15.
[3] 吴建生,刘丽萍, 金龙.粒子群-神经网络集成学习算法气象预报建模研究[J]. 热带气象学报, 2008, 24(6): 679-686.
[4] TAHER N,EHSAN A, MASOUD J.A new hybrid evolutionary algorithm based on new fuzzy adaptive PSO and NM algorithms for distribution feeder reconfiguration [J]. Energy Conversion and Management, 2012, 54(3): 7-16
[5] WU J S. An effective hybrid semi-parametric regression strategy for rainfall forecasting combining linear and nonlinear regression[J]. International Journal of Applied Evolutionary Computation,2011, 2(4): 50-65.
[6] LI Y J,LI Y,LI F,et al. The research of temperature compensation for thermopile sensor based on improved PSO-BP algorithm[J]. Mathematical Problems in Engineering,2015(3):1-6.
[7] 蒋林利, 李洁. 基于改进粒子群算法的神经网络在月降水预报中应用[J]. 柳州师专学报, 2014, 29(1): 126-130.
[8] 卢辉斌, 李丹丹, 孙海艳. PSO优化BP神经网络的混沌时间序列预测[J]. 计算机工程与应用, 2015, 51(2): 224-229.
[9] 高峰, 冯民权, 滕素芬. 基于PSO优化BP神经网络的水质预测研究[J]. 安全与环境学报, 2015, 15(4): 338-341.
[10] NEYESTANI M, FARSANGI M M, NEZAMABADI-POUR H. A modified particle swarm optimization for economic dispatch with non-smooth cost functions[J]. Engineering Applications of Artificial Intelligence, 2010, 23(7):1121-1126.
[11] 王新, 孙河南. 基于粒子群神经网络的级联式变频器故障诊断[J]. 计算机仿真, 2015, 32(7): 421-425.
[12] 杨建辉, 吴聪. PSO 结合 SA 优化算法的无线传感器网络路由协议[J]. 湘潭大学自然科学学报, 2015, 37(4): 98-104.
[13] 蒋林利. 改进的PSO算法优化神经网络模型及其应用研究[D]. 厦门:厦门大学, 2014.
[14] 夏学文, 刘经南, 高柯夫,等. 具备反向学习和局部学习能力的粒子群算法[J]. 计算机学报, 2015, 38(7): 1397-1407.
[15] 汪慎文,丁立新,谢大同,等. 应用反向学习策略的群搜索优化算法[J].计算机科学,2012,39(09): 183-187.
[16] JORDEHI A R, JASNI J. Parameter selection in particle swarm optimization : a survey[J]. Journal of Experimental & Theoretical Artificial Intelligence, 2013, 25(4):527-542.
[17] 周燕, 刘培玉, 赵静,等. 基于自适应惯性权重的混沌粒子群算法[J]. 山东大学学报, 2012, 47(1): 27-32.
[18] 邢焕革, 卫一熳. 跟随变异粒子扰动变化的惯性权重PSO算法[J]. 四川兵工学报, 2015, 36(1): 106-110.
责任编辑:龙顺潮
Research on Runoff Water Level Prediction Based on Improved PSO-NN
JIANGLin-li1,2*
(1.School of Mathematics and Computer Science, Guangxi Science & Technology Normal University, Laibin 546199; 2. State Key Lab of Software Engineering, Wuhan University, Wuhan 430070 China)
In order to improve forecasting accuracy of the rivers diameter water level, the paper puts forward a new particle swarm optimization algorithm evolving connection weights and threshold of three layer feedforward neural network,and establishes forecasting model of the daily runoff water level. In this algorithm, the mutation particles disturbance change inertia weight adjustment strategy and learning factor is used to improve the local and global search performance and convergence rate of the particle swarm optimization algorithm. The simulation experimental results show that the convergence speed and prediction accuracy of the model is better than other comparative model.It provides an effective modeling method in order to obtain higher prediction precision of runoff water level forecast.
neural network; particle swarm optimization; daily runoff prediction; inertia weight; learning factor
2016-02-21
广西省自然科学基金项目(2014GXNSFAA118027);广西高校科学技术研究项目(LX2014498,YB2014467);2014年来宾市科学研究与技术开发计划项目
蒋林利(1976—),女,广西 桂林人,副教授.E-mail:jll200@163.com
TP183
A
1000-5900(2016)04-0067-04

