错在哪里
2016-02-07 06:46:28黑龙江省鸡西市一中
中学数学教学 2016年6期
1 黑龙江省鸡西市一中
王荣峰 (邮编:158100)
数学园地
错在哪里
1 黑龙江省鸡西市一中
王荣峰 (邮编:158100)
该题为广西南宁市第四十二中学潘普昂老师发表在《中学数学》2016年第7期的论文《求函数值域方法探析》中的例5.
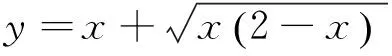
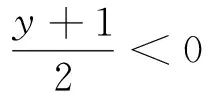
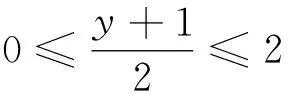
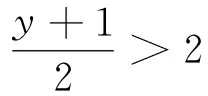
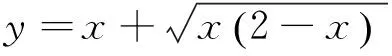
解答错了!错在哪里?
正确解法1 直接求根
评注 直接求根,注意到平方的不等价并进行补救,便可求出该函数的值域,这也是处理此类无理函数值域的一种十分有效的方法.
正确解法2 用不等式
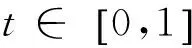

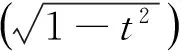
正确解法3 三角换元
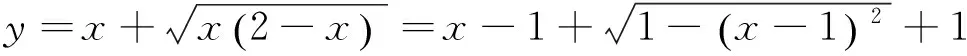
评注 通过三角换元将问题转化为求三角函数的值域,这是处理此类无理函数值域问题最简洁的办法,解题的关键在于合理确定角θ的范围.
正确解法4 借助求导
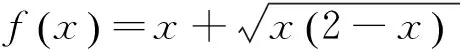
评注 自导数引入高中数学教材后,为解决函数最值(值域)问题提供了强有力的工具,已经成为解此类题的一般性方法.
教学实践证明,坚持对典型的易错题进行深刻的剖析,不但可以加深对知识的理解,提高解题的准确率,同时还有利于形成缜密的思维品质.
2 江苏省海州高级中学
冯善状 (邮编:222023)
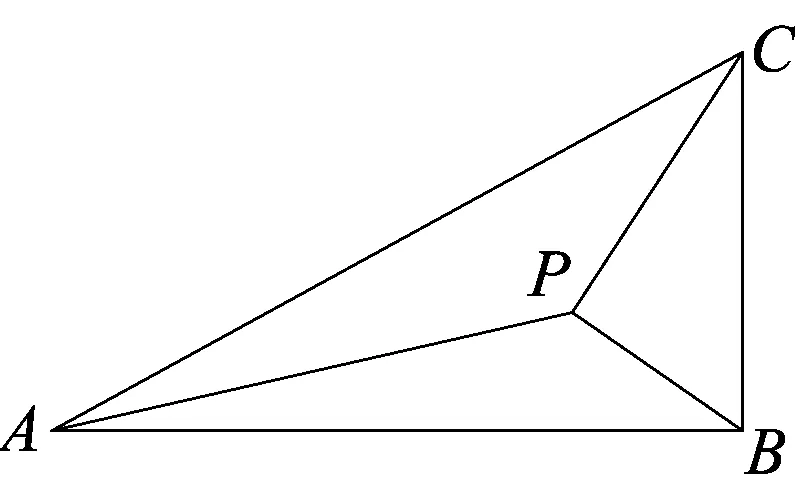
错解
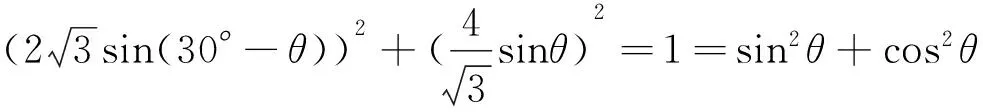
解答错了!错在哪里?
解答过程弱化了题中隐含条件,△BPC中除了通过勾股定理刻画∠BPC为直角,还应体现∠BCP=θ.事实上,上述做法在刻画△BPC边角关系时,有顾此失彼之嫌!
考情说明 该题是江苏省海州高级中学高三8月份考前检测试题,上述解答过程由学生考卷所提供。考后点评时,95%学生不能对上述错误的解答过程作出纠正。
猜你喜欢
——鸡西市城子河区树英小学简介
黑龙江教育(教育与教学)(2024年2期)2024-03-07 00:40:58
江苏地方志(2023年6期)2024-01-18 07:07:48
江苏农村经济(2023年9期)2023-09-28 08:40:38
连云港师范高等专科学校学报(2021年4期)2021-03-04 05:45:24
连云港师范高等专科学校学报(2021年4期)2021-03-04 05:45:22
黑龙江水利科技(2020年8期)2021-01-21 09:27:36
中学数学杂志(初中版)(2020年6期)2020-01-06 03:35:20
江苏科技报·E教中国(2019年8期)2019-09-10 07:22:44
新教育时代·教师版(2018年17期)2018-07-21 09:39:38
祖国(2017年21期)2018-01-02 00:55:21

