基于BCS-SPL压缩感知算法的纸病图像重构
周 强 胡江涛 王志强 张俊涛
(陕西科技大学电气与信息工程学院,陕西西安,710021)
·纸病图像重构·

基于BCS-SPL压缩感知算法的纸病图像重构
周 强 胡江涛*王志强 张俊涛
(陕西科技大学电气与信息工程学院,陕西西安,710021)
随着造纸工业纸机速度和纸幅宽度的增长,传统的纸病检测处理方式面临着图像数据传输量剧增,纸病检测系统难以实现实时性处理的问题。压缩感知理论能够有效降低数据的采样量,但将压缩感知应用于二维纸病图像时,面临着重构纸病图像质量不高的问题。本研究采用分块压缩感知(BCS)-平滑投影Landweber(SPL)重构算法对纸病图像进行重构,并着重研究了该算法在不同采样率和不同图像分块大小下的重构效果。实验结果表明,在压缩感知框架下,通过BCS-SPL算法重构的低采样率纸病图像具有较高的图像质量,有效降低了纸病图像数据的传输量。
压缩感知;BCS-SPL重构算法;纸病图像重构
在造纸生产过程中,由于造纸原料存在问题、纸机设备老化、生产过程存在误操作等原因,生产出的纸张可能会存在孔洞、污点、裂缝等缺陷。为了保证生产纸张的质量,需要在造纸过程中对纸张表面进行纸病实时检测。目前一般采用机器视觉技术实现对纸张的检测,即通过图像采集装置获取图像,将图像传送至处理单元,利用数字图像处理技术进行目标识别和检测,进而根据检测结果调整现场设备[1-2]。随着造纸工业的发展,纸机的速度越来越快,纸幅越来越宽,相机采集到的数据大幅增加,从而消耗大量CPU资源,大大减缓系统的处理速度,给纸病检测系统的实时性造成压力,因此纸病检测系统数据传输量大的问题亟待解决。
压缩感知(Compressed Sensing,CS)理论是一种新的指导信号采集传输的理论,能够在采样的同时实现数据的压缩处理[3- 4],避免传统采样模式下采集大量数据所带来的资源消耗,有效减少数据的传输量。然而,将压缩感知应用到二维图像中,主要面临随机测量矩阵所需存储量大和重构图像质量不高的问题。分块压缩感知(Block Compressed Sensing,BCS)将图像分成大小相等的块图像,并对每块图像单独处理,减小了测量矩阵的大小,使得测量矩阵便于存储和传输,数据传输的实时性得到显著提高[5- 6]。对于图像的重构质量,本研究采用一种基于分块图像重构的平滑投影Landweber算法(Smoothed Projected Landweber,SPL),SPL算法以图像平滑和稀疏作为先验条件,有效地改善了重构算法的复杂性,得到了广泛应用。
本研究首先对纸病图像进行压缩采样处理,然后对BCS-SPL重构算法进行研究,并对经过压缩采样的纸病图像进行重构处理,将重构纸病图像的峰值信噪比(PSNR)和结构相似性指标(SSIM)作为评价重构图像的客观和主观标准,以重构时间作为算法复杂度的度量,研究纸病图像在不同块大小和不同采样率下的重构效果。
1 CS理论框架下的纸病图像重构
1.1 CS理论框架
CS理论指出:只要信号本身或在变换域上是稀疏的,便能通过一个与变换基不相干的观测矩阵将其从高维空间投影到低维空间上,这些少量投影包含了信号重构所需的足够信息,便可以通过求解优化问题无失真重构原始信号[7],CS理论的框架如图1所示。

图1 CS理论框图
其具体描述如下:假设一信号
x
∈
R
N×1
在某种基向量
下进行展开,即:

(1)
其中,α=(α1,α2,α3,…,αN)为展开系数向量,Ψ=(Ψ1,Ψ2,Ψ3,…,ΨN)为N×N矩阵,当Ψ为正交基时,有ΨΨT=I。
假设系数向量α只有k(k≪N)个非零值,即α是K-稀疏的,便可以选择一个与正交基Ψ不相关的测量矩阵Φ(M×N,M≪N),对信号x进行压缩测量,即
y=Φx
(2)
能够得到M个线性投影y(M×1),这些少量投影包含了信号重构所需的足够信息[8],测量过程如图2所示。
将式(1)和式(2)合并得到:
y=ΦΨα=ACSα
(3)
当测量值向量y已知时,能够通过测量矩阵Φ和稀疏表示基Ψ实现原信号x的重构[9],信号的重构过程如图3所示。

图3 CS理论信号的重构过程
CS理论包含信号的稀疏表示、测量矩阵的选取和信号的重构算法3个关键技术。信号的稀疏性是CS理论的前提,测量矩阵对稀疏信号进行线性投影,信号的重构算法对原始信号进行重构,压缩感知的重构过程需要对方程y=ACSα进行求解,但方程中y的维数远小于α的维数,因此该方程组为欠定方程组。在CS理论中,只要信号α是稀疏的,通过选择合适的观测方式和重构算法,仅需要K+1次观测,便能将N维空间的K-稀疏信号精确重构[10],其重构过程用式(4)表示:
(4)
CS重构算法一般有两类方法,一种是以基追踪(BasicPursuit,BP)、迭代硬阈值法(IterativeHardThresholding,IHT)和梯度投影法(GradientProjectionforSparseReconstruction,GPSR)为代表的凸松弛算法[11],另一种是以匹配追踪(MatchingPursuit,MP)、正交匹配追踪(OrthogonalMatchingPursuit,OMP)为代表的贪婪算法[12-13]。凸松弛算法重构效果较好,但计算复杂性较高,运算速度慢,难以运用到大规模信号处理的问题中去;贪婪算法虽运算速度快,运算复杂度低,但与凸松弛算法相比,算法精确度相对较低。
1.2BCS-SPL纸病图像重构算法
针对凸松弛算法和贪婪算法不适用于重构二维纸病图像的问题,本研究采用一种SPL算法[14-15],并将其应用到BCS框架中,该算法能够在满足计算效率高的同时实现重构纸病图像质量高的要求。CS理论下纸病图像重构过程如图4所示。
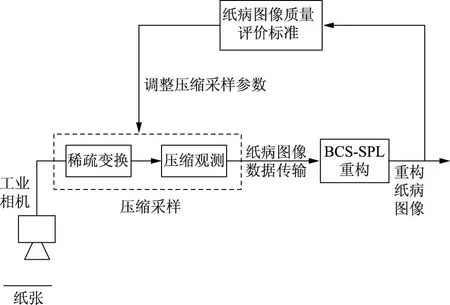
图4 CS理论下的纸病图像重构过程
在BCS中,将一幅大小为N×N的纸病图像分成n个B×B大小的块图像,假设xi表示第i个纸病图像块的向量形式,采用相同的测量矩阵ΦB,对每一块纸病图像进行压缩采样可描述为:
yi=ΦBxi
(5)
对于整幅纸病图像,测量矩阵Φ可表示为对角矩阵:
(6)
由式(6)可知:BCS能够减小测量矩阵的维数,减小随机测量矩阵的存储量,易于传输和存储,具有较好的实时性,但在BCS框架下会使重构纸病图像存在一定的块效应,而SPL算法采用自适应维纳滤波器能够平滑纸病图像中的块效应,因此本研究采用BCS-SPL算法实现纸病的压缩重构过程,其基本思想为:
(1)初始化x(0)=ΦTy。
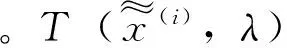
1.3 图像重构质量评价指标
为了在CS理论框架下对重构图像的质量进行评价,本研究从主观标准和客观标准2个方面对重构的纸病图像进行定量描述。客观标准采用峰值信噪比(PSNR),PSNR用信号与噪声的方差之比来估计信号与噪声的功率谱之比,其值越大,重构图像质量越高;主观评价标准为结构相似性指标(SSIM),SSIM从亮度、对比度和结构3方面对图像进行主观评价,其取值范围为[0,1],其值越大,重构图像视觉效果越好。设M×N大小的原始纸病图像和重构后的纸病图像分别为f和f′,则:
(7)
SSIM=l(f,f′)·c(f,f′)·s(f,f′)
(8)
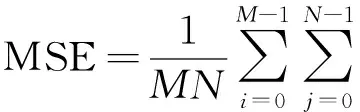
2 基于BCS-SPL重构算法的纸病图像重构实验
为了验证BCS-SPL重构算法对纸病图像的重构效果,本研究将贪婪算法中的OMP算法、凸松弛算法中的GPSR算法的重构效果与BCS-SPL算法的重构效果进行对比。采用PSNR和SSIM作为评价重构图像的客观标准和主观标准,对于计算复杂度,采用重构时间进行度量。
2.1 重构实验
本研究使用如图5所示的块大小为256×256的存在孔洞、污点和裂缝的纸病图像,采用离散余弦变换(DCT)基作为稀疏表示基Ψ。由于高斯随机信号与任意稀疏信号都不相关,采用高斯随机矩阵作为测量矩阵Φ,在采样率分别为0.2、0.3、0.4、0.5下对纸病图像进行分块压缩采样和重构,由于SPL重构算法基于分块压缩感知,将块大小对重构效果的影响进行验证。由于测量矩阵的随机性,所有重构纸病图像的PSNR值、SSIM值以及重构时间均为5次独立实验的平均值。

图5 常见纸病图像

图6 纸病图像在BCS-DCT-SPL时的重构图像

图7 不同采样率的孔洞纸病图像在OMP时的重构图像

图8 不同采样率的孔洞纸病图像在GPSR时的重构图像
由于图像数量较多,文中仅给出BCS-DCT-SPL算法在块大小为16×16、采样率为0.2时的重构纸病图像(如图6所示)。对于孔洞图像,OMP算法和GPSR算法在采样率为0.2、0.3、0.4、0.5时的孔洞重构图像如图7、图8所示。BCS-DCT-SPL算法在块大小为16×16,采样率为0.2、0.3、0.4、0.5时的孔洞重构图像如图9所示。
对不同类型的纸病图像采用BCS-DCT-SPL的重构算法,在不同的采样率、块大小分别为8×8、16×16、32×32时进行纸病图像重构时的PSNR值、SSIM值和重构时间如表1、表2、表3所示。
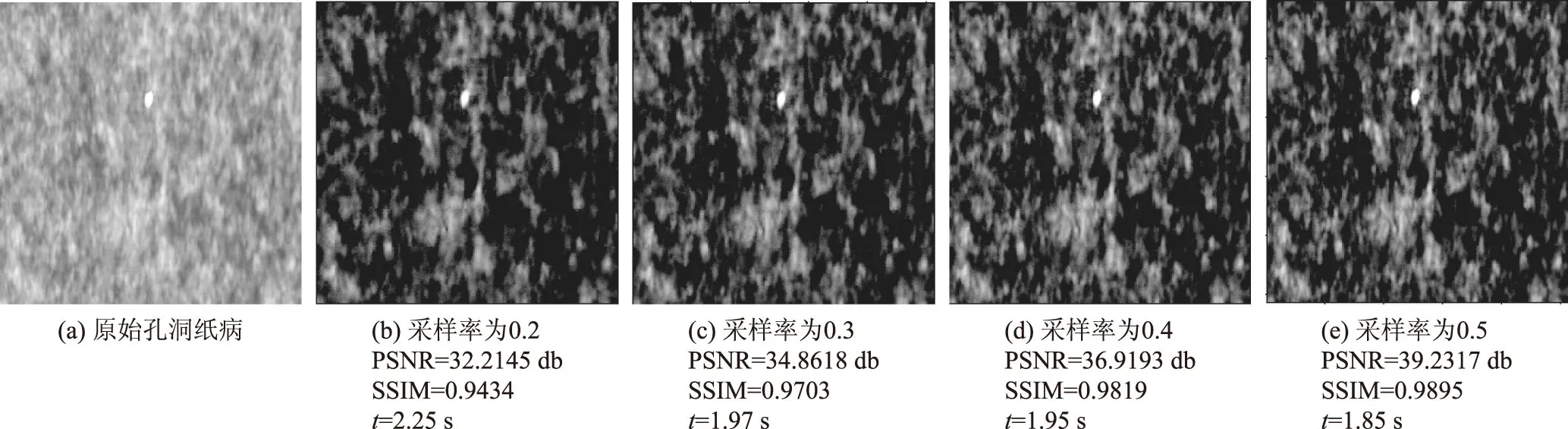
图9 不同采样率的孔洞纸病图像在BCS-DCT-SPL时的重构图像
表1 纸病图像在BCS-DCT-SPL时的PSNR值

db

表2 纸病图像在BCS-DCT-SPL时的SSIM值

表3 纸病图像在BCS-DCT-SPL时的重构时间 s
2.2 重构效果分析
由图7~图9的仿真数据可知:若采用OMP算法对纸病图像进行重构,在采样率为0.2和0.3时不能有效实现对重构图像的主观辨识;若采用GPSR算法,虽然SSIM值和PSNR值相对于OMP算法有所提高,但重构时间大大增加;而BCS-DCT-SPL算法在块大小为16×16、采样率为0.2时即能实现对重构图像的主观辨识。将OMP算法在采样率为0.4时与BCS-DCT-SPL算法在块大小为16×16,采样率为0.2时的重构纸病图像相比较,BCS-DCT-SPL算法比OMP算法重构的纸病图像的PSNR值和SSIM值大,且重构时间更短;在相同采样率下将GPSR算法与BCS-DCT-SPL算法相比,本研究所采用的算法具有更高的PSNR值和SSIM值以及更短的重构时间。通过图7、图8和图9可知,在低采样率下,本研究所采用的BCS-DCT-SPL算法重构的纸病图像具有较高的PSNR值和SSIM值以及较短的重构时间。
3 结 论
本研究根据在当前纸病检测中存在的数据量大、检测速度慢的问题,将压缩感知(CS)理论应用到纸病检测中,采用分块压缩感知(BCS)-平滑投影Landweber(SPL)重构算法对经过压缩的纸病图像进行重构。将峰值信噪比(PSNR)和结构相似性指标(SSIM)作为评判重构图像质量的客观和主观标准,将重构时间作为重构算法计算复杂度的标准,并在不同的采样率和不同的块大小下对孔洞、污点和裂缝纸病图像进行重构仿真。通过仿真结果表明,对原始纸病图像以较低采样率采样,通过BCS-SPL算法重构的纸病图像仍然能够突出纸病特征,保证重构纸病图像的精度,这可以大大减小纸病检测系统的数据传输量,提高系统检测速度,保证了纸病检测系统的实时性。
[1] ZHOU Qiang, WANG Zhi-qiang, YANG Gui-lin, et al. Study of the Realtime Acquisition and Transmission of Paper Disease Image Based on Compressed Sensing[J]. Transactions of China Pulp and Paper, 2015, 30(3): 51. 周 强, 王志强, 杨贵琳, 等. 基于压缩感知技术的纸病图像数据实时采集研究[J]. 中国造纸学报, 2015, 30(3): 51.
[2] ZHOU Qiang, CHEN Ying, SHEN Tian-yu, et al. Review on the Development of Paper Defect Detection System Based on Machine Vision Technology[J]. China Pulp & Paper, 2016, 35(5): 72. 周 强, 陈 颖, 沈天宇, 等. 基于机器视觉的纸病检测系统发展综述[J]. 中国造纸, 2016, 35(5): 72.
[3] JIAO Li-cheng, YANG Shu-yuan, LIU Fang, et al. Development and Prospect of Compressive Sensing[J]. Acta Electronica Sinica, 2011, 39(7): 1651. 焦李成, 杨淑媛, 刘 芳, 等. 压缩感知回顾与展望[J]. 电子学报, 2011, 39(7): 1651.
[4] DAI Qiong-hai, FU Chang-jun, JI Xiang-yang. Research on Compressed Sensing[J]. Chinese Journal of Computers, 2011, 34(3): 425. 戴琼海, 付长军, 季向阳. 压缩感知研究[J]. 计算机学报, 2011, 34(3): 425.
[5] G Lu.Block compressed sensing of natural images[C]//In Proceeding of the International Conference on Digital Signal Processing, Cardiff, UK, 2007: 403.
[6] LI Ran, GAN Zong-liang, CUI Zi-guan, et al. Study Status and Prospective of Compressive Sensing Image Reconstruction[J]. Video Engineering, 2013, 37(19): 7. 李 然, 干宗良, 崔子冠, 等. 压缩感知图像重建算法的研究现状及其展望[J]. 电视技术, 2013, 37(19):7.
[7] JIANG Ye-wen, YU Xin-mei. An Image Variable Sampling and Reconstruction Algorithm Based DWT Multiscale Block Compressed Sensing[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2013, 52 (3): 30. 蒋业文, 于昕梅. 基于DWT的多尺度分块变采样率压缩感知图像重构算法[J]. 中山大学学报(自然科学版), 2013, 52(3): 30.
[8] LI Gai. Research on Reconstruction algorithm in Block Compressive Sensing[D]. Tianjin: Tianjin University, 2013. 栗 改.分块压缩感知重构算法研究[D]. 天津: 天津大学, 2013.
[9] LI Ran, GAN Zong-liang, ZHU Xiu-chang. Smoothed Projected Landweber Image Compressed Sensing Reconstruction Using Hard Thresholding Based on Principal Components Analysis[J]. Journal of Image and Graphics, 2013, 18(5): 504. 李 然, 干宗良, 朱秀昌. 基于PCA硬阈值收缩的平滑投影Landweber图像压缩感知重构[J]. 中国图象图形学报, 2013, 18(5): 504.
[10] Candes E J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transaction on Information Theory, 2006, 52(2): 489.
[11] Mallat S G, Zhang Z F. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397.
[12] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655.
[13] Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1): 129.
[14] Mun S, Fowler J E. Block compressed sensing of images using directional transforms[C]// In Proceedings of the International Conference on Image Processing, Cairo, Egypt, 2009.
[15] Gan L. Block compressed sensing of natural images[C]//Digital Signal Processing, 2007 15th International Conference on IEEE, 2007. CPP
(责任编辑:刘振华)
Paper Disease Image Reconstruction Based on BCS-SPL Algorithm
ZHOU Qiang HU Jiang-tao*WANG Zhi-qiang ZHANG Jun-tao
(CollegeofElectricalandInformationEngineering,ShaanxiUniversityofScienceandTechnology,Xi’an,ShaanxiProvince, 710021)(*E-mail: hujt1020@163.com)
With the growing of the speed and the width of paper machine, the traditional paper disease detection faces the problem of transfering a large number of data and the real-time processing. Compressed sensing theory can effectively reduce the amount of data, but the quality of reconstructed paper disease image is not good when it is applied to two-dimensional paper disease image. In this paper, we used the BCS-SPL reconstruction algorithm to reconstruct the paper disease image, focusing on the reconstruction result of the algorithm under different sampling rates and different block sizes. The experimental results showed that in the compressed sensing framework, the low sampling rate paper disease image reconstructed by BCS-SPL algorithm had high image quality, which could effectively reduce the transmission of paper image data.
compressed sensing; reconstruction algorithm of BCS-SPL; reconstruction of paper disease image
2016- 07-13(修改稿)
周 强先生,博士,教授;主要研究方向:智能信息处理技术,数字图像处理。
TS736+.2
A
10.11980/j.issn.0254- 508X.2016.12.006
*通信作者:胡江涛先生,E-mail:hjt1020@163.com。

