板式换热器单相换热和压降数值模拟

姜未汀, 黄永帅, 韩维哲, 史文斯

(上海电力学院 能源与机械工程学院, 上海 200090)

板式换热器单相换热和压降数值模拟

姜未汀, 黄永帅, 韩维哲, 史文斯

(上海电力学院 能源与机械工程学院, 上海 200090)

建立了板式换热器水侧单流道CFD仿真计算模型,并通过与实验点的对比验证了该模型的精确性.基于数值模拟结果,拟合得到板式换热器水侧换热系数和摩擦因子计算关联式,为板式换热器的优化设计提供了依据.

板式换热器; 单相; 换热; 压降; 数值模拟

随着板式换热器应用领域的不断发展,国内外对板式换热器的研究也趋于多样化.一直以来,国内外对板式换热器水侧换热的研究主要建立在实验的基础上,多是通过搭建板式换热器水-水性能测试实验台研究其水侧换热和压降特性,并通过实验数据拟合得到换热系数和摩擦因子的计算关联式.李晓亮[1]通过实验研究了不同波纹倾角人字形板式换热器的换热性能,并得到板式换热器单相换热和摩擦系数的计算关联式;KHAN T S等人[2]通过实验研究了3种流道下板式换热器水-水单相换热特性,基于实验数据得到努赛尔数经验关联式;AYUB Z H[3]归纳总结了板式换热器水-水单相换热和压降经验关联式.目前,实验研究板式换热器单相换热和压降理论已趋于成熟[4-5],这些实验研究结果为本文提出的以数值模拟研究板式换热器单相换热和压降特性提供了扎实的理论基础和指导.结果表明,利用数值模拟研究板式换热器单相换热和压降特性具有可行性,同时节省了大量的实验时间和经济成本,可以推广应用到基于冷媒的板式换热器两相换热和压降实验研究中.

1 板式换热器单流道数值模型

1.1 数值模型的构建

板式换热器一般由几百张波纹板片组装而成,如果按照实际比例建模,数值计算模型的网格数量巨大,这不仅需要高配置的计算机,而且仿真计算的时间较长,鉴于板式换热器结构的重复性,通道数较多且周期性变化[6],对板式换热器进行数学建模大多采取对板片部分区域进行建模.本文数值模拟的换热器为江苏唯益换热器有限公司生产的B3-095S型钎焊板式换热器,其尺寸参数如表1所示.

表1 板式换热器尺寸参数

本文利用Gambit2.4.6建立了水侧单流道仿真模型,如图1所示.该模型由上下两个板片构成,上下板片之间形成了多个交错的水流道,水由入口流入后,进入下侧两个流道,流至周期性壁面时被折返进入上侧流道,上侧水流至周期性边界时被折进入下侧水流道,以此循环流动,直至从出口流出.

图1 水侧单流道仿真

模型由水侧入口、水侧出口、周期性边界和换热壁面构成,边界条件定义如下:水侧入口采取速度入口边界,入口流速和温度设为恒定,速度方向为垂直于入口表面,并假设入口平面上每个点的速度都相等;板式换热器通道的壁面假设为无滑移边界条件,且壁面温度假设为恒定值;对于周期性平面来说,流体的速度场和压力相等;出口边界条件设定为恒定压力出口.

根据表1构建了B3-095S钎焊板式换热器数值模型,该数值模型水侧入口面积Ain为0.000 0267 32 m2,传热面积Aw为0.001 555 47 m2,模型总长度L为0.047 389 m,当量直径De为0.004 1 m,水的所有物性参数来自Refprop.

1.2 数值模型的验证

相比于实验研究板式换热器水侧换热和压降特性,数值模拟是将板式换热器部分区域进行模型化,由于板片结构的复杂性,构造的数值模型无法完全与实际板片结构相符合,模型仅是换热器内部实际结构的高度理想化.通过数值模拟的方式研究板式换热器换热和压降特性,数值模型的精确程度尤为重要,其决定了模拟结果能否正确反映板式换热器实际换热和压降的性能.为了正确得到板式换热器单相换热和压降性能,本文利用模拟结果与文献[2]中实验点对比的方法验证该数值模型的正确性.

根据文献[2]中的板式换热器结构参数建立了相应的数值模型,并利用Fluent14.0进行模拟计算,CFD模型努赛尔数计算值与文献[2]实验点之间的精度对比如图2所示.由图2可以看出,CFD模型仿真结果与文献[2]实验点具有较高的吻合性,误差在±5﹪以内,这说明提出的单流道CFD仿真模型对于模拟计算板式换热器水侧换热和压降特性是可行有效的.

图2 文献实验值与模型计算值对比

2 数据处理方法

一般在要求不高的湍流条件下,板式换热器整个流程的平均对流换热系数计算式为[7]:

(1)

(2)

(3)

式中:Nu——努赛尔数; hc——换热系数,W/m2·K; De——当量直径,m; λ——导热系数,w/m·k; Re——雷诺数; Pr——普朗特数; C1——待求常数; G——质量流率,kg/s·m2; Cp——比热容,kJ/kg· ℃; μ——粘度,Pa·s.

总换热量为:

(4)

式中:Q——换热量,J; M——质量流量,kg/s; Tin,Tout——进口和出口温度,K.

换热系数为:

(5)

(6)

(7)

(8)

式中:ΔT——对数平均温差,K; Aw——模型传热面积,m2; ΔT1——进口温度与壁面温度差,K; ΔT2——出口温度与壁面温度差,K; Tw——壁面温度,K. 摩擦系数:

(9)

(10)

(11)

式中:f——摩擦系数;ΔP——压降,Pa; Pin,Pout——进口压力和出口压力,Pa; ρ——密度,kg/m3; L——模型长度,m; Ain——模型入口面积,m2.

3 换热系数和摩擦系数关联式拟合

3.1 换热系数关联式拟合

由Fluent14.0计算得到不同入口温度、壁面温度下的计算结果如表2至表5所示.

表2 Tin=290.53,Tw=285.65,Pr=7.51时的计算结果

表3 Tin=282.53,Tw=277.65,Pr=9.60时的计算结果

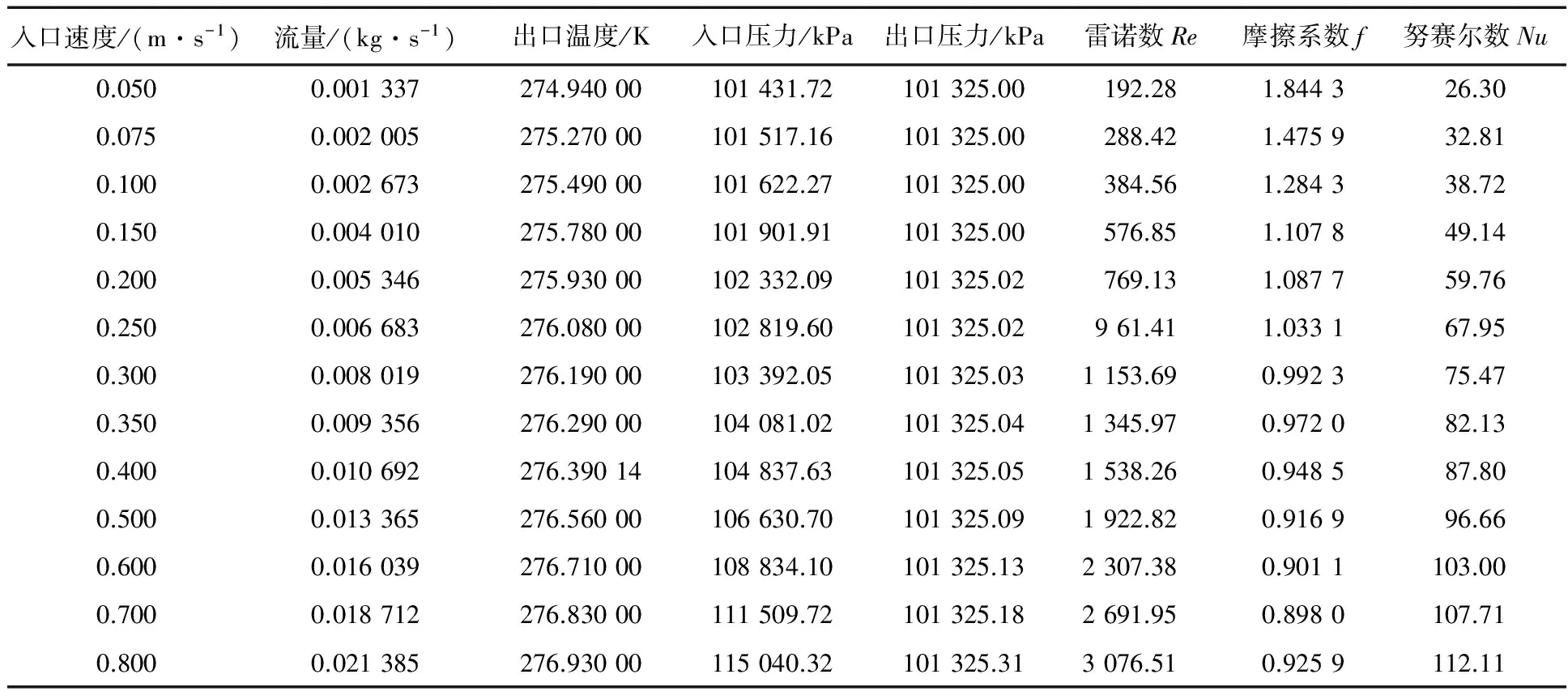
表4 Tin=278.13,Tw=273.25,Pr=11.15时的计算结果

表5 Tin=313.03,Tw=308.15,Pr=4.56时的计算结果

基于计算结果,对式(1)进行回归分析得到板式换热器水侧单相努赛尔数计算关联式:

Nu=1.081 1Re0.518 2Pr0.314 5

130

(12)

模拟结果与关联式计算值之间的精度对比如图3所示.由图3可以看出,两者误差基本在±10%线内,部分误差在±5%线内,仅有少数点误差较大,最大误差为18.86%,平均误差4.48%.

图3 努赛尔数模拟计算值与关联式计算值对比

3.2 摩擦系数关联式拟合

液体在板式换热器中的压降主要来自摩擦阻力,以及角孔压力等,一般摩擦压降计算公式为:

f=C2Ren

(13)

式中:C2——待求常数.

式(13)中,C2和n的数值依据具体的板片结构而定.本文考虑了水的进口速度和进口水温对压降的影响,提出了修正的摩擦系数计算模型:

(14)

基于模拟数据,分别对式(13)和式(14)进行回归分析,得到摩擦系数计算关联式为:

f=5.746Re-0.258 7130

(15)

130

(16)

式(15)和式(16)拟合曲线之间的精度对比如图4所示.

由图4可以看出,由式(16)拟合得到的曲线与数据点之间的吻合度更好,相关性更高,而由式(15)拟合得到的曲线与数据点之间偏离较大,所以本文提出的摩擦系数计算模型更能够体现摩擦系数与雷诺数之间的关系.

摩擦系数模拟结果与式(16)计算值之间的精度对比如图5所示.由图5可以看出,两者误差在±4%线内,最大误差为3.27%,平均误差仅为1.16%.

图4 式(15)和式(16)计算模型拟合结果对比

图5 摩擦系数模拟计算值与关联式计算值对比

4 结 语

本文根据板式换热器单相换热实验研究理论,构建了板式换热器水侧单流道仿真计算模型,通过与实验点的对比验证了该模型的精确性,并利用数值模拟分析了B3-095S钎焊板式换热器水侧单相换热和压降性能.分析结果表明,采取数值模拟研究分析板式换热器水-水换热和压降特性是可行有效的,此数值研究方法可应用于不同型号的系列板式换热器.

[1] 李晓亮.人字形板式换热器强化传热研究及场协同分析[D].济南:山东大学,2009.

[2] KHAN T S,KHAN M S,CHYU M C,etal.Experimental investigation of single phase convective heat transfer coefficient in a corrugated plate heat exchanger for multiple plate configurations[J].Applied Thermal Engineering,2010(30):1 058-1 065.[3] AYUB Z H.Plate heat exchanger literature survey and new heat transfer and pressure drop correlations for refrigerant evaporators[J].Heat Transfer Engineering,2003,24(5):3-16.

[4] MOTA F A S,RAVAGNANI M A S S,CARVALHO E P.Optimal design of plate heat exchangers[J].Applied Thermal Engineering,2014,63(1):33-39.

[5] 杨艳,王英龙.板式换热器设计选型的一种计算方法[J].石油炼制与化工,2004(5):54-56.

[6] 李想.板式换热器传热的数值模拟及波纹板参数优化[D].哈尔滨:哈尔滨工程大学,2013.

[7] 杨崇麟,张明石,王中铮.板式换热器工程设计手册[M].北京:机械工业出版社,1998:45-56.

(编辑 白林雪)

Numerical Simulation of Single-phase Heat Transfer and Pressure Drop in Plate Heat Exchangers

JIANG Weiting, HUANG Yongshuai, HAN Weizhe, SHI Wensi

(SchoolofEnergyandMechanicalEngineering,ShanghaiUniversityofElectricPower,Shanghai200090,China)

A single channel CFD simulation calculation model of a plate heat exchanger is established and the accuracy of the model is verified by comparison with the experimental points.The water side heat transfer coefficient and frictional coefficient calculation correlations of plate heat exchanger are obtained based on the numerical simulation.The correlations provide the basis for the optimization design of plate heat exchanger.

plate heat exchanger; single phase; heat transfer; pressure drop; numerical simulation

10.3969/j.issn.1006-4729.2016.06.003

2015-08-27

简介：黄永帅(1989-),男,在读硕士,江苏徐州人.主要研究方向为板式换热器性能测试与优化设计.E-mail:hys1126795869@126.com.

TK172

A

1006-4729(2016)06-0519-05