在比较中把握知识的本质
李慧敏
[摘 要]数学教学中,教师要抓住教学的重、难点,精心选择比较的素材,巧妙引导学生经历比较的过程,使学生的认识逐步深入,真正理解所学知识。
[关键词]数学教学 比较 本质 图形 放大 缩小
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2016)01-032
比较是确定研究对象共同点和不同点的一种方法,是“一切理解和思维的基础”。下面,我以“图形的放大和缩小”一课教学为例,谈谈如何组织三次比较,引导学生在比较中抓住“变与不变”来认识和理解知识的本质,从而提高学生解决问题的能力和思维能力。
“图形的放大与缩小”是人教版小学数学六年级下册第四单元的内容,教材编排的意图在于使学生认识数学意义上的放大与缩小现象,能利用方格纸将简单图形按一定的比放大或缩小,初步体会图形的相似和几何变换的思想,并渗透“变与不变”的辩证唯物主义观点。
第一次比较:
1.引入放大和缩小
师(实物投影展示):我们可以把字放大或缩小。(板书“放大和缩小”,引导学生体验生活中放大和缩小的现象)
师:这是我们生活中放大和缩小的现象,那么关于生活中的放大和缩小,你还知道什么?(生答略)
师:同学们很善于观察日常生活,说得很精彩。老师也带来了一些生活中放大和缩小的现象,一起看看。(课件出示)
2.揭示课题
(师先通过课件出示一幅很小的图,引发学生产生要放大图才看得清楚的需要,然后用鼠标分别朝横向和纵向拖动两次,使得图片要么放大长,没有放大宽;要么放大宽,没有放大长。这样可引导学生发现这两幅图的大小变了,形状也变了,而第三幅图的大小虽然变了,但形状不变)
师:像这样(课件将原图与放大后的图形去掉画面,抽象出长方形并放入方格图中),平面图形的大小变了,但形状不变,按一定的比进行放大和缩小,在数学上我们称之为图形的放大和缩小。今天,我们就来研究图形放大和缩小的特性。【板书课题:“图形的放大与缩小”】
……
案例分析:
在导入环节中,我在原图的基础上出示了三幅变大后的图,即用鼠标将原图往右、往下和往对角方向分别拖动得到的,因此得到了变长、变扁、形状不变的三幅图。由于特征比较明显,学生很容易在三幅图中找出没有变形的那一幅图,这样就直观地凸显了“放大”的数学本质,使学生明确感受到变大有变形和不变形之分。在此基础上,我再揭示“不改变图形形状的变大,数学上就称为图形的放大”,使学生对图形放大的体会更深刻。因此,课堂教学中,第一次组织学生进行比较活动,意在由生活中通常所说的“放大”自然过渡到数学上的图形“放大”。同时,我借助小方格,帮助学生更好地理解图形放大的数学含义。图形的放大与缩小,较之生活中图形放大与缩小的含义是有差别的。日常生活中,把一个图形的某一条边放大或把某几条边放大都可以笼统地称为图形变大了,但数学上图形的放大是指图形的每一条边按照相同的比放大,且形状不变,其核心要义是形状不变。这样教学,通过学生最熟悉的实物投影和卡通人物的变形图,让他们在课始直接、直观地体会到图形的放大与缩小。
第二次比较:
1.研究图形放大的特性
(1)比较:对比各组汇报的结果,你发现什么变了,什么不变?
(2)交流:同桌交流自己的想法。
(3)汇报:强调每个内角不变,所以图形的形状不变。
师(小结):按一定的比放大后各边的长度变了,周长跟着变了,所以放大后的图形大小变了,但是内角的度数不变,放大后的图形形状也不变。
2.探究图形缩小的特性
(1)自主探究:根据不同的比,把刚才放大后的图形缩小。
(2)独立思考:对比缩小之后和缩小之前的图形,你有什么发现?
(引导学生发现缩小的特性和放大的特性相似)
……
案例分析:
在学生理解的基础上,这一环节安排了有利于学生进行探究、观察、操作、交流的数学活动,使学生初步理解图形的放大和缩小,并获得将图形按一定比进行放大、缩小的经验。然后引导学生通过对比变化前、后图形的各部分数据,重点抓住比较各组图形长、宽、周长、角的大小之间变与不变的关系,突出形状不变的数学本质。
教师教学用书中明确指出:“教学‘图形的放大与缩小’时,应引导学生比较它们的内角、边长、周长,思考‘什么变了,什么没变’,使学生能有目的地深入观察、对比和思考。”我们知道,数学意义上对图形的放大与缩小的界定,是放大与缩小前后形状不变,但教材中没有明确地给出形状不变的术语,而是用图形举例。如教材P60中列举了三个图形,值得注意的是,出示的顺序是正方形、长方形、三角形。这样的编排顺序目的是先用正方形和长方形举例,因为这两个图形的四个角都是直角,使学生直观感受内角不变的情况(即“保角变换”),然后在三角形的探究中,通过量角进一步说明内角不变。最后,通过对应边的关系比较,得出对应边的比(即相似比)相同,这就是数学意义上图形的放大与缩小(即图形相似)。这样数学,把形状不变蕴含在举例和比较的过程中,符合小学生的认知规律。
第三次比较:
(师出示练习,如下):
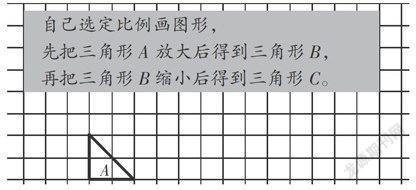
生1:2∶1、3∶1都表示放大,那么1.5∶1可以吗?
生2:当比为1∶1时表示什么?
生3:1∶4、1∶6表示缩小,那么还有什么样的比表示缩小?
师(追问):比较刚才我们在黑板上记录的所有的比,你发现了什么?
……
案例分析:
这是全课的综合性训练,即把所有的比一一列举出来进行比较,便于学生发现规律,清楚地认识到放大的比和缩小的比有什么特点,真正理解比所表示的具体含义。可以说,第三次比较是课堂教学中的画龙点睛之笔。
有比较才有鉴别,有鉴别才容易揭示规律、把握本质。在数学教学中,教师要抓住教学的重、难点,精心选择比较的素材,巧妙引导学生经历比较的过程,使学生的认识逐步深入,真正把握知识的本质,获得不同的发展。
(责编 杜 华)

