数量化理论Ⅰ在职业院校课程设置中的应用

吴　迪

(吉林化工学院 教务处，吉林 吉林 132102)



数量化理论Ⅰ在职业院校课程设置中的应用

吴迪

(吉林化工学院 教务处，吉林 吉林 132102)

摘要：应用数量化理论Ⅰ，以学生的各科成绩为依据，寻找文化素质课与职业能力的内在关系，并对构建课程体系及课程设置的合理性及科学性等方面进行分析与评价.

关键词：数量化理论；典型相关分析；典型变量；相关系数

高职教育的主要任务是培养高技能人才.高技能人才应具备的知识、能力、素质是教育理论研究中的常见话题，对三者的内涵、相互关系做何种解读，直接影响着教育实践的走向.由于各学校对三者的相互关系在理解上存在差异，导致了在课程体系设计、课程设置上做法不一，有的提倡“知识本位”采用以传授知识为主的教学模式，有的“轻文化、重技能”采用“师傅带徒弟”的教学模式，忽视文化课教学的倾向[1-2].本文应用数量化理论Ⅰ，寻找知识、能力、素质三者的相互关系，为构建符合“高技能人才”内涵要求的课程体系、课程设置提供理论依据[3-4].

数量化理论是多元分析的一个分支.数量化理论Ⅰ与回归分析、典型相关分析都是对定量基准变量的预测和发现，前者主要研究定性变量，后者主要研究定量变量.

高职教育的课程一般分为公共基础课、专业基础课、专业课、实训课程、顶岗实习和素质教育.我们设定文化素质和职业能力两个项目，分别用变量U、V表示，文化素质项目设人文素质、数学、语文3个类目，并分别用x1、x2、x3表示，人文素质包括军训、社交礼仪、心理健康、演讲与口才等任选课.职业能力项目设职业基础、专业能力、综合能力3个类目，并分别用y1、y2、y3表示，职业基础是指专业基础理论知识，专业能力是指从事某种职业的能力，主要由专业理论课、实习、实训成绩构成，综合能力是指跨职业的专业能力、方法能力、社会能力、个人能力，具体体现是顶岗实习成绩.考虑变量U、V与x1、x2、x3、 y1、y2、y3之间的线性组合.

U=a1x1+a2x2+a3x3

(1)

V=b1y1+b2y2+b3y3

(2)

在所有可能的线性组合中，寻找一对相关系数最大的线性组合，用这对线性组合的相关系数ρ(UV)表示这两组变量的相关性，叫做两组变量的典型相关系数，而这两个线性组合叫做一对典型变量，从而求得文化素质与职业能力之间的相关关系.由于篇幅有限，这里仅给出应用计算实例，对其方法原理及理论推导，在此不作赘述.

1应用计算实例

1.1　数据的转换利用

在机械制造专业的学生中随机抽取44名作为样品，考察其文化素质与职业能力所包含的各科成绩.这些成绩中有定量的：如数学，而有些是定性的：如军训分为优、良、中、差四个等级，对于定性数据转换成有序型数据，如成绩优取95分，良取85分、中取75分、差取65分.这些数据不表示任何比例关系，仅表示等级的差异.将定量及转换后的定性数据进行中心化处理[3-6].

1.2　计算协方差阵及相关阵

由中心化处理得到的数据构成原始数据矩阵为：

Z=[XY]

其中X为文化素质的三个变量所构成的矩阵，Y为职业能力的三个变量所构成的矩阵.

利用Z，可计算协方差矩阵并将其分块.

其中

同时，计算相关矩阵如下：

1.3　问题的求解

根据求条件极值的拉格朗日不定乘数法则，对于典型相关分析问题，最后可得到如下方程组：

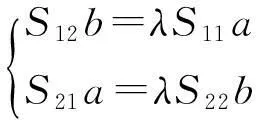
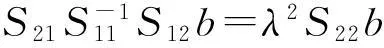
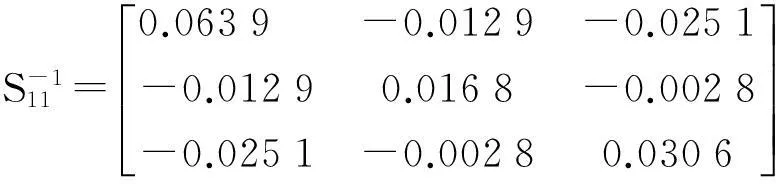
设 t=λ2得

t3-1.0113 3t2+0160053t-0.004 0=0,

其特征值为：

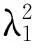
于是典型相关系数为

λ1=0.907 0,λ2=0.397 2,λ3=0.175 5.

相应的特征向量为

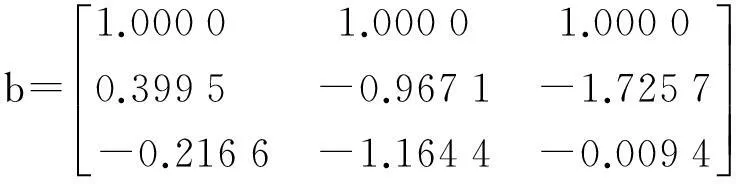
同时可求得：

1.4　典型相关系数的显著性检验[5]

前面所引进的原始数据矩阵X实质上是3维随机向量的容量为44的样本值，Y也是一个3维随机向量的容量为44的样本值，所得到的中间结果和最后结果都是母体的相应结果的估计值，因此，有必要对各典型相关系数在一定的显著性水平α=0.025下作X2检验.

我们对典型相关系数作X2检验，构造统计量为：

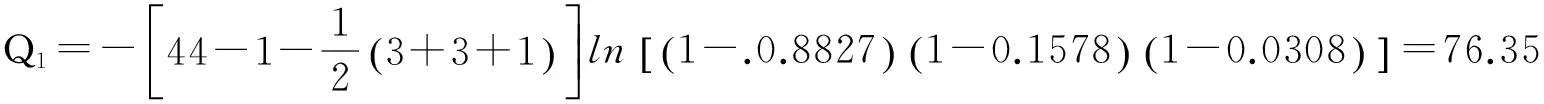
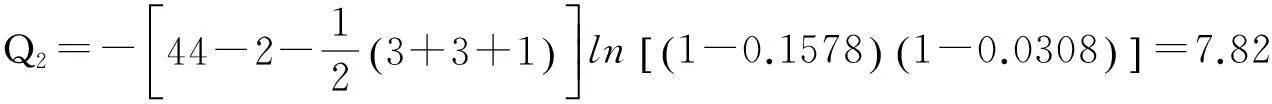
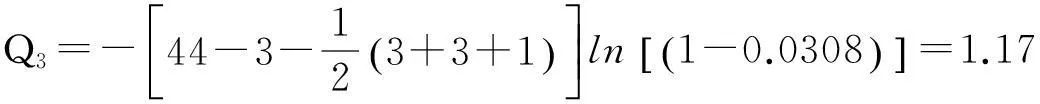
查自由度为3×3=9、(3-1)×(3-1)=4、(3-2)×(3-2)=1的X2分布表，相应于α=0.025的水平下，临界值分别为19.02、11.14、5.02.

可见在α=0.025的水平下，第一对典型相关系数是显著的，第二、第三个典型相关系数是不显著的，于是用第1对典型相关变量表示两组变量的相关性.

1.5　结论

根据前面计算结果，我们可用第一个典型相关系数所对应的ab将典型变量的线性组合表示如下：

U=0.8379x1+0.4709x2+0.3829x3,

V=y1+0.3995y2-0.2166y3,

其相关系数ρ(UV)=0.907 0

2计算结果的分析

根据应用计算实例的结果，我们对以下四个方面问题进行分析讨论[8].

2.1　典型相关系数

最终计算结果表明，文化素质U与职业能力V和各变量x1、x2、x3、 y1、y2、y3可用线性组合的形式建立方程组为：

U=0.8379x1+0.4709x2+0.3829x3,

V=y1+0.3995y2-0.2166y3,

典型变量U和V之间的相关系数ρ(UV)=0.907 0.这说明文化素质与职业能力之间存在较高的相关性.

随着产业结构的调整，科学技术的发展，职业能力的外延与内涵也发生了很大变化.对于企业及企业员工来说都要求具有及时掌握特定职业在职场中的发展趋势和最新动态的能力；自主学习新的职业技能的能力；掌握最先进的相关职业理念和操作方法的能力；扩大知识面，形成更全面的具有延伸性知识结构的能力.这样才能使学生不仅能够成功就业，而且在必要时能顺利转岗或再就业，甚至赢得更新更好的职位.

从理论和实际两个方面上来说文化素质的培养，对提高学生的职业能力有着极其重要的作用.

2.2　利用典型变量UV的线性组合进行预测估计

将作为样品的每名学生在变量x1、x2、x3、 y1、y2、y3上取值代入所建立的方程组中，可得到学生文化素质与职业能力的量值，这个量值反映了一名学生的文化素质水平与职业能力的估计值，如果我们把所有学生在变量x1、x2、x3、 y1、y2、y3的取值代入所建立的方程组中，就可以得到全部学生表示文化素质水平与职业能力的量值.根据这些量值的大小，我们可以确定学生之间文化质素与职业能力之间的相对高低差异.

因为文化质素与职业能力存在较高的相关性，我们可以用一组变量的线性组合的数值去预测另一组变量的某线性组合的数值.就是说，除了特殊的例子外，如果某个学员的文化质素较高，我们就可以预测该学员的职业能力也不会太差.如第10号样品文化素质的取值为19.6，职业能力的取值为18.69，其文化素质的取值较高，职业能力的取值也相应较高.第三十样品文化素质的取值为-10.47，职业能力的取值为-11.34中，其文化素质的取值较低，职业能力的取值也相应用较低.在作为样品的四十四名学员中有四例除外，其余都符合了以上规律.

2.3　相关矩阵

从相关矩阵，我们可以得到各变量(课程)之间的相关关系，以便对我们课程设置的合理性及科学性作出客观的评价.

(1) 从相关矩阵我们可以看出人文素质与数学、语文、职业基础、专业能力的相关系数大于0.5，人文素质与科学知识、操作技能有如此高的相关关系，说明素质教育与全面发展教育从根本上说具有一致性.全面教育就是使学生的学业、身心、人格和谐的发展，不能只信奉“知识就是力量”，而在一定情况下，“品德与人格更是力量”.因些课程设置和教学应与培养目标相适应，不仅传授知识和技能，也要注重学生品德素质的培养，注重学生人格的塑造.使学生成为有理想、有道德、有文化、有纪律的一代新人.

(2) 从相关矩阵我们可以看出数学与职业基础、专业能力的相关系数大于0.5，说明数学与职业基础、专业能力有一定的相关关系.数学主要培养学生的逻辑推理能力、空间想象能力、计算能力，这些能力为学习专业基础课、专业课奠定了基础，如数控编程中的坐标平移、公差中的数值计算、机械制图中的空间想象等.同时我们还看到职业基础与专业能力的相关系数为0.89，两者呈高相关，说明职业基础课程中的机械制图、极限配合及技术测量、机械设计基础等课程的重要性，如果不会看图、不懂加工精度要求、材料特性，就不可能加工出合格的零件.这样的解释是合情合理的,因此说明我们的课程设置基本是合理的.

(3) 从相关矩阵我们可以看出数学与综合能力、专业能力与综合能力之间呈低相关(相关系数小于0.4)，这说明数学与职业能力、专业能力与职业能力之间尽管存在某些联系，但彼此之间有较强的独立性.例如专业能力与综合能力的系数为0.37，低于0.4，说明综合能力不是老师在课堂上教出来的、学生学出来的，而是学生在工作岗位练出来的、做出来的.这也就说明了 “2+1”培养模式的合理性.

2.4　载荷

典型变量UV可以用变量x1、x2、x3、 y1、y2、y3的线性组合的形式表式，变量x1、x2、x3、 y1、y2、y3的系数称作为该变量的载荷.典型变量的意义主要由那些载荷较高的变量所决定.

在文化素质U的线性组合中，变量x1、x2、x3的载荷并无显著差异，这说明构成文化素质的三个变量所起的作用几乎相等.

在职业能力V的线性组合中，变量y1的载荷明显地大于y2、y3的载荷，这说明在构成职业能力的三个变量中，职业基础起着较为重要的作用.

以上分析，可为学校的课时安排提供科学的依据.

3结束语

数量化理论是正在发展着的理论，随着计算机技术的发展，近几年这一理论在国内外地质、林业、气象、环境保护、经济、医学等领域得到广泛的应用.将数量化理论引入教学设计与课程设计评价还处于开发实验阶段，因此，尚有不少问题值得研究和探讨，如类目的如何划分、定量数据转化为定性数据对结果有什么影响等等，这些问题都有待于在理论与实践两方面来解决..

参考文献：

[1]陈冬松.地方工科院校高等职业教育人才培养模式研究与探索[J].吉林化工学院学报，2015，32(9)：55-58.

[2]史礼娜.高等职业技术教育在科技成果产业化中的作用研究[J].吉林化工学院学报，2014，31(2)：70-72.

[3]董文泉.数量化理论及其应用[M].长春：吉林人民出版社，1979.

[4]祝东进，郭大伟.概率论与数理统计[M].北京：国防工业出，2010.

[5]冯娟.地方院校数学专业基础课与专业课关系的量化分析[EB/OL].http://www.cqvip.com/read/read.aspxid=30915838#.2009.6.

[6]曹俊,刘莉莎.专业基础课和实训课程间的典型相关分析[EB/OL].http://www.chinaqking.com/%D4%AD%B4%B4%D7%F7%C6%B7/2009/59578.html.2009.11.

[7]傅德印.典型相关分析中的统计检验问题[EB/OL].http://www.docin.com/p-165933587.html.2008.7.

[8]机械类专业基础课与专业课相关性的量化分析[EB/OL].http://www.doc88.com/p-1864679932 252.html.2011.5.

The Application of Qauntity Theory in the Cirriculum

of Vacational Education

WU Di

(Office of Academic Affairs,Jilin Institute of Chemical Technology,Jilin City 132022,China)

Abstract:This text is to research the intrinsic correlations between cultural quality courses and vocational capability using quantity theory which is based on study achievements.Also,the reasonableness and correctness of the course system's framework have been analyzed and evaluated.

Key words:quantity theory；typical correlative analysis；typical variable；correlative coefficient are earth

文章编号：1007-2853(2015)11-0094-04

作者简介：王燕飞(1981-)，女，吉林省吉林市人，吉林化工学院讲师,博士，主要从事统计决策及试验设计方面的研究.

收稿日期：2015-07-04

中图分类号：O 212

文献标志码：A DOI：10.16039/j.cnki.cn22-1249.2015.11.023