管道机器人的驱动单元工艺优化设计

王　月，钟梓楠* ，吕金贺

(1.北华大学 机械工程学院,吉林 吉林 132013;2.北华大学 汽车与建筑工程学院,吉林 吉林 132013)



管道机器人的驱动单元工艺优化设计

王月1，钟梓楠1*，吕金贺2

(1.北华大学 机械工程学院,吉林 吉林 132013;2.北华大学 汽车与建筑工程学院,吉林 吉林 132013)

摘要：驱动单元的驱动特性和可靠性决定管道机器人的工作效率及其工作能力，由于对管道机器人三轴差速驱动单元的优化大部分都由电脑仿真来完成，但是在制造、装配阶段还是会导致差速不准、功率过大等问题.因此本文通过对三轴差速器工艺的优化，解决了工艺当中的公差分配问题，降低了零件的工艺难度，建立了十字轴垂直度误差对啮合质量和轴向调正间隙的函数关系.

关键词：管道机器人；三轴差速器；传动精度；工艺优化

管道机器人用于工作在管道内部特定的空间里的智能装备，用来完成管内加工、异物清除、防腐涂层的涂敷、管道缺陷检测等任务，从管道机器人出现至今，已经有多项研究成果[1-4].而在众多研究中，为了保证机器人能够长距离巡线，对管道机器人提出了如下性能要求：①环境适应性好；②驱动效率高；③结构紧凑，功率体积比大；④移动速度快；⑤系统运行可靠性高.

在前期研究过程中，通过对三轴差速驱动单元的仿真分析可知，只要所设计的驱动单元结构对称就可以保证实现差速功能，但是由于设计、制造和装配调整不当，还是可能会出现差速不准和功率消耗过大等故障.本文将从工艺优化的角度出发，以提高传动精度为目标，对典型零件和结构进行工艺优化分析，解决了工艺当中的公差分配问题，降低了零件的工艺难度，建立了十字轴垂直度误差对啮合质量和轴向调正间隙的函数关系[5-6].

1三轴差动式驱动单元的结构与机构原理

管道机器人三轴差动式驱动单元由驱动部分和压紧力调节部分组成.驱动部分由驱动电机驱动三轴差速机构，并由三轴差速机构并联驱动沿周向120°均布的3个锥齿轮副，锥齿轮又通过同步带带动驱动单元的前行走轮组运动，前行走轮组经由同步带把运动传递到后驱动轮组，从而实现驱动单元由一个电机驱动，三路差动输出的目标.压紧力调节部分由预紧滑套、支撑杆及平行四杆式驱动轮支架等组成.通过电机驱动，调节弹簧的预压缩量来调节驱动轮与管壁的接触压力，从而使驱动单元获得足够的拖动力，且驱动单元可适应一定范围的管径变化[7-9].三轴差动式管道机器人驱动单元虚拟样机如图1所示.

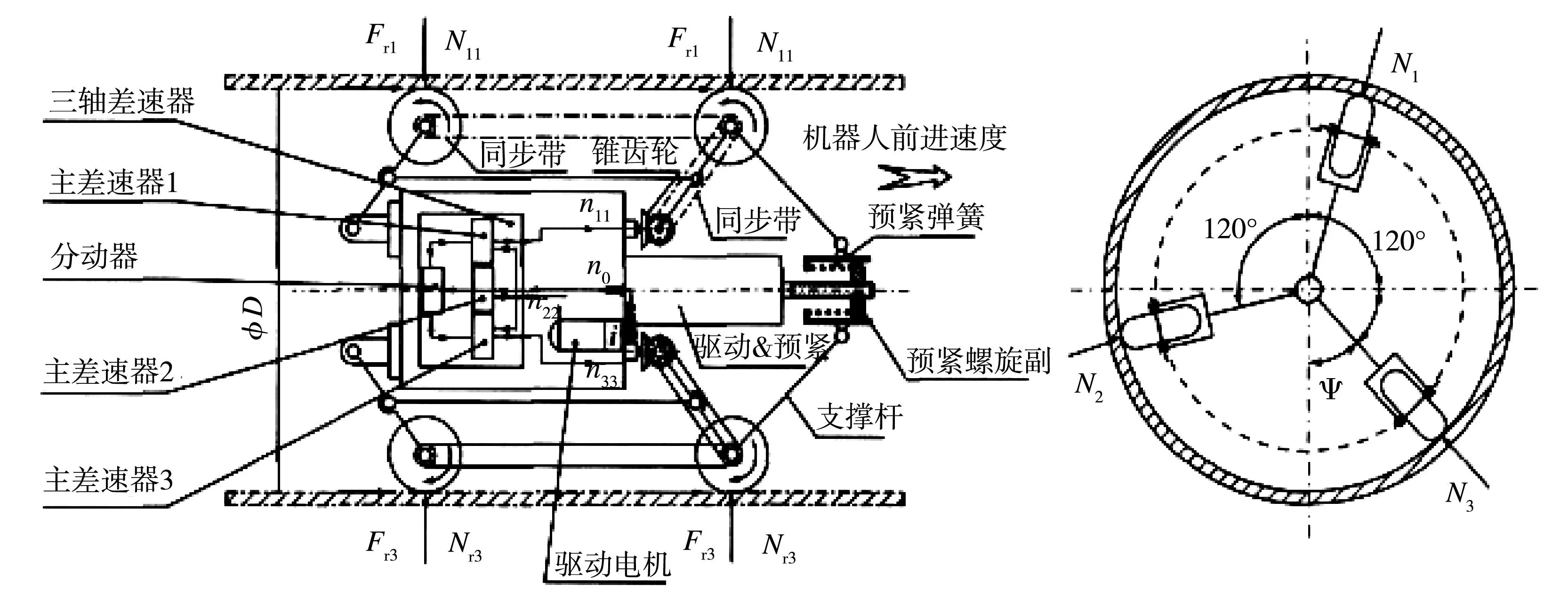
图1　三轴差动式驱动单元结构原理图

2驱动单元的三轴差速机构及其差速特性

2.1　三轴差动式驱动单元的差速机构

如图2所示，三轴差速机构是由主差速器1、主差速器2、主差速器3及分动器等4个差动轮系组成，具有由单个输入运动n0转化成三路差速输出nii(i=1,2,3)的功能[10-12].

图2　三轴差动式驱动单元的差速机构

2.2　三轴差动式驱动单元的差速特性

2.2.1三轴差动式驱动单元在直管阶段的差速方程

管道机器人驱动单元在直管内运动时，三轴差速器不差速，驱动单元在管内作平动，各行走轮在纯滚动状态下，所有的轮心速度应当一致，且轮心的速度应当等于行走轮的半径与其旋转速度的乘积[11].故满足如下运动方程：

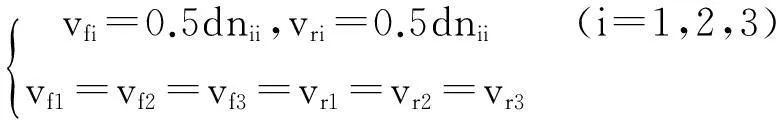
(1)

由方程(1)，可确定驱动单元在直管阶段各行走轮的转速.

2.2.2三轴差动式驱动单元在弯管阶段的差速方程

图2所示为驱动单元在弯管阶段的差速原理，由于管道机器人自身对称性的特点，前行走轮组轮心所确定的管道截面图形与后行走轮组轮心所确定的管道截面图形是完全相同的，对应的前后行走轮的速度也必然是相等的，

vfi=Rfiω=vri=Rriω=0.5dnii

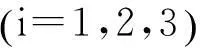
因此有：

(2)

vf1:vf2:vf3=Rf1:Rf2:Rf3=n11:n22:n33

(3)

vr1:vr2:vr3=Rr1:Rr2:Rr3

(4)

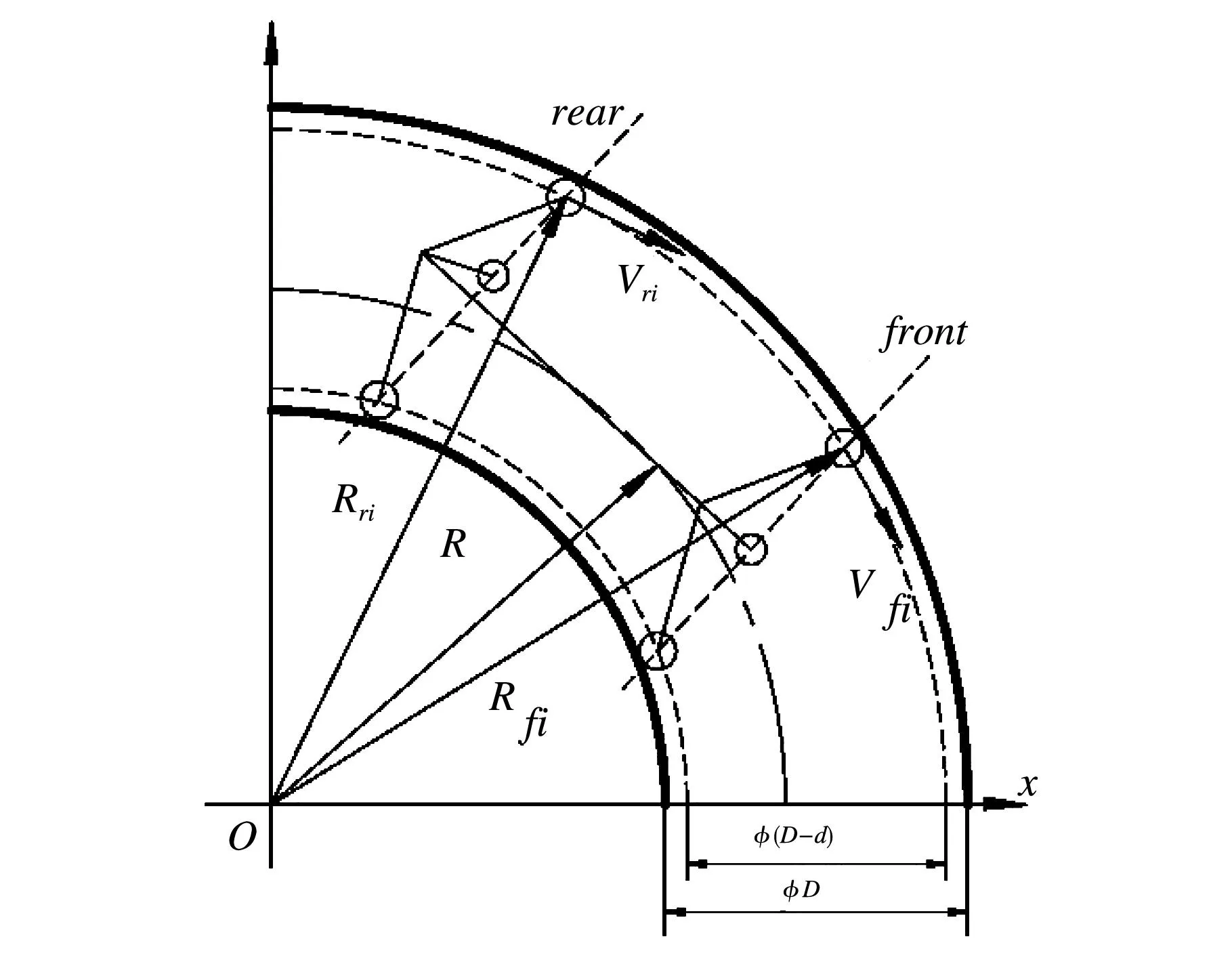
图3　驱动单元弯管阶段差速原理

3三轴差速器零件及工艺进行优化

3.1　驱动单元支撑板孔系加工中的工艺优化设计

计算平面尺寸链的常用方法有：卡具法、投影法和极值法，但是这些方法很难应用于几个互相成一定角度的工艺尺寸，特别是含有角度公差的情况.在三轴差动式驱动单元试制过程中，有三件形状类似的零件，对前支撑板为孔系进行计算发现，上述方法分配的公差值都不近合理，要么浪费了工艺能力，要么出现工艺能力不足等情况，而采用偏微分方程导出的多元函数微分学公式，使用起来方便有效，满足了工艺要求.

以中心轮的中心B为坐标原点建立参考坐标系，电动机上的主驱动轮中心A和行星轮中心C的坐标值如图所示，不必进行计算即可得知.现在只要计算出另外两个行星轮的中心点D和E的坐标值及公差值就可以解决加工中的工艺问题.

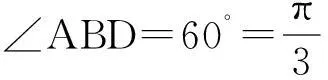
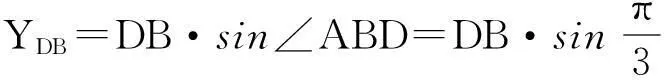
(5)

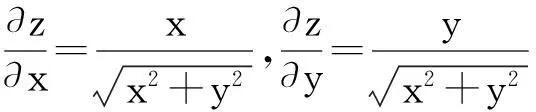
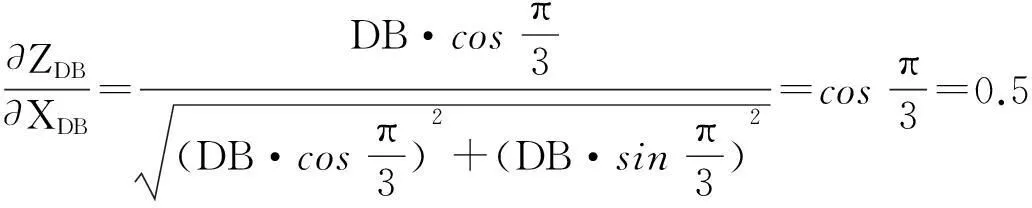
(6)

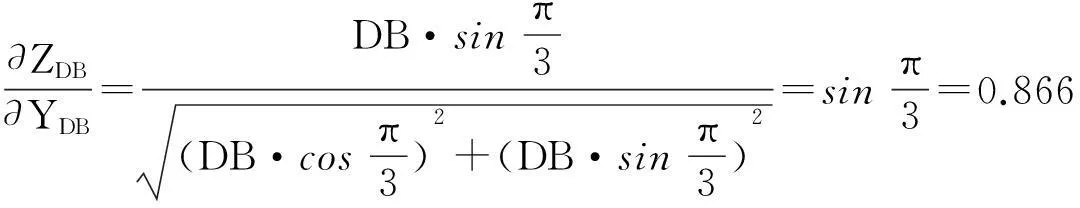
(7)

故得

(8)

由于采用了等公差原则，所以把两者取成一致并向小值方向圆整.所以取：δx=δy=±0.014

(2) 验算

(3) 重新验算

上述计算的结果虽然不合理，但是相差甚微，为了保障有足够的工艺能力，需要进行重新验算，故令δx=δy=±0.013

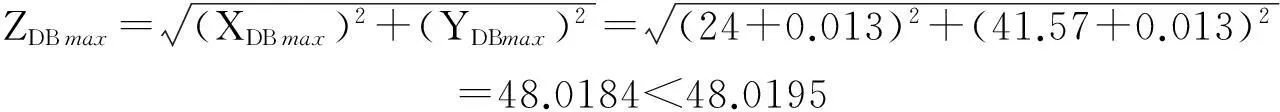
以上的计算结果表明：

XDB=24±0.013，YDB=41.57±0.013.

(9)

计算的结果可以应用到数控铣床或坐标镗床上，也可以用在有数显装置的铣床或普通铣床上，均可以保证加工的精度要求.采用同样的方法可以求出E点的坐标值和相应的公差值，计算过程略.

经过上述理论计算及实际应用可知，把偏微分方法引入到三轴差速驱动单元支撑板的孔系加工工艺计算中，各个纵横坐标的偏差分配合理，可以把精度要求较高的零件从高精度机床上移至普通机床上进行加工，拓宽了机床的工艺能力，发挥了其潜在的经济效益，降低了科研开发的周期和成本，此计算方法同样可以应用到其它类似的孔系零件加工.

3.2　驱动单元装配中的工艺优化设计

如图4所示，正常啮合时4个圆锥齿轮1、2、3和4的分度圆锥对称于x与y坐标轴，当十字轴存在垂直度误差时，分度圆锥则对称于坐标原点O，圆锥齿轮1和2之间的分度圆锥位置间的距离即为a1e1和a1j1直线之间的距离，最小值在a1点，最大值为e1和j1之间的距离.a1点的坐标为：

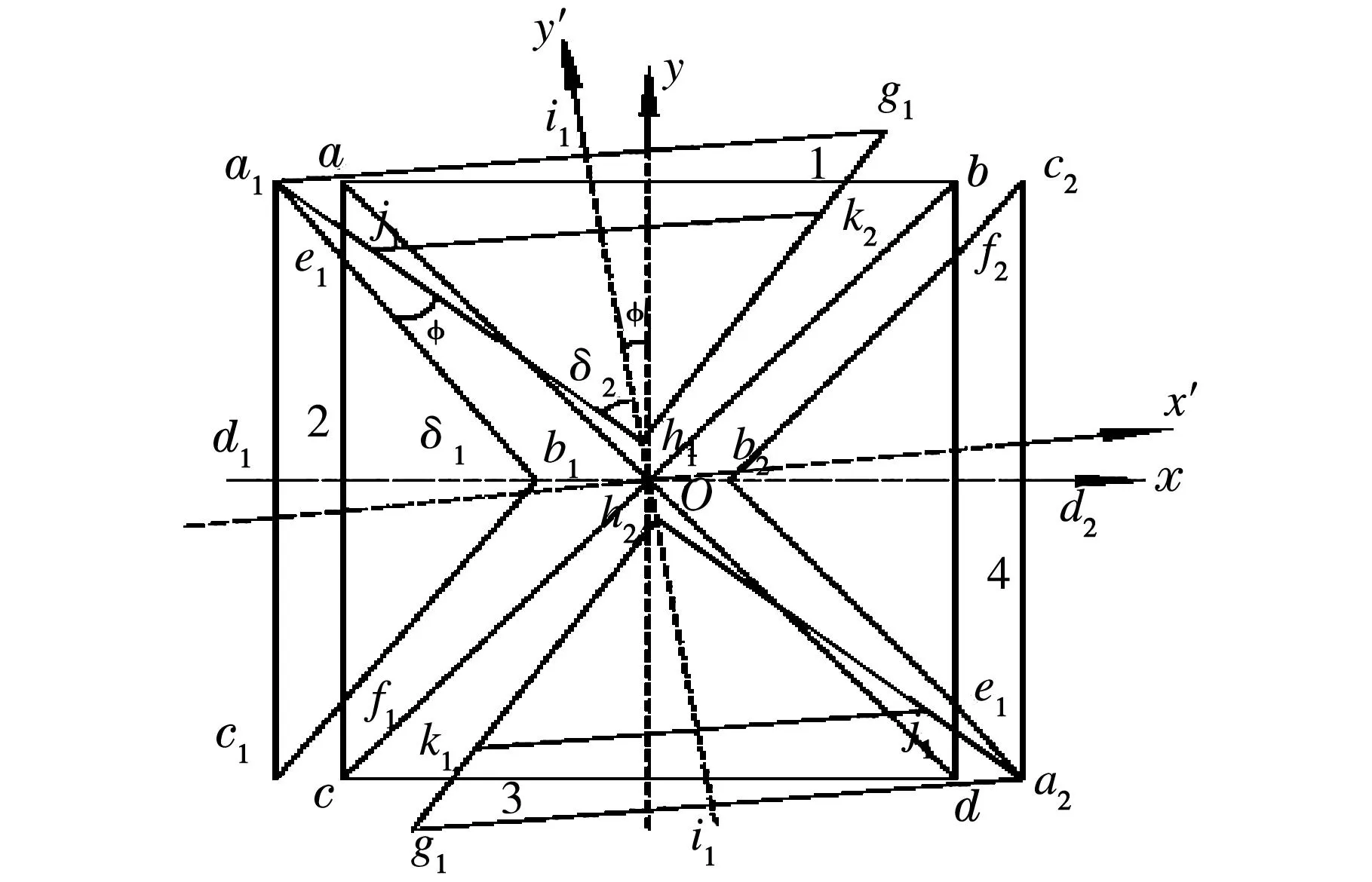
图4　分动器机构十字轴垂直度误差分析简图

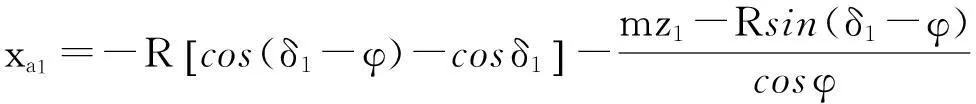
由图4可见，圆锥齿轮1和2之间的分度圆锥在此处重合，其位置间的距离为零.e1点的坐标为：

j1点的坐标为：

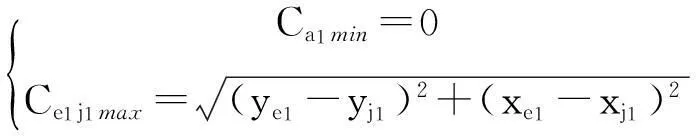
(10)

圆锥齿轮1和4之间的分度圆锥位置间的距离即为g1k1和c2f2直线之间的距离，最大值为g1和c2之间的距离，最小值为k1和f2之间的距离.

g1点的坐标为：

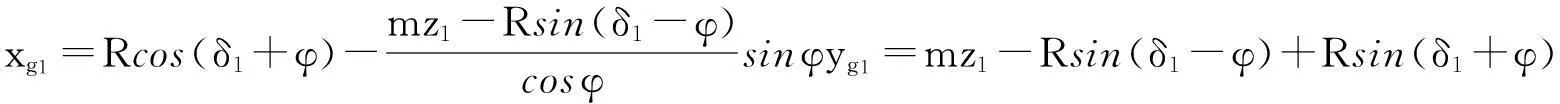
c2点的坐标为：

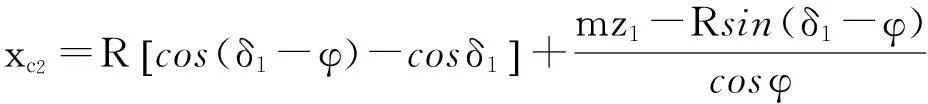
yc2=Rsinδ1

k1点的坐标为：

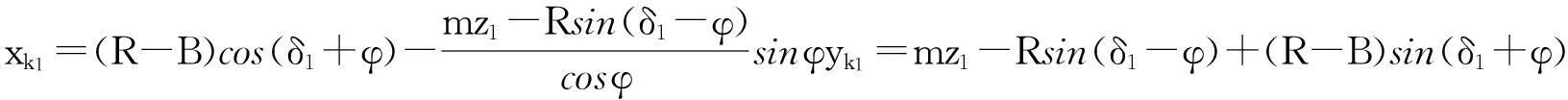
f2点的坐标为：

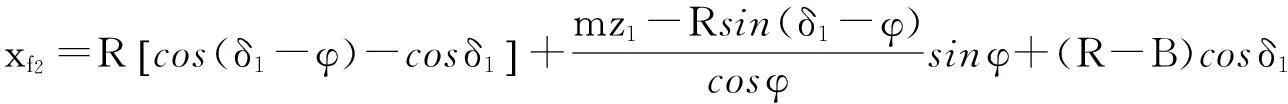
yf2=(R-B)sinδ1

则：圆锥齿轮1和3之间的齿顶隙变化量

(11)

由图4可以看出圆锥齿轮2和3之间的分度圆锥位置间的距离变化量与圆锥齿轮1和4之间的距离变化量相同，圆锥齿轮3和4之间的分度圆锥位置间的距离变化量与圆锥齿轮1和2之间的分度圆锥位置间的距离变化量也相同，且它们之间是对称于坐标原点的.

从上述的分析结果可以看出，当十字轴存在垂直度误差时即影响圆锥齿轮副的啮合质量又影响装配时的轴向调正间隙，所以在设计与加工装配中应当根据实际情况选用合理的形位公差，并且在采用有效的加工工艺，这样才能保证装配质量，直至保证差动机构的传动精度.

4结论

通过对三轴差动机构中的支撑板和十字轴组件进行工艺优化分析，解决了如下问题：

(1) 用偏微分法解决了工艺当中的公差分配问题，降低了零件的工艺难度，这样即使是在普通机床上也能保证零件的加工质量，节约了科研经费，减少了加工周期.

(2) 系统详细地分析了十字轴存在垂直度误差时对圆锥齿轮副的啮合质量和装配时的轴向调正间隙的影响，建立了十字轴垂直度误差对啮合质量和轴向调正间隙的函数关系，在可靠性分析中能够定量分析管道机器人三轴差动式驱动单元传动精度.

参考文献：

[1]Shuxiang Guo and Yasuhiro Sasahi.A New Kind of Microrobot in Pipe Using Driving Fin[J].Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics,2003:697-702.

[2]Shuxiang Guo.A New Type of Microrobot for Biomedical Application[J].Proceedings of the 2004 IEEE/ASME International Conference on Advanced Intelligent Mechatronics,2004:867-872.

[3]杨斌久,姜生元,耿德旭,等.三轴差速器的设计及应用[J].吉林大学学报:工学版,2002,32(4):70-75.

[4]张玉峰，姜生元，李建永，等.介质流压差驱动式管道机器人的驱动、调速原理分析及结构设计[J].吉林化工学院学报，2009,26(2):85-88.

[5]张学文,贾亚洲,邓宗全,等.管道机器人三轴差动式驱动单元的设计研究[J].机器人,2008,30(1):22-28.

[6]卢伟宏，王海波，孟庆鑫.一种教学机器人控制系统研发[J].吉林化工学院学报，2009,26(4):67-69.

[7]唐德威,梁涛,姜生元,等.机械自适应管道机器人的机构原理与仿真分析[J].机器人,2008,30(1):29-33.

[8]张学文,贾亚洲,姜生元,等.管内移动机器人三轴差动单元可靠性分析[J].吉林大学学报:工学版,2008,38(2):365-369.

[9]汤婷洁,李朝东.微型管道机器人及其电驱动技术[J].微特电机,2005(4):36-38.

[10] 朱敬德,周明,应金贵,曾俊冬.在役石油管道检测机器人机械设计[J].上海大学学报(自然科学版),2001,7(1):57-59.

[11] Riggins R,Snider J,Mutter B.Design and analysis of an autonomous ground robotic vehicle[J].AUVSI's Unmanned Systems North America,2004-Proceedings:295-309.

[12] Korayem M.H,Rostam T.Bani,Nakhai A.Design,modeling and errors measurement of wheeled mobile robots[J].International Journal of Advanced Manufacturing Technology,2006,28(3-4):403-416.

Pipeline Robot Drive Unit Process Optimization Design

WANG Yue1,ZHONG Zi-nan1*,LV Jin-he2

(1.College of Mechanical Engineering,Beihua University,jilin City 132013,China;2.College of Automotive and Architectural Engineering,Beihua University,Jilin City 132013,China)

Abstract:The driving characteristics and reliability of the drive unit determine the working efficiency of the pipeline robot and its working ability,as a result of the optimization of pipeline robot tri-axial differential drive unit mostly are done by computer simulation,but in the manufacturing and assembly phase will lead to inaccurate differential,too much power.So in this paper,through optimizing the tri-axial differential technology,solving the problem of tolerance allocation among technology,reducing the parts of the technology difficulty,cross axis perpendicularity error on the meshing quality and a function of the axial adjustment clearance is established.

Key words:pipeline robot；tri-axial differential；transmission accuracy；process optimization

文章编号：1007-2853(2015)11-0050-05

通信作者：*曹亮，E-mail:caoliang@cust.edu.cn

作者简介：关会英(1980-)，女，吉林省吉林市人，吉林化工学院讲师，博士，主要从事工程仿生学、工程图学及CAD教学与研究方面的工作。

收稿日期：2015-07-20

中图分类号：TP 24

文献标志码：B DOI：10.16039/j.cnki.cn22-1249.2015.11.012