考虑本身质量的圆柱螺旋弹簧动态特性研究

陆峰峰，杨国来

(南京理工大学 机械工程学院， 江苏 南京 210094)

考虑本身质量的圆柱螺旋弹簧动态特性研究

陆峰峰，杨国来

(南京理工大学 机械工程学院， 江苏 南京 210094)

摘要：从频域与时域两个角度，对考虑本身质量的一端固定、一端受迫振动的圆柱螺旋弹簧在理想稳定状态下及在实际非稳定状态下的振动情况进行理论分析，得到频域下的频率方程及时域下的各圈位移方程。建立可模拟弹簧动态性能的弹簧离散模型并进行仿真分析，对比仿真与理论分析结果，验证所推导的理论公式的正确性。

关键词：圆柱螺旋弹簧，频率方程，时域分析

Research on Spring Dynamic Characteristics with Consideration of Proper Inertia

LU Fengfeng, YANG Guolai

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

Abstract:The dynamics of a fixed-free end helical spring are analyzed both at the frequency-domain and the time-domain. Analytical expressions for coils’ displacements are obtained under two different spring state conditions: the ideal stable state and the realistic state. As a discrete spring model represents well springs’ dynamic behaviors in multi-body dynamics simulation, this model’s simulation results are used to examine the correctness of the analytical expressions.

Keywords:helical springs; natural frequencies; time-domain analysis

0引言

圆柱螺旋弹簧作为基本机械元件，经常作为减震或力输出元件被用于机械系统中。在使用大质量螺旋弹簧的场合，弹簧本身质量将引起弹簧内各圈振动不一致，呈现波动规律，导致动态大质量螺旋弹簧并不符合虎克定律。

工程中通常把弹簧本身质量的三分之一加入到与弹簧相连的系统中，以此来近似考虑弹簧本身质量对其动态性能的影响[1]。然而该种近似仅能在频域范围内表示弹簧振动特性，并不适用于时域内的动态情况[2]。

圆柱螺旋弹簧的研究主要集中于轴向压缩条件下频域范围内的固有特性研究，而在时域范围内弹簧动态性能的研究却很少。中南大学刘世清等把弹簧类比为一维弹性直杆来研究弹簧的固有频率特性[3]。同济大学虞爱民等推导了可计算“弯-扭-剪切”耦合的圆柱螺旋弹簧振型的显式解析公式[4]。华中工学院赵廷仕采用能量法与单元质点的牛顿运动定律推导了各种边界条件下的弹簧固有频率计算公式[5]。

现把弹簧类比为一维弹性杆，从频域与时域两个角度，研究一端固定、一端受迫振动弹簧在理想稳定状态下及在实际非稳定状态下的弹簧各圈振动特性。在AMESim多物理场仿真软件中建立离散弹簧模型，与理论分析结果进行对比来验证理论公式的正确性。

1弹簧固有频率与振动形式的理论计算

在不考虑阻尼的情况下，可把弹簧等效为一具有等效弹性模量E、密度ρ的等质量、等长度、等截面积的均匀一维纵向振动弹性杆[3]。

杆中各截面位移符合一维平面纵波波动方程[6]，其任一截面任一时刻的位移u(x,t)满足；

u(x,t)一般表达式为：

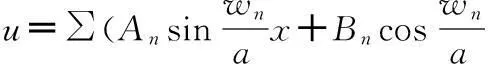
弹簧刚度k=42830N/m，有效圈质量M=4.278kg，长度(自由状态)l0=269.7mm，总圈数n=10，有效圈数nu=8.5。

假设弹簧一端固定、一端在外载作用下作受迫振动，有如下两种状态。

a) 理想稳定状态

当弹簧振动处于稳态时，u(x,t)为连续函数，式(1)的边界条件为：

从中解得弹簧固有角频率wn及位移u(x,t)：

(1)

(2)

式(1)与Becker在文献[7]中得到的固有频率方程相同。前三阶固有频率数值如表1。

表1　所测弹簧固有角频率　rad/s

弹簧自由端在外载荷作用下作简谐振动：

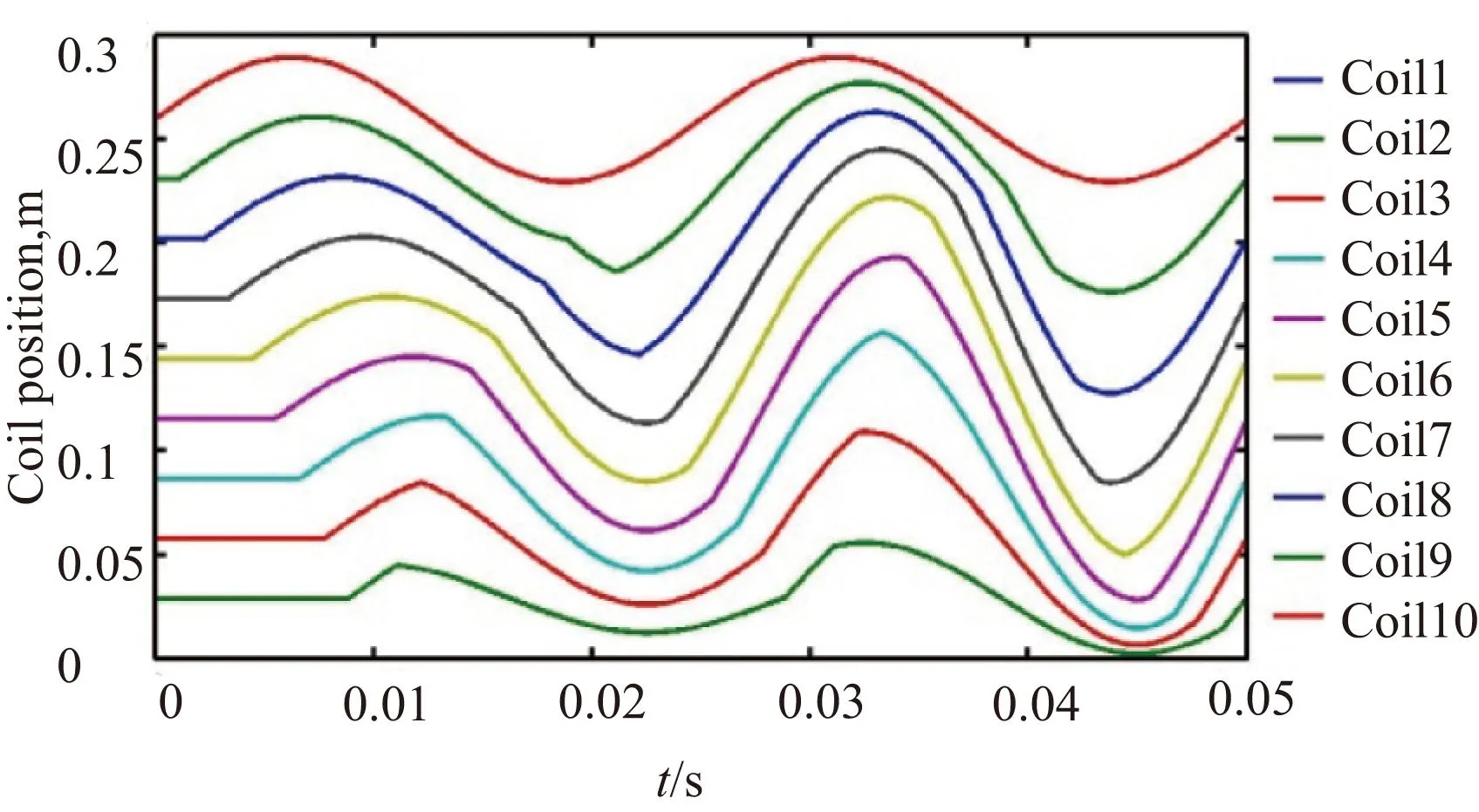
利用式(2)求得理想稳定状态下所测弹簧的振动形式，如图1。图1中从下到上10条曲线分别代表弹簧固定端到自由端各有效圈。

图1　理想稳定态弹簧各有效圈振动形式

b) 实际非稳定状态

在实际弹簧中，由于波的传递速度不可能无限大，从弹簧自由端振动开始，弹簧各圈之间必然有一个相位差。波在自由端于固定端间传递与反射，形成不同于理想稳定态的实际振动形式。

波在弹簧中的传递及反射过程如图2所示，横轴正向表示为弹簧固定端到自由端的长度方向。虚线代表弹簧振动波。

图2　波的传递过程

2)t0

3) (2i-1)t0≤t<2it0时，其中i≥2的整数，第一列波从弹簧固定端反射回自由端u(x,t)：

4) 2it0

当弹簧自由端的振动形式与稳定态时的相同，则实际弹簧的振动形式如图3。图3中从下到上10条曲线分别代表弹簧固定端到自由端各有效圈的振动形式。

图3　弹簧实际振动形式

2弹簧离散模型

根据文献[8]在多物理场仿真软件AMESim中建立无阻尼弹簧离散模型，如图4。利用该模型计算值可检验之前推导的理论公式。

图4　AMESim弹簧离散模型

2.1弹簧离散模型固有频率计算

单元数分别为9，17及136的离散弹簧模型前三阶固有角频率如表2。

表2　弹簧固有角频率理论值与仿真值　rad/s

当n=17时离散弹簧模型的固有角频率与理论计算值间的误差在3%之内。

2.2弹簧离散模型各有效圈振动形式

弹簧在非稳定状态下的振动形态理论值与单元数为17的离散模型的对比如图5。

图5　离散模型与理论振型比较(虚线：离散模型；实线：理论值)

从图5中可以发现，离散弹簧模型中各有效圈的振动幅值和相位与理论计算值十分相近。若提高离散模型的单元数，其仿真结果也就越趋近理论振动形态。弹簧离散模型与理论计算公式都很好地描述实际情况下波在弹簧的传递、反射及叠加过程。这也从侧面证明了文中推导的时域内弹簧动态公式的正确性。

3结语

把弹簧类比为一维弹性杆，在频域及时域内推导了弹簧的固有频率公式及弹簧各圈的振动位移公式。通过与弹簧离散模型的仿真值对比，验证了所推导公式的正确性。

从弹簧振动的时域分析可知，由于波传递速度的限制，弹簧各圈的振动必然具有相位差。弹簧内前进波与反射波相互叠加，形成了不同于弹簧稳定态的振动形式，直观地反映了弹簧各圈是否会出现碰撞现象。在时域内对弹簧的研究有助于更好地理解弹簧的振动特性，同时也是对可应用于多体动力学仿真的弹簧离散模型准确性的进一步验证。

参考文献:

[1] 罗蔚茵. 关于弹簧振子固有频率的进一步讨论 [J]. 大学物理, 1985,(4)(11): 9-11.

[2] 黄兆梁. 对有质量弹簧的振子系统振动周期的探讨 [J]. 大学物理, 2001,30(5): 32-34.

[3] 刘世清,邓国扬,何毅. 无负荷质量弹簧振动固有频率的研究[J]. 广西物理,1999,(04):10-12.

[4] YU A M, YANG C J.Formulationi and evaluation of an analytical study for cylindrical helical springs [J]. Acta Mechanica Solida Sinica,2010,(01):85-94.

[5] 赵廷仕. 圆柱螺旋弹簧的固有频率[J]. 机械强度,1980,(04):45-55.

[6] 赵凯华,罗蔚茵. 新概念物理教程. 力学 [M]. 北京: 高等教育出版社, 1995.

[7] Becker,L.E., Chassie,G.G. and Cleghorn,W.L., On the natural frequencies of helical compression springs[J]. International Journal of Mechanical Sciences, 2002, 44(1): 825-841.

[8] L. Guy, G. Bernard. Comportement dynamique des ressorts [J], Techniques de l'ingénieur Assemblages et fixations mécaniques, 1983,177(610):1-13.

[9] Lee,J. and Thompson,D.J., Dynamic stiffness formulation, free vibration and wave motion of helical springs[J]. Journal of Sound and Vibration, 2001, 239(1): 297-320.

[10] Lee,J., Free vibration analysis of cylindrical helical springs by the pseudospectral method[J]. Journal of Sound and Vibration, 2007, 302(1): 185-196.

[11] Haringx JA. On highly compressible helical springs and rubber rods, and their application for vibration-free mountings. Philips Research Reports 1949;4:49-80.

[12] Wittrick,W.H., On elastic wave propagation in helical springs.International Journal of Mechanical Sciences,1966, 8(1): 25-47.

[13] Pearson,D., The transfer matrix method forthe vibration of compressed helical springs.International Journal of Mechanical Engineering Sciences, 1982, 24(1): 163-171.

[14] Yildirim,V., Investigation of parameters affecting free vibration frequency of helical springs. International Journal for Numerical Methods in Engineering, 1996, 39(1): 99-114.

[15] Yildirim,V., Expression for predicting fundamental natural frequencies of non-cylindrical helical springs. Journal of Sound and Vibration, 2002, 252(1): 479-491.

[16] Yildirim,V., Free vibration analysis of non-cylindrical coil springs by combined used of the transfer matrix and the complementary functions method.Communications in Numerical Method in Engineering, 1997,13(1): 487-494.

收稿日期：2014-01-21

中图分类号：TH135+.1

文献标志码：A

文章编号：1671-5276(2015)04-0027-03

作者简介：陆峰峰(1988-)，男，江苏苏州人，硕士研究生，主要研究方向为机械设计。