一类广义弱压缩条件的同伦不动点存在性定理

马芙玲

(中山火炬职业技术学院公共课部，广东中山528436)



一类广义弱压缩条件的同伦不动点存在性定理

马芙玲

(中山火炬职业技术学院公共课部，广东中山528436)

[摘要]在偏序度量空间中引入了广义弱压缩映射条件，证明了同伦不动点的存在性定理，推广了原有的某些结果.

[关键词]偏序度量空间; 广义弱压缩条件; 不动点; 偏序集; 线性映射

1引言

度量空间不动点存在性问题已有比较完善的结果，这些结果在许多理论研究和实际应用中起到了重要作用. Matlhews(1994)[1]提出了偏序度量空间的概念，它是度量空间的推广，是一个不要求p(x，x)=0的广义度量空间，有着重要的意义.随着对该空间的深入研究及现实应用的需要， Ran和Reuring(2004)[2]对偏序度量空间不动点的存在性问题进行了卓有成效的研究，得到了一类广义弱压缩映射在拓扑同伦方面的不动点存在性定理.然而，他们的条件十分苛刻.基于偏序度量空间不动点的存在性问题有着重要的理论意义和实际应用价值，本文将尝试在更弱的条件下来讨论偏序度量空间不动点的存在性问题.

2预备知识

(i) p(x，x)=p(y，y)=p(x，y)当且仅当x=y；

(ii) p(x，x)≤p(x，y)；

(iii) p(x，y)=p(y，x)；

(iv) p(x，z)≤p(x，y)+p(y，z)-p(y，y).

序对(X，p)叫做偏度量空间，p叫做偏度量.在下文中，如无特殊说明，指的是(X，p).

注1Abbas和Nazir(2012)指出，若p(x，y)=0， 则由(i)和(ii)可推出x=y.

注2邻域Bp(x，ε)={y∈X;p(x，y)0可以生成一个拓扑τp.

注3如果(X，p)为一个偏度量空间，则会诱导一个度量

pS(x，y)=2p(x，y)-p(x，x)-p(y，y)，

故(X，pS)为一个度量空间.

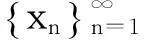
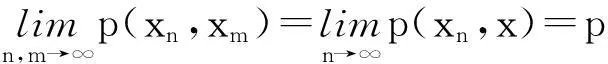
定义2.2[3]X是一个偏序度量空间：

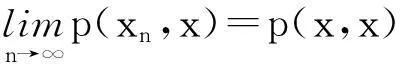
这样，偏度量p是完备的.

命题2.3[3]若X是偏序度量空间，因此

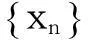
(X，p)是完备的当且仅当(X，pS)是完备的.

定义2.4[3]映射f:X→X叫做弱压缩映射，如果

p(fx，fy)≤p(x，y)-φ(p(x，y))， ∀x，y∈X.

最近，Abbas和Nazir(2004)[3]在偏序度量空间中获得了以下的弱压缩条件在同伦不动点存在性中的基本结果，即下文定理 2.5:

定理2.5(X，≤) 是一个存在完备偏度量p的偏序集，U是X的开子集，V是X的闭子集且U⊂V，设H:V×[0，1]→X且H(·，λ):V→X不减且连续，∀λ∈[0，1] ，如果以下条件满足：

(a) x≠H(x，λ)，∀x∈VU，λ∈[0，1]；

(b) ∀x，y∈V，H(y，λ)≤H(x，λ)，或H(x，λ)≤H(y，λ)，λ∈[0，1]；

(c) V中的元素是可比较的，且

∃φ∈Φ={φ:+→+;φ是递增且下半连续，φ(t)=0当且仅当t=0}，

s.t.p(H(x，λ)，H(y，λ))≤p(x，y)-φ(p(x，y))，λ∈[0，1]；

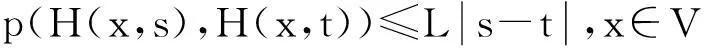
则H(，0)在U中有不动点当且仅当H(，1)在U中有不动点，这里有x0∈X且x0≤H(x0，λ)，λ∈[0，1].

定理2.5的条件过于苛刻，在实际应用中受到了限制.因此，本文如下定理3.1引入了一类广义的弱压缩映射条件，证明了拓扑同伦不动点存在性，推广了定理2.5，并得到了一些的推论.

3主要结果

定理3.1(X，≤)是一个存在完备偏度量p的偏序集，U是X的开子集，V是X的闭子集且U⊂V，设H:V×[0，1]→X且H(·，λ):V→X不减且连续，∀λ∈[0，1] ，如果以下条件满足：

(a1) x≠H(x，λ)，∀x∈VU，λ∈[0，1]；

(b1) ∀x，y∈V， H(y，λ)≤H(x，λ)，或H(x，λ)≤H(y，λ)，λ∈[0，1]；

(c1) V中的元素是可比较的，且

∃φ∈Φ={φ:+→+;φ是递增且下半连续，φ(t)=0当且仅当t=0}，

s.t.ψ(p(H(x，λ)，H(y，λ)))≤ψ(M(x，y))-φ(M(x，y))，

(1)

M(x，y)=a1p(x，y)+a2p(H(x，λ)，x)+a3p(H(y，λ)，y)+a4p(H(x，λ)，y)

(2)

且满足

a1+a2+a3+2a4<1；a1+2a2+a4<1，a1，a2>0，ai≥0(i=3，4)，λ∈[0，1]；

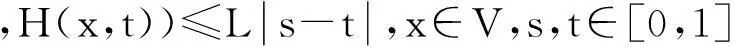
则若H(·，0)在U内存在不动点，那么H(·，λ)在U内也存在不动点，这里有x0∈X且x0≤H(x0，λ)，λ∈[0，1].

证记

A={λ∈[0，1];∃x∈U，x=H(x，λ)}，

若H(·，0)在U内存在不动点，则0∈A，故A≠∅，现将要证明A在[0，1]中既开又闭，则A=[0，1].

首先，证明A在[0，1]中是闭集，若λn→λ(n→∞)，λ∈[0，1]，因λn∈A，n=1，2，3，…，则

∃xn∈U，s.t.xn=H(xn，λn)，∀n，m∈N， xm∈U，

根据条件(b1)以及H(·，λ)的不减性，可知xm，xn是可比较的.而

p(xm，xn)=p(H(xm，λm)，H(xn，λn))

≤p(H(xm，λm)，H(xn，λm))+p(H(xn，λm)，H(xn，λn))-p(H(xn，λm)，H(xn，λm)).

(3)

因为ψ是线性递增的，故由(1)，(3)，(d1)得

ψ(p(xm，xn))=ψ(p(H(xm，λm)，H(xn，λn)))

≤ψ(p(H(xm，λm)，H(xn，λm)))+ψ(p(H(xn，λm)，H(xn，λn)))

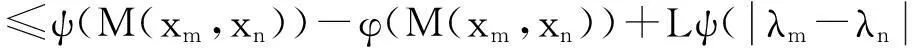
(4)

由(2)，(4)得

ψ(p(xm，xn))≤a1ψ(p(xm，xn))+a2ψ(p(H(xm，λm)，xm))+a3ψ(p(H(xn，λm)，xn))

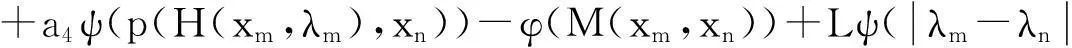
也即为

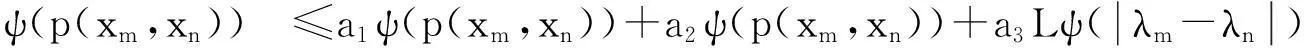
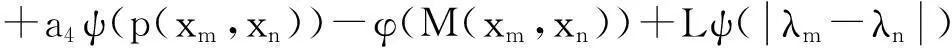
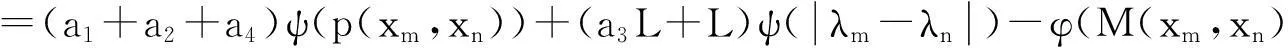
(5)

所以，由(5)式得

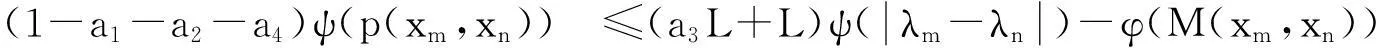
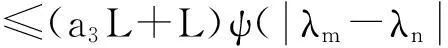
(6)

由条件(c1)，1-a1-a2-a4>0，当n，m→∞时，由(6)式知，有

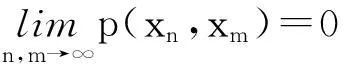
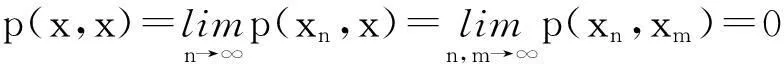
又因为xn∈U，x∈V，根据假设以及H(·，λ)不减性，x，xn是可比较的，

ψ(p(H(x，λ)，xn))=ψ(p(H(x，λ)，H(xn，λn))

≤ψ(p(H(x，λ)，H(xn，λ))+(p(H(xn，λ)，H(xn，λn))-p(H(xn，λ)，H(xn，λ)))

≤ψ(p(H(x，λ)，H(xn，λ)))+ψ(p(H(xn，λ)，H(xn，λn)))

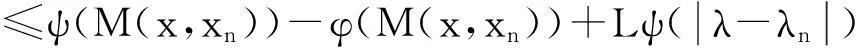
=a1ψ(p(x，xn))+a2ψ(p(H(x，λ)，x))+a3ψ(p(H(xn，λ)，xn))

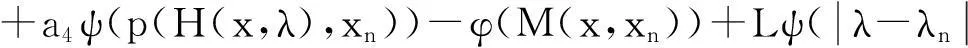
故由上述得

(1-a4)ψ(p(H(x，λ)，xn))

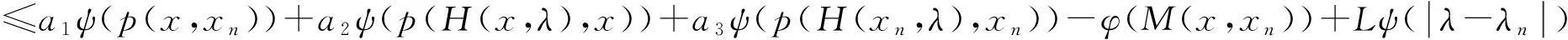
≤a1ψ(p(x，xn))+a2ψ[p(H(x，λ)，xn)+p(xn，x)-p(xn，xn)]

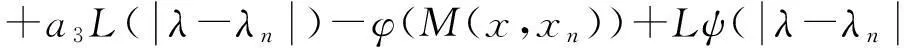
即

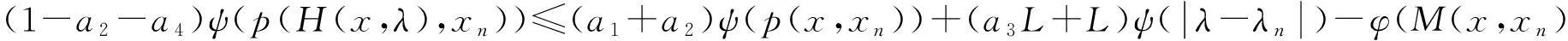
(7)

由(7)式得

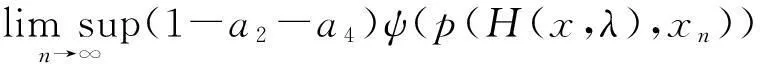
积极有效的思想政治教育不仅能够帮助学生养成良好的人生观、价值观和世界观，而且在解决学生在就业和择业期间所存在的一些思想和心理上的困惑方面也有着一定的指导价值。因此，笔者认为，高校教师特别是毕业班教师要特别注重加强对学生的思想政治教育工作，指导学生树立起崇高的人生理想和社会责任感，因为只有学生社会责任意识提升了，有了远大的人生理想，其在进行择业时才会更好地将个人的发展与国家和社会结合起来，深入到国家和社会最需要的行业去，不怕艰苦，努力奋斗，为国家的发展建功立业。[5]

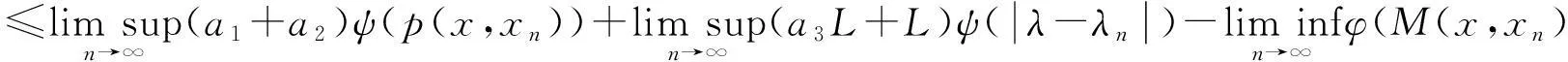
(8)

因此，由(8)式，可知

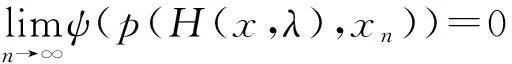
则

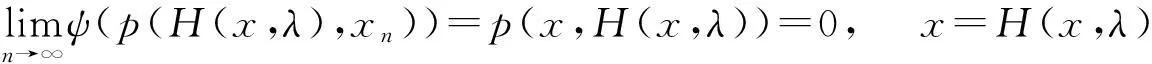
故λ∈A，及A为闭集，下证A为开集.

∀λ0∈A，∃x0∈U，s.t.x0=H(x0，λ0). 因为U为开集，∃r>0，s.tBp(x0，r)⊆U，固定ε>0，满足

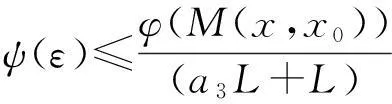
及

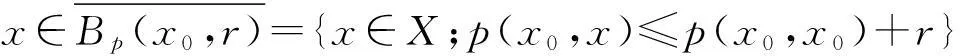
因为H(·，λ)是不减的，对于∀λ∈[0，1]，根据条件(b1)，知x，x0是可比较的，以及以下变形

ψ(p(H(x，λ)，x0))=ψ(p(H(x，λ)，H(x0，λ0))

≤ψ(p(H(x，λ)，H(x0，λ))+ψ(p(H(x0，λ)，H(x0，λ0))-ψ(p(H(x0，λ)，H(x0，λ))

≤ψ(p(H(x，λ)，H(x0，λ))+ψ(p(H(x0，λ)，H(x0，λ0))

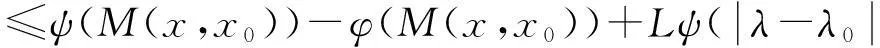
(9)

同理，根据已知条件和(9)式，可得到

ψ(p(H(x，λ)，x0))≤a1ψ(p(x，x0))+a2ψ(p(H(x，λ)，x))+a3ψ(p(H(x0，λ)，x0))

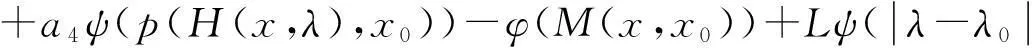
(10)

从而由(10)知

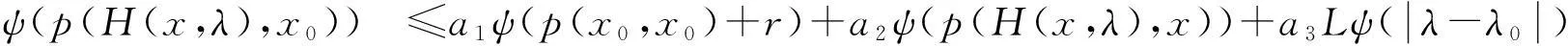
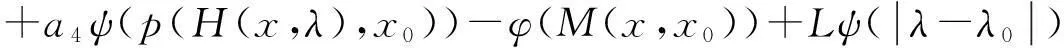
=a1ψ(p(x0，x0)+r)+a2ψ(p(H(x，λ)，x))+a4ψ(p(H(x，λ)，x0))

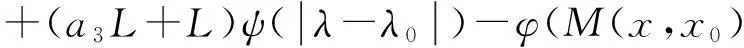
(11)

所以从(11)式得到

(1-a4)ψ(p(H(x，λ)，x0))

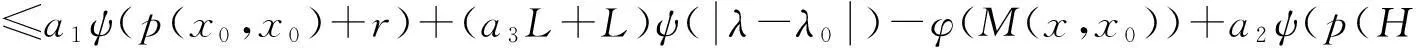
(12)

又因为

a2ψ(p(H(x，λ)，x))≤a2ψ(p(H(x，λ)，x0))+a2ψ(p(x0，x))-a2ψ(p(x0，x0))

≤a2ψ(p(H(x，λ)，x0))+a2ψ(p(x0，x0)+r).

所以由(12)及上式得

(1-a2-a4)ψ(p(H(x，λ)，x0))

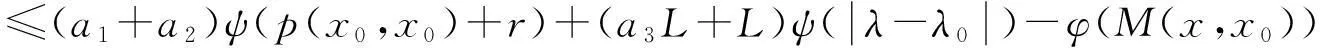
≤(a1+a2)ψ(p(x0，x0)+r)+(a3L+L)ψ(ε)-φ(M(x，x0)).

(13)

因为

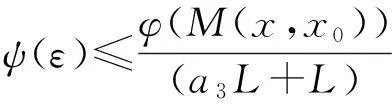
故根据(13)式，知

(1-a2-a4)ψ(p(H(x，λ)，x0))≤(a1+a2)ψ(p(x0，x0)+r).

即

ψ((1-a2-a4)p(H(x，λ)，x0))≤ψ((a1+a2)(p(x0，x0)+r)).

(14)

由于ψ的递增性，根据(14)式知

(1-a2-a4)p(H(x，λ)，x0)≤(a1+a2)(p(x0，x0)+r).

因为

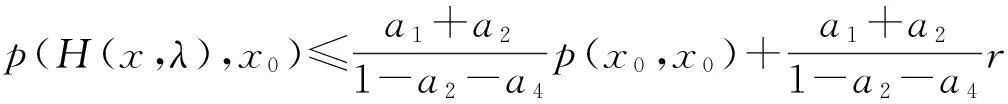
由于a1+2a2+a4<1，即

p(H(x，λ)，x0)≤p(x0，x0)+r，

如果在定理3.1中，令φ(t)=t，则得到如下推论：

推论3.2(X，≤)是一个存在完备偏度量p的偏序集，U是X的开子集，V是X的闭子集且U⊂V，设H:V×[0，1]→X且H(·，λ):V→X不减且连续，∀λ∈[0，1] ，如果以下条件满足：

(a2) x≠H(x，λ)，∀x∈VU，λ∈[0，1]；

(b2) ∀x，y∈V，H(y，λ)≤H(x，λ)，或H(x，λ)≤H(y，λ)，λ∈[0，1]；

(c2) V中的元素是可比较的，且

∃φ∈Φ={φ:+→+;φ是递增且下半连续，φ(t)=0当且仅当t=0}，

s.t.p(H(x，λ)，H(y，λ))≤M(x，y)-φ(M(x，y))，

ψ(ka+lb)=kψ(a)+lψ(b)，

M(x，y)=a1p(x，y)+a2p(H(x，λ)，x)+a3p(H(y，λ)，y)+a4p(H(x，λ)，y)

且满足

a1+a2+a3+2a4<1；a1+2a2+a4<1，a1，a2>0，ai≥0 (i=3，4)，λ∈[0，1].

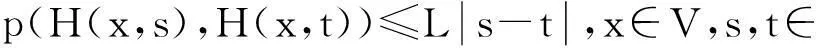
则若H(·，0)在U内存在不动点，那么H(·，λ)在U内也存在不动点，这里有x0∈X且x0≤H(x0，λ)，λ∈[0，1].

推论3.3(X，≤)是一个存在完备偏度量p的偏序集，U是X的开子集，V是X的闭子集且U⊂V，设H:V×[0，1]→X且H(·，λ):V→X不减且连续，∀λ∈[0，1] ，如果以下条件满足：

(a3) x≠H(x，λ)，∀x∈VU，λ∈[0，1]；

(b3) ∀x，y∈V，要么H(y，λ)≤H(x，λ)，要么H(x，λ)≤H(y，λ)，λ∈[0，1]；

(c3) V中的元素是可比较的，且

∃φ∈Φ={φ:+→+;φ是递增且下半连续，φ(t)=0当且仅当t=0}，

ψ(ka+lb)=kψ(a)+lψ(b)，

M(x，y)=a1p(x，y)+a2p(H(x，λ)，x)+a3p(H(y，λ)，y)+a4p(H(x，λ)，y)

且满足

a1+a2+a3+2a4<1；a1+2a2+a4<1，a1，a2>0，ai≥0 (i=3，4)，λ∈[0，1].

则若H(.，0)在U内存在不动点，那么H(·，λ)在U内也存在不动点，这里有x0∈X且x0≤H(x0，λ)，λ∈[0，1].

推论3.4(X，≤)是一个存在完备偏度量p的偏序集，U是X的开子集，V是X的闭子集且U⊂V，设H:V×[0，1]→X且H(·，λ):V→X不减且连续，∀λ∈[0，1]，如果以下条件满足：

(a4) x≠H(x，λ)，∀x∈VU，λ∈[0，1]；

(b4) ∀x，y∈V， H(y，λ)≤H(x，λ)，或H(x，λ)≤H(y，λ)，λ∈[0，1]；

(c4) V中的元素是可比较的，且

∃φ∈Φ={φ:+→+;φ是递增且下半连续，φ(t)=0当且仅当t=0}，

s.t.p(H(x，λ)，H(y，λ))≤αp(x，y)+β[p(H(x，λ)，x)+p(H(y，λ)，y)]+γp(H(x，λ)，y)

ψ(ka+lb)=kψ(a)+lψ(b)，

α+2β+2γ<1，α，β>0且γ≥0，λ∈[0，1]；

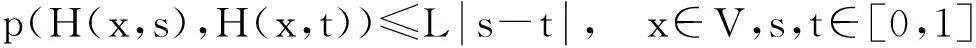
则若H(·，0)在U内存在不动点，那么H(·，λ)在U内也存在不动点，这里有x0∈X且x0≤H(x0，λ)，λ∈[0，1].

[参考文献]

[1]Matlhews S G. Partial metric topology[C]. Roc 8th Summer Conference on General Topology and Applocations，Ann New York Acard.Sci，1994，728:183-197.

[2]Ram ACM， Reuring，MC. A fixed point throrem in partially ordered sets and some applications to matrix equations[J].ProcAm.Math Soc， 2004， 132:1435-1443.

[3]Abbas M， Nazir T. Fixed point of generalized weakly contractive mappings in ordered partial metric spaces[J]. Springer-Verlag， 2012，1:1687-1812.

A Class of Generalized Weak Compression Conditions Existence

Theorem of Homotopy Fixed Point

MaFu-ling

(Department of Public Courses， Zhongshan Torch polytechnic， Zhongshan 528436， China)

Abstract:This paper introduces a generalized weak contraction mapping conditions in partial ordering metric space， proves the existence theorem of homotopy fixed point， and extends some of the original results.

Key words:partial order metric space; generalized weak compression conditions; fixed point; poset; linear mapping

[收稿日期]2015-01-13

[中图分类号]O189.1

[文献标识码]C

[文章编号]1672-1454(2015)02-0087-06