关于矩阵秩概念建立上的一种几何处理

郭聿琦，胡　洵，陈玉柱

(兰州大学数学与统计学院， 甘肃兰州730000)



关于矩阵秩概念建立上的一种几何处理

郭聿琦，胡洵，陈玉柱

(兰州大学数学与统计学院， 甘肃兰州730000)

[摘要]联系对偶线性空间和对偶线性映射等概念，给出了矩阵的行秩与列秩相等的一个几何证明.

[关键词]矩阵的行(列)秩； 对偶线性空间； 对偶基； 对偶线性映射

参考文献关于矩阵秩概念的建立，国内外众多文献分别给出了许多不同的处理方法，诸如，[1]～[7]，以及最近，郭聿琦等在参考文献[8]中给出的rspan(A)=rspan(A)的一个更自然，更直观的证明(这一处理已吸收到参考文献[9]中).

这里，我们再联系对偶线性空间和对偶线性映射等概念，给出下面定理2中关于rr(A)=rc(A)的一个新的几何证明(接下来，关于这个非负整数恰为rd(A)的证明，可以按照参考文献中的方法进行).

1矩阵秩概念建立上的宏观开发框架

矩阵秩概念的开发步骤为，首先给出

定义1[9]称数域F上矩阵

的列向量组{α1，α2，…，αn}的秩为A的列秩，称它的行向量组{α(1)，α(2)，…，α(m)}的秩为A的行秩.当A≠Om×n时，又称A的不为零的r阶子式的最大阶数为A的行列式秩，其中r阶子式指的是位于A的某r行某r列交叉处的r2个元素按原顺序形成的r阶子阵的行列式，r=1，2，…，min{m，n}；当A=Om×n时，定义A的行列式秩为0.因此，A的行秩，列秩和行列式秩都是非负整数，分别记它们为

rr(A)，rc(A) 和rd(A).

接着建立

定理2关于任意数域上的任意矩阵A，

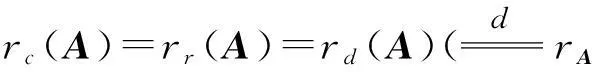
最后给出

定义3称定理2中的rA为A的秩.

2矩阵秩概念建立上的微观处理方法

矩阵秩概念建立上的微观处理方法体现在定理2的证明上.

第一类，证明rr(A)=rd(A)(定理2的第二个等式)，由行秩和列秩的对偶性，立得三非负整数相等的结论.

第二类，证明rr(A)=rc(A)(定理2的第一个等式)，再证明这一非负整数恰为rd(A).

具体的处理方法一般都是针对rr(A)=rd(A)和rr(A)=rc(A).[2]，[6]，[7]属于前者，我们收集到一种；[1]，[3]，[4]，[5]，[8]，[9]，[10] 属于后者，我们收集到的(包括我们建立的一种)共四种.

3为第二类补充一个几何的处理方法

定义4[11]令V为域F上一n维线性空间.V上所有线性函数组成的集合L(V，F)，在类似于线性变换的加法和数乘下构成域F上一n维线性空间，称它为V的对偶线性空间.记为

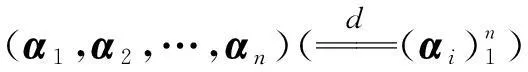
fi(αj)=δij，i，j=1，2，…，n

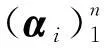
定理2的第一个等式的证明

首先罗列证明所需要的若干已知的事实如下.

事实1令V与V′分别为数域F上的n维和m维线性空间，(α1，α2，…，αn)和(β1，β2，…，βm)分别为V和V′的基底，L (V，V′)为V到V′的所有线性映射的集合.则

ζ∶fA

为L (V，V′)到Fm×n的一个双射，其中

f(α1，α2，…，αn)=(β1，β2，…，βm)A.

事实2[9](Sylvester 定理)令V与V′分别为数域F上的n维和m维线性空间，f为V到V′的线性映射.则

dim Kerf+dim Imf=dimV=n.

下面的事实是涉及线性映射的一个基本的线性相关性，它等价于Sylvester定理，见[9].

事实3[9]令V与V′分别为数域F上的n维和m维线性空间，f为V到V′的线性映射.令r=dim Kerf，(α1，α2，…，αr)为Kerf的一个基底，1≤r≤n-1，(即f不为零映射，也不为单射)，αr+1，αr+2，…，αl∈V.则α1，α2，…，αr，αr+1，…，αl线性相关当且仅当f(αr+1)，f(αr+2)，…，f(αl)线性相关.

证明还需要以下一些涉及对偶线性空间，对偶基底，以及对偶线性映射的已知事实.

事实4[11]令U，V分别为域F上的n维和m维线性空间，h为U到V的一个线性映射.则

(i) 关于任意g∈V*，有gh∈U*；

(ii) 定义V*到U*的一个映射h*为ggh，则h*为V*到U*的一个线性映射，称h*为h的对偶线性映射；

h∶U→V

事实5(事实4的推论)

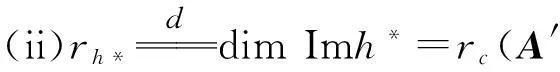
因此，有

(iii)rh=rh*⟺rc(A)=rc(A′)(=rr(A)).

于是，要证明rr(A)=rc(A)，根据事实1和5，只需证明

rh=rh*，

其中h和h*的意义见上面的事实4，下证rh=rh*.

令rh=r.则由事实2知，

dim Kerh=n-r.

又令(αr+1，αr+2，…，αn)为Kerh的一个基底，将其扩充为U的基底

(α1，…，αr，αr+1，…，αn).

由事实3知

(h(α1)=β1，h(α2)=β2， …，h(αr)=βr)

为Imh的基底，将其扩充为V的一个基底(β1，β2，…，βr，βr+1，…，βm).

因此

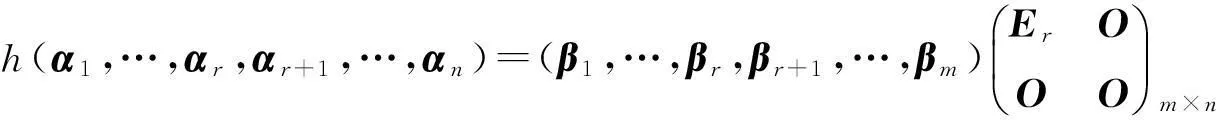
再根据事实4，

上两表示矩阵的列秩显然相同，从而rh=rh*.

后记

(i) 关于对偶线性映射理论的开发，一般地，是使用rr(A)=rc(A)，通过事实5得到rh=rh*.

(ii) 我们则通过(等价于Sylvester定理的)事实3，先建立rh=rh*，再通过事实5得到rr(A)=rc(A). 以此向读者进一步展示线性代数的代数理论与几何理论的内在联系，也展示了对偶线性空间和对偶线性映射在线性代数基础理论中的应用.

(iii) 但该文的目的绝不意味着，是在建议高校数学类各专业基础课程“高等代数”使用此方法去证明rr(A)=rc(A). 因为对偶线性映射的理论已超出“高等代数”课程大纲范围.纵然，“高等代数”课程要涉及对偶线性空间和对偶线性映射的内容，也是在后半本教材中，矩阵秩概念也实在用不着等到那时再建立.

[1]Karl W， Gruenberg， Alan J. Weir．Linear Geometry [M]．2nd Ed. New York： Springer-Verlag， Inc.， 1977.

[2]北京大学数学系几何与代数教研室代数小组.高等代数 [M].2版.北京：高等教育出版社，1988.

[3]北京大学数学系几何与代数教研室代数小组.高等代数 [M].3版.北京：高等教育出版社，2011.

[4]张贤科， 许甫华.高等代数学 [M].2版.北京：清华大学出版社，2004.

[5]Lee W，Johnson R，Dean Riess， Jimmy T. Arnold.Introduction to Linear Algebra [M]. 4nd Ed. New York： Addison Wesley Longman， Inc.，1999.

[6]郭聿琦， 岑嘉评， 徐贵桐. 线性代数导引 (面向21 世纪课程教材)[M]. 北京: 科学出版社，2004.

[7]Guo Yuqi，Karping Shum，Xu Guitong.Linear Algebra (Translated by P. K. Tam from the new version of [6])[M]. Beijing: Science Press，2007.

[8]郭聿琦， 王正攀， 梁星亮. 矩阵秩概念开发上的一个更简洁更干净的处理[J]. 高等理科教育， 2014， 4: 89-91.

[9]郭聿琦， 岑嘉评， 王正攀. 高等代数学教程[M]. 北京: 科学出版社， 2014.

[10]丘维声. 高等代数学习指导书 (上)[M]. 北京: 清华大学出版社， 2005.

[11]丘维声. 高等代数学习指导书 (下)[M]. 北京: 清华大学出版社， 2009.

A Geometrical Treatment in Constructions of

the Concept of Matrix Rank

GUOYu-qi，HUXun，CHENYu-zhu

(Department of Mathematics and Statistics， Lanzhou University， Lanzhou 730000， China)

Abstract:Contacting with the concepts of dual linear space and dual linear mapping， we have given a geometrical proof of the equality of row rank and column rank of a matrix.

Key words:row (column) rank of matrix; dual linear space; dual base; dual linear mapping

[基金项目]兰州大学教学研究项目资助

[收稿日期]2014-12-10

[中图分类号]O153

[文献标识码]C

[文章编号]1672-1454(2015)02-0072-04