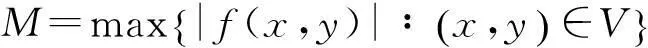关于解的延拓定理之注解

韩茂安，李继彬

(1.上海师范大学数学系,上海200234；　2.浙江师范大学数学系,金华321004)



关于解的延拓定理之注解

韩茂安1，李继彬2

(1.上海师范大学数学系,上海200234；2.浙江师范大学数学系,金华321004)

[摘要]在数学专业的常微分方程课程里有关解的存在唯一性、解的延拓和解对初值与参数的连续性构成了微分方程最基本的理论，这部分内容既是常微分方程的重点，又是该课程的难点.本文的目的是对解的延拓定理所涉及的概念和论证进行系统的梳理和完善，并希望能够弥补微分方程教材中的有关不足.

[关键词]延拓; 李卜希兹条件; 饱和解

1解的存在与唯一性定理

考虑标量微分方程

(1)

其中f为定义于下述矩形区域：

R∶|x-x0|≤a,|y-y0|≤b

(2)

上的连续函数(其中a与b为两个正数)，且存在常数L, 使对一切(x,y1),(x,y2)∈R成立

|f(x,y1)-f(x,y2)|≤L|y1-y2|.

如所周知，上述不等式称为李卜希兹条件. 熟知的Picard存在唯一性定理可叙述如下.

定理1在上述假设下微分方程(1)存在唯一的定义于区间[x0-h,x0+h]且满足初值条件y(x0)的解, 其中

上述定理是解的存在唯一性最经典的结果，在许多常微分方程教材中都有证明，见[1]-[16].

下面，我们讨论定义域更一般的标量方程. 首先给出区域的概念. 按照数学分析教材所定义的，如果一平面点集G可以写成一个非空连通开集和该开集的部分边界点的并，就说集合G是一个区域. 按照这个定义，区域可以开的(如果它是连通开集)，也可以是闭的(如果它是某一连通开集和该开集所有边界点的并) 也可以是非开非闭的. 例如，式(2)所定义的矩形R就是一个闭区域，而集合{(x,y)|x≥0,y>0}是一个区域，但它既不是开的，也不是闭的. 又如，集合{(x,y)|x≥0}∪{(x,y)|x≤0,y=0}就不是一个区域.

现在，我们可以叙述比定理1更为一般的存在唯一性定理了.

定理2设方程(1)中的函数f为定义于某平面区域G上的连续函数，且在G上关于y满足局部李卜希兹条件，即对G的任意内点(x0,y0), 都存在以该点为心且含于G的矩形区域，使得函数f在该区域上关于y满足李卜希兹条件，则微分方程(1)存在唯一的定义于以x0为心的某区间上且满足初值条件y(x0)=y0的解.

上述定理很容易利用定理1的结论推出.

上述两个定理都称为解的存在唯一性定理，并且都在许多常微分方程教材中出现，它们的共同点是解的存在区间都是局部的. 其实，在微分方程定性理论中起基石作用的解的存在唯一性定理不是上面的局部结果，而是解的大范围存在唯一性定理，这个定理是上面定理和解的延拓定理的直接推论. 下面一节我们就来详细讨论解的延拓定理.

2解的延拓定理

本段将假设方程(1)中的函数f为定义于某平面区域G上的连续函数，且在G上关于y满足局部李卜希兹条件. 首先，我们引入延拓与限制的概念.

定义1设φ(x) (x∈I)与φ1(x) (x∈I1)均为方程(1)的解，其中I1与I2为两个区间，如果

(i) I⊂I1, I≠I1;

(ii) ∀x∈I, φ(x)=φ1(x),

则称φ1为φ的延拓，同时称φ为φ1的限制.

这里注意，说定义在区间I上的函数φ为方程(1)的解，意味着函数φ在区间I上可导，且当x∈I时成立(x,φ(x))∈G.

易见，延拓具有传递性，即如果方程(1)有三个解φ, φ1与φ2, 且φ2为φ1的延拓，φ1为φ的延拓, 则φ2为φ的延拓.

有了延拓的概念，就自然出现下面三个问题：

问题1给定一个解，它什么时候存在延拓呢？

问题2一个解能够延拓到什么程度呢？换句话说，一个解是否存在最大范围的延拓解？

问题3这个最大范围的延拓解具有什么性质？

对于问题1与3，许多常微分方程教材中都有研究，后面将指出在这些研究中存在的不足，而对问题2，国内教材中则没有引起注意，而忽视了证明，本文的主要目的就是深入研究这一问题. 考虑到系统性和完整性，下面对这三个问题逐一详细研究，并得到比现有常微分方程教材中更为细致周密的结论. 关于第一个问题，有

命题1设y=φ(x)是方程(1) 的解，定义于区间I. 又设c是区间I的一个端点，则

(i) 若c∈I时，且点(c,φ(c))是G的内点，则该解必存在延拓；

(ii) 若c∉I时，且函数φ(x)在点c存在有限的单侧极限，记为d, 使得(c,d)∈G, 则该解必存在延拓.

那么，函数φ1就是φ的一个延拓. 这样的延拓称为φ的右向延拓. 类似地，可定义左向延拓.

如果c∉I，且函数φ(x)在点c有有限的单侧极限d，并使得(c,d)∈G, 那么导函数φ′(x)在点c也有有限的单侧极限，于是下列函数

就是φ的一个延拓. 证毕.

由命题1易见，如果G是一个开区域，且y=φ(x)的定义在一个闭区间上，那么这个解一定有延拓, 而且有很多个延拓. 这就是众多常微分方程教材中都讲到的结论. 但如果区域G是闭的，则方程(1) 定义于闭区间上的解未必存在延拓. 例如，线性方程

的非零解都定义在闭区间[0,1] 上，这样的解就不存在延拓. 又如，线性方程

在回答第二个问题之前，需要引入饱和解与饱和区间的概念.

定义2设φ为(1)定义于区间I上的一个解，如果这个解不存在延拓，则称它是(1)的饱和解(又称不可延拓解)，同时称区间I为饱和区间.

上述定义见[14] 等. 文献[12] 给出了饱和解定义的另一种说法，即

定义3设φ为(1)定义于区间I上的一个解，取x0∈I, 并令y0=φ(x0).如果方程(1)的过点(x0,y0)的任何其他解都是φ的限制，则称它是(1)的饱和解(又称不可延拓解)，同时称区间I为饱和区间.

上述两个定义有没有区别呢？下述命题给出了肯定的回答.

命题2设方程(1)有解y=φ(x), x∈I.如果这个解按照定义3是饱和解，则它按照定义2也是饱和解. 进一步，如果定义于区域G上的连续函数f在G上关于y满足局部李卜希兹条件，则定义2与定义3是等价的.

证命题的前半部分的结论是显然的，现证后半部分. 只需证，在对f所做的假设下，如果方程(1)有解

y=φ(x)，x∈I，φ(x0)=y0，

它按照定义2是饱和解，即它不存在延拓，那么它按照定义3也必是饱和解，即要证方程(1)的任一满足ψ(x0)=y0的解y=ψ(x),x∈J，都是φ的限制，除非它等于φ.先证在区间I∩J上成立φ=ψ.

我们指出, 如果不假设f在G上关于y满足局部李卜希兹条件, 则方程(1)可能有这样的解，它按照定义2是饱和解，而按照定义3它就不是饱和解.例如，方程

有过原点的解y=0与

按照定义2，这两个解都是饱和解，但按照定义3，它们都不是饱和解.

上述命题和例子说明定义2适用范围更大一些，而定义3只适用于解的存在唯一性处处成立的情形.

利用饱和解的概念，前面的第二个问题就是说，一个非饱和解能不能延拓成饱和解?下面的命题3给出了明确的答案.

命题3设方程(1)中的函数f在平面区域G上连续，且在G上关于y满足局部李卜希兹条件. 则该方程的任一非饱和解都能够延拓成唯一的饱和解.

证这里提供三种证明方法.

证法1现设y=φ(x),x∈I为方程(1)的一给定非饱和解，那么由命题2这个解就一定存在延拓，每个延拓都有一个定义区间. 我们把所有延拓的定义区间的左端集中在一起构成一点集E-，右端点集中在一起构成集合E+. 令

α=infE-,β=supE+,

证法2同前，设y=φ(x)，x∈I为方程(1)的一给定非饱和解, 其延拓ψ的定义区间记为Iψ, 令

证法3先设区域G是开集. 又设y=φ(x),x∈I为方程(1)的非饱和解, 则该解在区间的左端或右端可以延拓, 因此, 下列情况之一成立：

今以情况(a)为例证之. 因为G是开区域, 必存在无穷个严格递增的紧集的序列Kj⊂G，j≥1, 使得

令

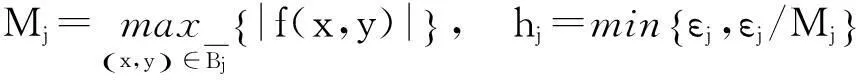
则由Picard存在唯一性定理的证明即知上述hj即合要求.

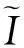
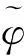
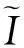
如果不要求方程(1) 中的函数f在G上关于y满足局部李卜希兹条件，则可证其任一非饱和解都能够延拓成饱和解. 详见[13]与[14].

在进一步讨论饱和解的性质之前，我们先引入下列定义.

定义4设(1)有定义于区间I的解y=φ(x)，I的端点为a与b, 其中-∞≤a

在上述定义中，当a=-∞时，“任意接近a的点x∈I”理解为“存在负数x∈I，且|x|可以任意大”，解y=φ(x)在端点a达到或逼近G的边界又可以说成这个解左端达到或逼近G的边界.

有了上述概念，我们就可以给出饱和解的性质如下.

命题4设方程(1)中的函数f在平面区域G上连续，且在G上关于y满足局部李卜希兹条件. 如果y=φ(x) (x∈I)是(1)的饱和解，则它在区间I的左右两端都能够达到或逼近区域G边界.

则

由微分中值定理知φ在(a,a+ε0]上是一致连续的, 从而

必存在有限, 且(a,φ(a+))∈V(因为V为紧集). 又因为V位于G内, 故点(a,φ(a+))为G的内点. 于是由命题1φ在x=a可进行左向延拓, 这与φ为饱和解矛盾. 证毕.

由命题3和命题4，即得下述解的延拓定理.

延拓定理设方程(1)中的函数f在平面区域G上连续，且在G上关于y满足局部李卜希兹条件. 则该方程的任一非饱和解都能够延拓成唯一的饱和解, 并且该饱和解在左右两端都达到或逼近区域G的边界.

通过对比可知，上述延拓定理的叙述不同于国内外所有现有教材，这里的叙述更加准确. 由这一延拓定理即得下述解的大范围存在唯一性定理.

大范围存在唯一性定理设方程(1)中的函数f在平面区域G上连续，且在G上关于y满足局部李卜希兹条件. 则该方程过G内任一点都存在唯一的饱和解.

最后指出，有关解的延拓的内容，国内许多教材[1-14]都存在下列一种或多种不足：

(i)没有明确给出饱和解的概念或延拓的概念不准确.

(ii)没有列出也没有证明命题3. 我们认为要完整证明解的延拓定理，证明命题3是必不可少的一步.

(iii)没有证明命题4, 只列出解的延拓定理，却述而不证.

(iv)在证明命题4 时，把区域G视为了开集，从而导致解的延拓定理的叙述不够完美或不够准确，其证明不够严密.

作者感谢Valery Romanovsky教授提供文献[16]，以及有益的讨论.

[参考文献]

[1]蔡燧林. 常微分方程[M]. 武汉：武汉大学出版社，2003.

[2]王高雄，周之铭，朱思铭. 常微分方程[M]. 3版. 北京：高等教育出版社，2006.

[3]阮炯. 常微分方程[M]. 上海：复旦大学出版社，1991.

[4]金福林，阮炯，黄振勋. 应用常微分方程[M]. 上海：复旦大学出版社，1991.

[5]楼红卫，林伟. 常微分方程[M]. 上海：复旦大学出版社，2007.

[6]丁同仁，李承治. 常微分方程教程[M].2版. 北京：北京大学出版社，2004.

[7]焦宝聪,王在洪, 时红廷. 常微分方程[M]. 北京：清华大学出版社，2008.

[8]张伟年,杜正东, 徐冰. 常微分方程[M]. 北京：高等教育出版社，2006.

[9]丁崇文. 常微分方程[M].2版. 厦门：厦门大学出版社，2006.

[10]王素云，李千路，等. 常微分方程[M]. 西安：西安电子科技大学出版社，2008.

[11]袁荣. 常微分方程[M]. 北京：高等教育出版社，2012.

[12]韩茂安，周盛凡，邢业朋，丁玮. 常微分方程[M]. 北京：高等教育出版社，2011.

[13]尤秉礼. 常微分方程补充教程[M]. 北京：人民教育出版社，1982.

[14]赵爱民，李美丽，韩茂安. 微分方程基本理论(重印版) [M]. 北京：科学出版社，2013.

[15]庞特里亚金. 常微分方程 [M]. 林武忠、倪明康译. 北京：高等教育出版社，2006.

[16]Bibikov, Yu N. 微分方程教程(俄文版)[M]. 彼得堡：列宁格勒大学出版社，1981.

[收稿日期]2014-10-23

[中图分类号]O175.1

[文献标识码]A

[文章编号]1672-1454(2015)02-0033-06