一类新的拟Bernstein-Bézier曲线

王青芳，陈晓彦，柏　凯，任　淼

(合肥工业大学数学学院， 安徽合肥230009)



一类新的拟Bernstein-Bézier曲线

王青芳，陈晓彦，柏凯，任淼

(合肥工业大学数学学院， 安徽合肥230009)

[摘要]构造了一类新的带双参数形状可调的拟Bernstein基函数，它是在三次Bernstein多项式的基础上扩展而成的一组n次拟Bernstein基.在此基础上，定义了带双形状参数的拟Bernstein-Bézier曲线，它保留了Bézier曲线的几何特征，并具有形状可调的特性.在控制点给定的情况下，可通过改变形状参数的值整体或局部地调控曲线的形状，同时给出参数控制及曲线拼接应用的实例.

[关键词]拟Bernstein基； 拟Bernstein-Bézier曲线； 形状参数； 几何造型

1引言

在计算机辅助几何设计中，由Bernstain多项式构造的Bézier曲线[1-2]简单且直观，具有举足轻重的意义.但一组控制顶点对应一条Bézier曲线，若要改变曲线的形状必须对控制顶点进行相应的调整，这使曲线构造较为死板和不便.为了使这一类曲线的调控更具灵活性，构造带形状参数的基函数或调配函数成为倍受欢迎的方法之一[3-4].文献[5]通过在多项式空间中构造一类带有n-1个局部控制参数的基函数对曲线进行局部控制，曲线的调控对应不同参数上的调控在实际应用中虽然更为细致，但也更为繁琐.文献[6]中利用递归方法提出一种新的基函数，基于这个递归定义了Bézier-like曲线，它的形状参数可以调整曲线的形状而并不改变控制点.Zhu Yuanpeng[7]等提出具有两个参数的αβ-Bernstein-like指数型的基函数，说明了指数型的形状参数对曲线预测式的调整有较好的优越性.而文献[8]则构造了带一个参数的三次三角Bézier曲线.刘植[9-10]等利用n次及n+1次Bernstein基的凸组合构造了一组新的n+1次多项式调配函数，使之具有类似Bernstein基的性质，同时引入多个形状参数作为对曲线形状的调控参数.

首先，本文定义的拟Bernstein基函数及拟Bernstein-Bézier曲线不但具有与Bernstein基函数及Bézier曲线类似的几何特性，而且当所有参数取1时即为n次Bernstein基函数及Bézier曲线.用该类基函数构造的含形状参数的拟Bernstein-Bézier曲线含有2个独立的形状参数，且与Bézier曲线次数一致，即次数并未增加.在不改变控制顶点位置的情况下，通过形状参数的取值变化，对曲线形状的调控比Bézier曲线更为灵活.其次，与现有其他扩展方法(如文献[5])相比，本文构造的拟Bernstein多项式构成了多项式空间的一组基函数，其相应的拟Bernstein-Bézier曲线用较少的形状参数对曲线进行整体与局部调控，既满足了不同曲线形状的设计控制需要，又避免了多个参数取值修改所造成的不必要的繁琐.最后，本文的数值实例说明该方法是切实有效的.

2拟Bernstein基函数

首先，在三次Bernstein基函数的基础上引入两个形状参数，并递归定义一组新的n次多项式如下.

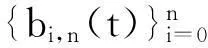
bi，n(t)=(1-t)bi，n-1(t)+tbi-1，n-1(t)，i=0，1，…，n，n>3

(1)

规定

b-1，n-1(t)=bn，n-1(t)=0，

其中

(2)

(i) 线性无关性；

(ii) 对称性：当λ=μ时，bi，n(t)=bn-i，n(1-t)；

(iii) 非负性：bi，n(t)≥0，i=0，1，…，n；

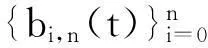
n=4时，

同理依次类推，由

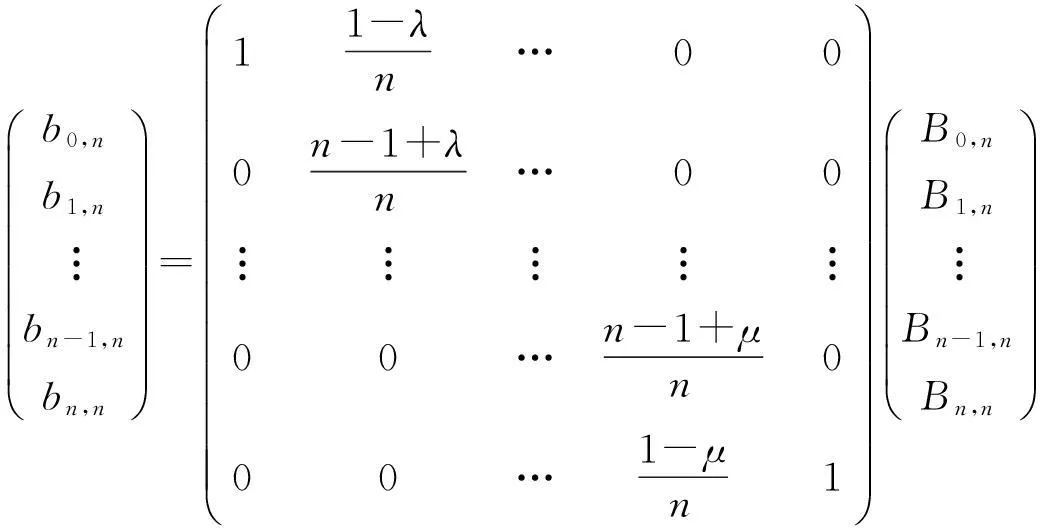
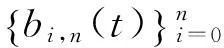
(ii)λ=μ时，容易验证

bi，3(t)=b3-i，3(1-t)，i=0，1，2，3

满足对称性，由(1)式容易看出，n次拟Bernstein多项式满足对称性.

bi，3≥0，i=0，1，2，3，

由(1)式立得非负性.

(iv) 容易验证

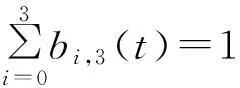
同时由递推公式可得

故

以此类推

(v) 由于

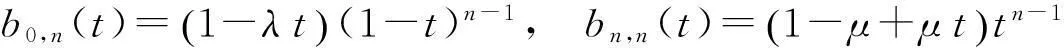
故

b0，n(0)=bn，n(1)=1.

下证

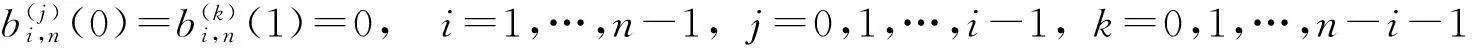
先验证当n=3和n=4时上述等式成立：

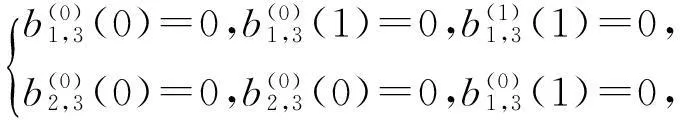
假设n=2k，n=2k-1时等式成立，若当n=2k+2，n=2k+1时也成立，即证.

当n=2k时成立，有

当n=2k-1时成立，有

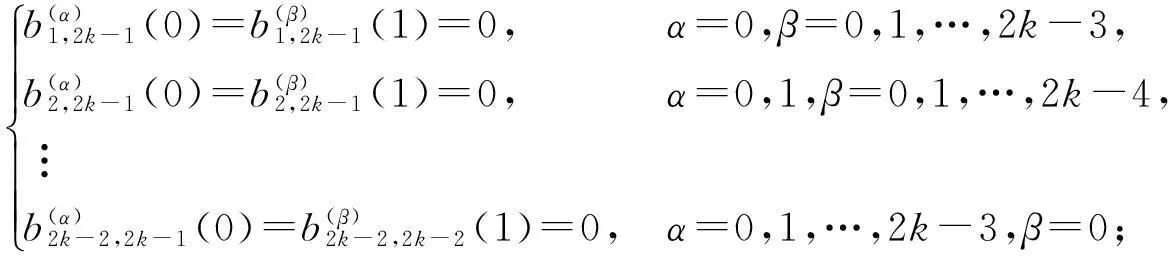
而当n=2k+1时，由递推公式

因为

bi，2k+1=(1-t)bi，2k+tbi-1，2k，

所以

依j=0，1，2，…展开恰好等式

当n=2k+1时成立.同理n=2k+2时也成立.由数学归纳法即证

其中i=1，…，n-1，j=0，1，…，i-1，k=0，1，…，n-i-1.

3拟Bernstein-Bézier曲线

(3)

显然，λ=μ=1时n次拟Bernstein-Bézier曲线p(t)退化为n次Bézier曲线.根据定理1，容易验证拟Bernstein-Bézier曲线具有如下性质.

定理2(3)式定义的带形状参数的拟Bernstein-Bézier曲线具有如下性质：

(i) 端点性质：

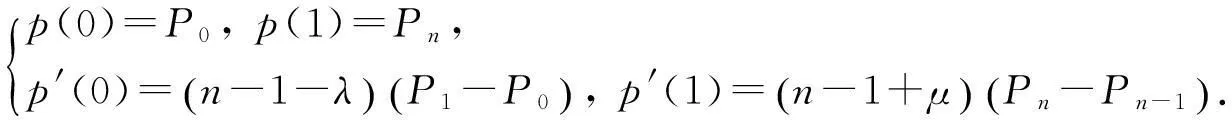
(ii) 对称性：由控制多边形P0P1…Pn-1Pn和PnPn-1…P1P0定义的两条拟Bernstein-Bézier曲线是相同的，只是定向相反.由拟Bernstein基函数的对称性立得

(iii) 凸包性：由拟Bernstein基函数的非负性和规范性性可得.

(iv) 几何不变性：由拟Bernstein基函数的规范性性易知，曲线不随坐标系的选取而改变，所以曲线p(t)具有几何不变性.

由定理2可看出，拟Bernstein-Bézier曲线与Bézier曲线有许多类似的性质，不同的是拟Bernstein-Bézier曲线中含有可调的形状参数，从(1)，(2)式显然可以看出，参数λ的值只对曲线(3)式的前半部分起作用，参数μ的值只对曲线的后半部分进行控制，即参数的取值可以整体或局部调控曲线的形状，这使曲线得在几何造型中更加灵活.

当n=3时，取λ=1，μ=-1，0，1，如图1所示；当n=4时，μ=-1，λ=-1，0，1，如图2所示.

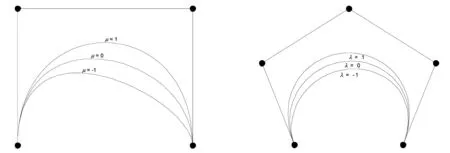
图1　形状参数μ对曲线形状的影响图2　形状参数λ对曲线形状的影响

给定控制点，当P0=Pn时，曲线是一条闭曲线.如图3，4所示的为4次拟Bernstein-Bézier曲线拟合的花瓣图案.图3仅以形状参数μ的调控为例，取

μ=-1.5，-1，-0.5，0，0.5，1，λ=1；

图4中仅以形状参数λ的调控为例，取

λ=-1.5，-1，-0.5，0，0.5，1，μ=1.

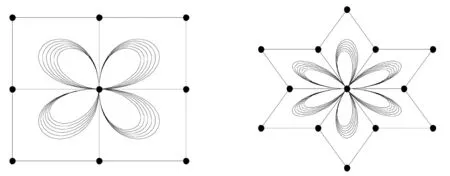
图3　形状参数μ调控的四片花瓣图案图4　形状参数λ调控的六芒星花瓣图案

4拟Bernstein-Bézier曲线的应用实例

在几何造型中，我们不仅可以对控制点进行调配，还可以对形状参数进行控制.当控制顶点给定时，可以利用形状参数更加理想的组合拟Bernstein-Bézier曲线形状.如图5，图6是模拟的童装口袋边缘及中央图案的组合曲线图形.口袋边缘是四段组合拟Bernstein-Bézier曲线，其中参数λ=μ=1.图5中的四叶草图案以及图6中的双心形图案的参数均取为λ=1，μ=0.5.

图5　四叶草图案的口袋造型图6　双心形图案的口袋造型　

除了用控制点对曲线进行控制，在控制点固定的情况下拟Bernstein-Bézier曲线也可通过对参数的调节生成不同的曲线.如图7中的六幅动物图案设计，均为相同的控制点.将曲线的主要部分分为曲线1、曲线2及曲线3三部分，其中曲线1部分均设参数值λ=μ=-1.曲线2部分即耳朵图案部分参数值设置，其中λ，μ值越小，耳朵越短小，λ，μ值越大，耳朵则偏细长，曲线3部分即动物脸图案部分参数值设置，λ，μ值越小，脸图案越偏椭圆，λ，μ值越大，脸图案则越呈“上瘦下胖”.

(1) λ2=1，μ2=1;λ3=1，μ3=1　　(2) λ2=0，μ2=0;λ3=0，μ3=0

(3) λ2=1，μ2=1;λ3=-1，μ3=-1　(4) λ2=1，μ2=-1;λ3=0，μ3=0

(5) λ2=-1，μ2=-1;λ3=-1，μ3=-1　(6) λ2=0，μ2=0;λ3=-1，μ3=-1图7　动物图案的参数控制(固定控制点)

5结论

本文给出了一类新的含有双参数的拟Bernstein多项式，它具有与传统Bernstein多项式类似的一些几何特性，如线性无关性，非负性，规范性等.与现有其他扩展方法相比，本文提出的拟Bernstein多项式构成了多项式空间的一组基函数.由于含有可调的形状参数，拟Bernstein基函数具有可调性.由拟Bernstein基函数构造的拟Bernstein-Bézier曲线也具备传统Bézier曲线的若干性质，且更加注重实际应用中曲线调控的方便和灵活性.在不改变控制顶点的前提下，可通过形状参数不同的取值对拟Bernstein-Bézier曲线局部或整体进行调控，从而达到多样化曲线设计的效果.数值实例表明本文方法是行之有效的.

[参考文献]

[1]施法中. 计算机辅助几何设计与非均匀有理B样条(修订版)[M]. 北京: 高等教育出版社， 2013：113-163.

[3]Zhu Yuan-peng， Han Xu-li. Quasi-Bernstein-Bézier polynomials over triangular domain with multiple shape parameters [J]. Applied Mathematics and Computation， 2015， 250: 181-192.

[4]Han Li-wen， Chu Ying， Qiu Zhi-yu. Generalized Bézier curves and surfaces based on Lupaq-analogue of Bernstein operator [J]. Journal of Computational and Applied Mathematics， 2014， 261: 352-363.

[5]Qin Xin-qiang， Qin Gang， Zhang Nian-juan， Shen Xiao-li， Yang Yang. A novel extension to the polynomial basis functions describing Bézier curves and surfaces of degree n with multiple shape parameters [J]. Applied Mathematics and Computation， 2013， 223: 1-16.

[6]Yan Lan-lan， Liang Jiong-feng. An extension of the Bézier model[J]. Applied Mathematics and Computation， 2011， 218: 2863-2879.

[7]Zhu Yuan-peng， Han Xu-li， Liu Sheng-jun. Curve construction based on fourαβ-Bernstein-like basis functions [J]. Journal of Computational and Applied Mathematics， 2015， 273: 160-181.

[8]Han Xi-an， Huang Xi-li， Ma Yi-chen. Shape analysis of cubic trigonometric Bézier curves with a shape parameter [J]. Applied Mathematics and Computation， 2010， 217(6): 2527-2533.

[9]刘植， 陈晓彦， 谢进， 时军. 一类形状可调的拟Bézier曲线[J]. 中国图象图形学报， 2009， 14(11): 2362-2368.

[10]刘植， 陈晓彦，江平. 带多形状参数的广义Bézier曲线曲面. 计算机辅助设计与图形学学报[J]. 2010， 22 (5): 838-844.

A Class of New Quasi-Bernstein-Bézier Curves

WANGQing-fang，CHENXiao-Yan，BAIKai，RENMiao

(School of Mathematics， Hefei University of Technology， Hefei 230009, China)

Abstract:A class of new Quasi-Bernstein basis functions with two shape parameters is constructed， which is the recursive approach of cubic Bernstein basis functions. Based on these basis functions， a new type of Quasi-Bernstein-Bézier curve with two shape parameters is defined. The new curve contains some properties of the classical Bernstein-Bézier curve. We present that the shape of the Quasi-Bernstein-Bézier curves can be adjusted globally or locally by changing the values of the shape parameters when the control polygon is maintained. Meanwhile， the examples illustrate that the altered shape parameters make it a valuable method for the design of curves.

Key words:Quasi-Bernstein basis function; Quasi-Bernstein-Bézier Curves; shape parameters; geometric modeling

[基金项目]国家自然科学基金(11471093); 高等学校博士学科点专项科研基金资助课题(20110111120026); 安徽省高等学校自然科学研究项目(KJ2014ZD30); 合肥工业大学大学生创新计划项目(2014CXCY558)

[收稿日期]2015-02-03；[修改日期]2015-03-10

[中图分类号]O241.5

[文献标识码]A

[文章编号]1672-1454(2015)02-0026-07