等周问题求解新探索

朱建华，赵　微，孟新柱

(山东科技大学数学与系统科学学院， 山东青岛266590)



等周问题求解新探索

朱建华，赵微，孟新柱

(山东科技大学数学与系统科学学院， 山东青岛266590)

[摘要]将实型Fourier级数延拓成复型Fourier级数，利用复型的Fourier级数和数学分析中的格林公式以及参数方程，借助Parseval等式，对等周问题进行求解.

[关键词]复型Fourier级数； 参数方程； 等周问题； Parseval等式

1引言

等周问题最早是由著名数学家Joham Beynoulli在1679年提出的， 即在具有定长的一切平面单纯闭曲线中， 圆是最大面积的曲线.在随后的300多年里，人们围绕等周问题开展了深入的研究与讨论， 并将其称为等周定理(等周不等式).现在比较典型的三种证明方法分别是1902年Hurwitz给出的第一个解析证明、1939年Schmidt的证明和1978年苏步青教授在文[1]中介绍的改良后的Hurwitz方法(即用Fourier级数的方法).近年来， 国内学者在等周问题的研究和拓广方面取得了一些新的进展，一般都是以Fourier级数为基础，对前人的方法进行改进[2-4].本文是在刘深泉[5]老师启示下，参考姚渊[6]等作者的方法，在他们的基础上，将实型Fourier级数延拓成复型Fourier级数，利用复型Fourier级数以及参数方程、格林公式以及几何知识对等周问题做进一步证明.

2主要内容

引理2(Parseval等式)如果f(x)，g(x)∈L2(T)，并且

则有

参考文献其具体的证明方法可以参照[7]中的证明.

首先利用参数方程，把平面曲线L的参数方程表示为

使其满足

L是光滑曲线，那么曲线的总长度为

因为L所形成的闭区域是单连通的，所以利用格林公式

取Q=x，P=-y.那么

为了计算方便，令s=1，现在以弧长作为参数

因为x(s)在0≤s≤1是按段光滑的，所以可以将其延拓成以1为周期的函数，即

其中an，bn为系数且满足

(1)

将Fourier级数延拓到复平面得

其中cn为复型Fourier级数的系数，仿照实型Fourier级数系数定义，其满足

(2)

比较(1)和(2)可以得出复型的Fourier级数系数满足

由x(s)是逐段光滑的，可得

由引理可以得到

由于x(s)在区间上面是光滑的，故x′(s)在[0，1]上是可积的，并且展开后的Fourier级数收敛于x′(s)，所以将其写成

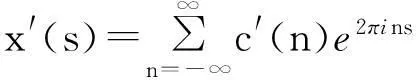
其中

(3)

由(2)，(3)两式可得

c′(n)=2πinc(n).

(4)

同理，还可以得到

其中

(5)

由(5)可得d′(n)=2πind(n). 由引理2可得

(6)

由(4)，(5)和(6)可得

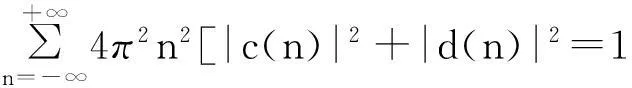
(7)

由引理2可得

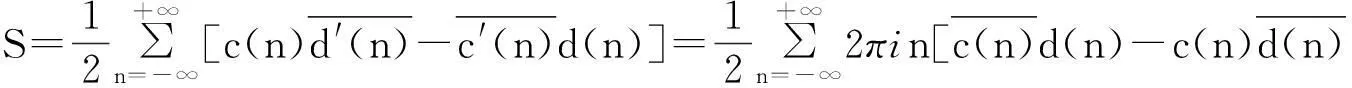
(8)

由(7)，(8)两式可以得出

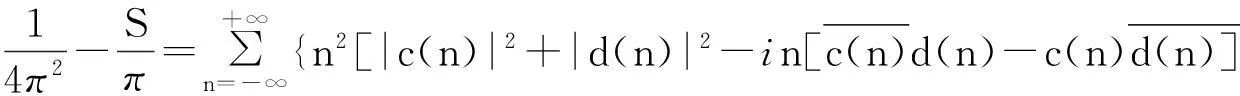
(9)

根据(4)，(5)两式，将(9)式化简可以得到

(10)

(11)

由(7)，(11)可以求得

(12)

将(12)拆开可得

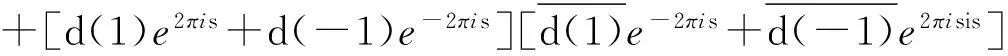
即

(13)

由(13)可得

(14)

由(13)，(14)可以得到

所以当封闭曲线的面积达到最大时恰好是一个圆.

3结语

定长封闭的曲线所围成的最大面积以及曲面面积一定的封闭曲面最大体积等问题，吸引着许多数学家的研究兴趣，也给出一些理论证明方法.本文的证明方法是将实型Fourier级数延拓成复型Fourier级数，利用它的性质，借助参数方程和格林公式，以及Parseval等式，在封闭的曲线所包围的面积达到最大时候，反推出它是一个圆.该方法也可以用来证明其它类似的问题.

[1]苏步青. 微分几何五讲[M]. 上海:上海科学技术出版社， 1978.

[2]汪遐昌. 均值不等式的重要应用-等周问题的一个简洁证明[J]. 四川师范大学学报(自然科学版) ， 1996， 19(6):81-82.

[3]姬小龙. 关于等周问题级数解法的一些改进[J].大学数学，2005，21(2): 82-84.

[4]项武义. 等周问题的一个初等证明[J]. 数学年刊A 辑(中文版) ， 2002， 23(1):7-12.

[5]刘深泉.美国数学月刊中的问题分析和教学中的应用[J].北京大学学报(哲学社会科学版)，2007，S(2)(5)：241-243.

[6]姚渊.关于等周问题级数解法的一些改进[J].青海师范大学学报(自然科学版)， 2006(3):15-17.

[7]河田龙夫著，周民强译.Fourier分析[M].北京：高等教育出版社，1984:108-112.

[8]华东师范大学数学系.数学分析[M].4版.北京：高等教育出版社，1990.

A New Exploration of Solving Isoperimetric Problem

ZHUJian-hua，ZHAOWei，MENGXin-zhu

(College of Mathematics and Systems Science， Shandong University of Science and Technology， Qingdao 266590，China)

Abstract:This paper extends real Fourier series into complex Fourier series， uses complex Fourier series， Green’s theorem in mathematical analysis， parametric equation and Parseval equality to solve isoperimetric problem.

Key words:complex Fourier series； parametric equation； isoperimetric problem； Parseval equality

[基金项目]国家自然科学基金(11371230)； 山东省自然科学基金(ZR2012AM012)； 山东科技大学教学研究“群星计划”基金(qx2013227)

[收稿日期]2014-11-12

[中图分类号]O174

[文献标识码]A

[文章编号]1672-1454(2015)02-0020-04