改进的随机PERT下寻找关键路径的新方法
黄永康,严 凌
(上海理工大学管理学院,上海200093)
改进的随机PERT下寻找关键路径的新方法
黄永康,严凌
(上海理工大学管理学院,上海200093)
[摘要]改进了随机PERT下寻找关键路径的方法.定义了随机路径时间变量的比较原则并据此确定概率关键路径;利用关于正态分布函数的不等式能对联合概率高精度估计的特性验证了概率关键指数较小时的概率关键路径的可信度;最后,实例阐明了随机关键路径方法.
[关键词]关键路径; 概率关键路径; PERT; 概率关键指数
1引言
PERT(计划评审技术)是利用网络分析制定计划以及对计划给以评价,它能够合理的安排人财物等资源,是现代项目管理的重要手段和技术[1].对于完成时间的不确定性或者随机性,早期学者们提出了用分布函数来研究活动完成时间并给出一些数学期望和方差的计算方法[2,3],这开启人们研究PERT的新思路.
概括起来有如下两种方式:其一,就是基于期望值和方差的方法把活动完成时间的随机性转化为确定性.自Beta分布假设以来众多研究对这种分布的性质在的网络分析上的应用性质有较多的深入的研究[4-6];但也有很多学者对这简单的便于理解应用的分布的假设提出质疑[7,8],是否有其他分布函数更实用.因此,在总结以往研究理论成果可以给予如下三个易见的概率分的概括:基于Beta分布下,完成时间由最可能、最乐观、最悲观三个时间可以确定;基于三角分布下,可由三点时间唯一确定;而在Gamma分布,其时间范围没有时间限制;这些分布都可以通过改变Beta分布函数的参数实现,同时,Beta分布函数的右偏性质与项目工程完成时间的实际吻合,因此多采用Beta分布将不确定的时间转化为单一确定的时间以确定关键路径.其二,计算完成时间准确的概率分布函数.Dolin和Sirvance(1990)在极端分布上做出了努力[9],Fatemi和Hashemin(1999)提出了转化方法简化多元重积分[10].但精确地分布函数因受到网络中活动的数目、活动的概率分布及活动间的相互关系等因素的影响,这些都涉及较为严格的数学计算这给应用带来很大不变.
本文在总结以往研究的基础上,旨在改进在随机性下寻找关键路径的方法,探索正态分布在关键路径的选择中的应用,同时利用三个不等式能够高精度的估算联合概率的特性验证在概率关键指数较小时选择概率关键路径的可信度.
2模型建立
2.1 模型假设
PERT下的工业项目大多数都是繁杂多步骤作业[11].在考虑到各个节点之间有众多作业,作业间的相互关联性,每个作业的完成时间的分布函数不可俱知的情况下,依据中心极限定理和正态分布的良好的性质,有如下假设:
(i) 活动完成时间长度服从正态分布;
(ii) 活动时间是相互独立的随机变量.
2.2 理论模型
在实数理论中有关序数的理论可知:对∀x,y∈,max{x,y}必为其中之一,不会出现第三个数字.然而,随机过程中,x,y都属于随机变量时,max{x,y}一般却不会是x,y二者中的任一个,通常是会出现第三个随机变量的.这一理论对于非确定性活动完成时间的研究是重要的,特别是在多维正态分布的前提下就更显得很有价值.故为得到一个活动完成时间的估计值,在随机不确定的活动时间集上我们重新定义序论.
假定活动完成时间集Ψ={α1,…,αk},以随机长度τ(αK)表示活动αk.

由多维正态分布的性质[12,13]可得:以(X,Y)表示二元正态随机向量,μ=(μ1,μ2)′表示其期望向量,其协方差矩阵为

在|r|<1时,随机变量Z=X-Y的期望值为μ1-μ2,那么

假定Φ(x)是标准正态分布的分布函数,可以得到如下等式:

(1)
μ1≥μ2.
(2)

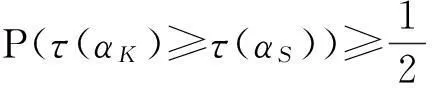
据定义2,可如下验证其满足序列的定义:

非对称性:若
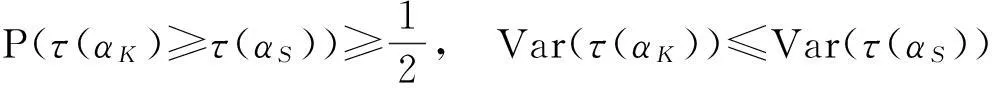
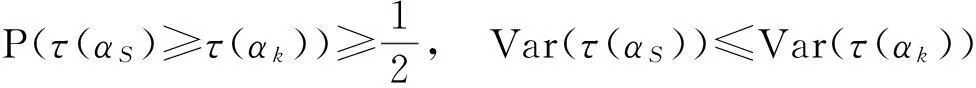
同时出现,也就是说αK,αS有相同的期望值和方差.因此,它们有同一个正态分布,故它们是非对称的.
传递性:根据式子(1),(2)是容易验证的.
因此,这样确定的一个随机性序列是满足自反性,非对称性及传递性的.故根据定义2确定的一个完成时间集{τ(αK),…,τ(αS)},规定以符号“”标明序列次序,如τ(αK)τ(αS).
2.3 模型验证
一般地,依据定义2可以方便的寻找到概率关键路径,但是当概率关键指数等于或者略微大于0.5下的情况,人们往往对所确定的概率关键路径是怀疑和不自信的.下面基于不等式给予证明,依据定义2寻找到的关键路径仍是自信的.
为证明不等式给出一个简化的积分公式[14]:

(3)
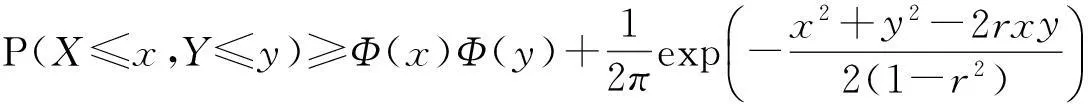
证令F(K)=Φ(x,y;kr),那么


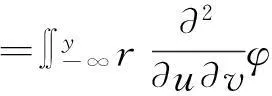
那么

(4)
以z=kr代入(4),得
当0 所以 同理可有如下不等式 实际上,Monhor(2010)通过数值运算证明了以上三个不等式对联合概率的真实值估计可得到一个高度和真实值相近的近似值[15],这将对下面条件概率是有用的. P(X≥μ1+ε|X≤Y)=1-P(X≤μ1+ε|X≤Y). (5) (6) 那么 (7) 因为 所以P(X≥μ1+ε|X≤Y)<0.5.故在确定概率关键路径Y下,错误的选择X的概率是远小于0.5的,这意味着犯错的概率是远小于选择正确的概率,故Y是概率关键路径.所以,定义2对寻找到概率关键路径是可以自信的. 3算例 节点集为{1,2,3,4,5},两点间路径时间的分布分别为 X12~N(6,4),X25~N(18,5),X23~N(9,9),X13~N(5,3), X24~N(19,27.4),X45~N(5,4),X34~N(9,9), 所以绘制如图1所示的它们的网络图. 图1 某网络计划图 根据假设可以得到如表1所示的所有路径及路径时间表. 表1 路径及其路径时间 由定义2,可以得到此路径序列为 X1≼X2≼X3≼X4. (8) 因此,路径1→2→4→5就是概率关键路径且P(x4≤30)=0.5.也就是说有50%的机会以30个单位时间完成计划.对于0.5的概率,这对于区间估计、假设检验等是小概率,但是因项目在实际运作中的不可重复性因此得到的数据和经验是很少的并且还有很多的随机性等等,这些原因决定在运营过程中很难有十足的把握也就是大的概率值,所以在项目管理中0.5的概率值仍然还有相当的应用价值. 如果把计划完成时间调整为31个单位时间,那么 P(X4≤31)=0.568. (9) 同理 P(X4≤32)=0.633, (10) P(X4≤33)=0.692. (11) 可以看到当完成时间调整为33的时候就有近0.7的概率确定这条概率路径,这一概率值足以让项目经理自信运营.同时,这也体现了模型的灵活性,项目经理在计划完成时间的选择上有一定的空间. 以上是根据定义2求得的概率关键路径,不过在概率关键指数较小的情形出现下,我们往往要进一步验证,所以可以依据式子(7)直接验证. 根据公式(1)和联合概率分布性质易得 P(X3≤X4)=0.560, (12) P(X2≤X3)=0.813. (13) 由定义2知,X2相比X3有接近1的概率不是关键路径,而X3相比X4据定义知不是关键路径,但概率关键指数也只有0.56的概率,因此,我们可以验证在概率关键指数较小时路径. 根据式子(7)可知,在X4是概率关键路径下错误选择X3概率是 P(X3≥30|X3≤X4)=1-P(X3≤30|X3≤X4)≤0.148. (14) 因此,在求得概率关键路径下错误的选择的概率X3仅有0.148,当然,项目经理对所选择的关键路径有足够的自信. 4结论 随机关键路径法是确定型关键路径方法的一个推广,它相比以往CPM严重依赖多个估计值,在寻找概率关键路径上有改进.此方法根据每个活动的分布特征值确定出关键路径,而且在项目完成时间选择上也有更大的灵活性.此外,由于正态分布函数的良好性质使得确定关键路径时使用到的联合概率分布函数的应用更为方便,验证关键路径也更加的方便.最后,不等式对联合概率的估计有着良好的精度这也利于应用其验证所选择的概率关键路径的可信度. [参考文献] [1]Maccrimmon K R, Ryavec C A. PERT假设的一个分析研究[J].运筹学,1964(12):6-17. [2]Malcolm D G, Roseboom J H, Clark C E, Fazar.网络评审计划应用[J].运筹学,1959,7(5):646-669. [3]Martin J.一个有向无环图的时间分布[J].运筹学,1965,13:46-66. [4]Sasieni M W.一个PERT时间的解释[J].管理科学,1986,32:1652-1653. [5]Littlefield T K, Randolph P H.有关PERT时间问题的回答[J].管理科学,1993,39:1086—91. [6]Gallagher C A.一个PERT假设的解释[J].管理科学,1987,33:1360. [7]Charles G A.一个PERT假设的的解释的回答[J].管理科学,1987,33(10). [8]Cheung T Y.最大网络流问题的八种方法的数值模拟比较[J].数学软件,1980,6(1):1-16. [9]Odin B, Sirvance M.随机网络和极值分布[J].计算机与运筹学,1990,17(4):397-409. [10]Fatemi G S M T, Hashemin SS.有关随机网络的一个新的分析算法和高斯积分方法[J].欧洲运筹学,1999,114:610-625. [11]曹光明,白思俊. 国外PERT/CPM网络计划技术发展的三个方面[J].系统工程理论与实践,1993,3. [12]茆诗松,程依鸣,濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社,2004. [13]Strom A, Peter B.经济学家的数学手册[M].上海:复旦大学出版社, 2001. [14]Plackett RL.多维正态分布降维公式[J].Biomerika,1954,41:351-360. [15]Monhor D.一个新的随机PERT下关键路径的概率方法[J].中欧运筹学,2011,19:615-633. An Improved New Method of Searching the Critical Path in Stochastic PERT HUANGYong-kang,YANLing (Business School, University of Shanghai for Science and Technology, Shanghai 200093, China) Abstract:This paper improves the method of searching the critical path in stochastic PERT. We defined the comparison principle of the time variable of random path and used the principle todetermine probabilistically critical path; we also used the inequality characteristics of the normal distribution function which can estimate the joint probability in high precision to verify the credibility in the case of having small probabilistic criticality index; finally, an illustrative example to search the critical path is presented. Key words:critical path; probabilistically critical path; PERT ; probabilistic criticality index [基金项目]上海市教委科研创新重点项目(12ZZ137) [收稿日期]2014-07-28 [中图分类号]TU 723.3 [文献标识码]B [文章编号]1672-1454(2015)02-0014-06


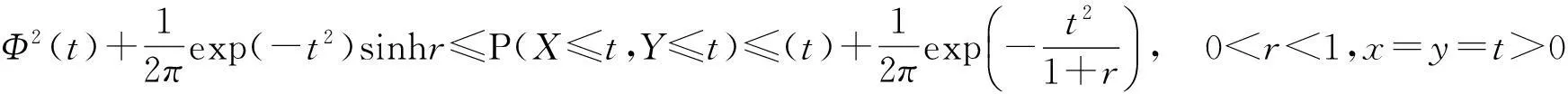

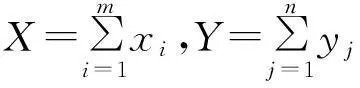



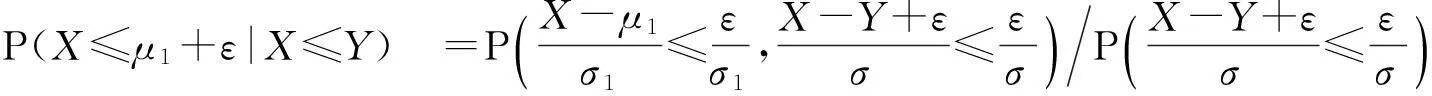

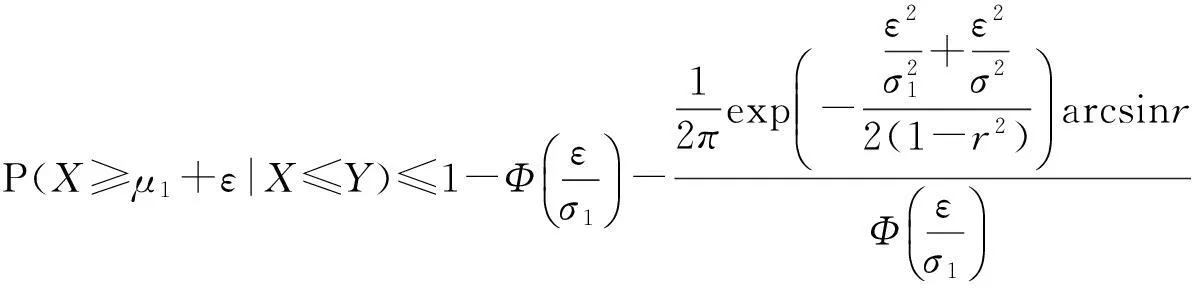


3.1 模型的应用求解

3.2 进一步讨论

