新课改下高一数学作业布置的优化策略

文远航 ，余盛利

(湖北师范学院 数学与统计学院，湖北 黄石　435002)

新课改下高一数学作业布置的优化策略

文远航 ，余盛利

(湖北师范学院 数学与统计学院，湖北 黄石435002)

摘要：现在高中数学作业的布置仍以传统的题海战术、“一刀切”等方式为主。为了使新课程的理念落到实处，作业改革必须引起高度的重视。高一数学作业布置的优化策略，可以从三个方面着手：从量走向质，从书本走向生活，从统一走向分层。

关键词：新课程；数学作业；布置优化

中图分类号：G633.6

文献标识码：A

文章编号：1009-2714(2015)04- 0115- 04

doi:10.3969/j.issn.1009-2714.2015.04.023

收稿日期：2015—09—18

作者简介：文远航(1988—)，女，湖北天门人，硕士研究生，主要研究方向为数学课程与教学论.

1高一数学作业布置的现状

作业是教学的延续，是教学活动中不可或缺的环节。在数学教学活动中，作业练习不仅可以使学生巩固课堂学到的知识、提高数学思维能力，还可以开阔他们的视野、培养他们的数学素养。此外作业也是教师教学效果的一种反馈形式，学生对作业的完成情况直接反映了教师的教学效果，教师可以根据它了解学生的学习情况，并以此为依据调整教学计划、改进教学方法，以此来提升课堂教学的质量。可是在数学学科上，尤其在高中阶段，“题海战术”扎根已久，数学作业不仅失去了它原本的教学意义，更让不少学子苦不堪言。究其原因，在于一线教师过度强调“知识的巩固”和“技能的强化”，双基的异化使得练习题繁难偏怪、学生完成数学作业只是低层度思维的机械式的重复，对练习题学生可能熟悉了，但未必生巧。[1]在很多高中学校，教师们片面追求学生解题能力的提升，大搞题海战术，追求熟能生巧，给学生布置大量的数学作业。而且大多数教师没有考虑到作业的有效性：不精挑细选，作业内容重复；不联系学生生活，习题过于形式化；不因材施教，简单采取“一刀切”的布置方式。这样布置的作业只会事倍功半，不仅加重学生的学习负担，禁锢学生的思想，抑制学生对数学学习的兴趣和积极性，甚至导致学生的厌学和排斥心理，无疑对学生的身心造成摧残，不利于学生的可持续发展。

2高一数学作业布置的优化

作为一名高中数学教师，要从根本上提高作业的质量，使学生看到数学的应用价值，并让具有不同基础、位于不同水平、持有不同爱好的每位同学通过完成作业都能得到应有的发展和实实在在的提高。

2.1　从“量”走向“质”

“注重提高学生的数学思维能力”是高中数学新课程的一大理念，数学作业作为课堂的延伸，在思维训练方面起着举足重轻的作用。教师应该首先明确做题不是目的，而是思维训练的手段。其次，工欲善其事必先利其器，教师不能简单随意地布置教科书或练习册上的题目，而是应该挑选能够凸显重难点、具有代表性和概括性、在巩固的基础上有拓展与提升的作业。最好能精选在知识点上可以以点带面、触类旁通的练习题，这样学生在完成习题时不仅能高效地完成练习任务，同时还训练了数学思维。总之，在素质教育的今天，应该尽量避免题海战术，追求高效能。[2]在“函数的应用”教学中，布置作业如下：

问题1：作出二次函数y=x2+4x-5 的图像，并写出一元二次方程x2+4x-5=0 的根.

问题2：若把y=x2+4x-5改为y=x2+4x-4，二次函数的图像以及一元二次方程的根会怎样变化？

问题3：若改为y=x2+4x+5呢？

问题4：通过对上面问题的进一步研究，请你概括出二次函数与一元二次方程更为一般的关系以及一元二次不等式解集的一般结论.

此时学生自己动手动脑，在题目的指引下从易到难，层层深入思考，开拓思维的同时巩固旧知识，并发现新知识。这样不仅可以条理清晰地得出所问，更是帮助学生学到了研究问题、分析问题的方法。若只布置问题1，各问题间在表面上看不到任何联系，则不会激发学生的进一步思考，学生做题只停留在就题论题的层面上。上例这样的作业更注重知识点之间的连贯性和变化性，学生在进行纵向思考的同时，自主地完成知识的整体建构，这样的效果当然要优于所谓的“题海战术”。

布置作业的一大目的在于培养学生思维的灵敏性、广阔性、深刻性和批判性。教师在布置作业时每一题的选择都要经过慎重的思考：该题目用到以前学过的哪些知识？这道题目是本节课哪个知识点的具体应用？该题能找到多少种解题方法？解该题容易发生哪些错误？[3]如果教师在布置作业前经过了这样的仔细思考，那所选出的作业才是具有启发性的、有利于学生自主建构知识网络的、高质量的作业，才能促进学生的高效学习，才能保证教学的有效进行。

2.2　从书本走向生活

“发展学生的数学应用意识”是新课程改革的一大基本理念。部分高中数学知识的学习是一种“历史知识”的学习，具有一定的被动性，这种被动性会使学生认识不到当前的学习与将来生活实践的联系，对数学的应用价值比较迷茫。弗赖登塔尔认为，数学来源于现实，存在于现实，并且应用于现实，数学教师的任务之一是帮助学生构造数学现实，并在此基础上发展他们的数学现实。[4]归到习题方面，就要求教师改变原来过于形式化的习题，取而代之的应该是更具现实背景的实质问题，主要是指从周围生活中可以找到原型、学生运用已掌握的数学知识可以分析解决的一类实际问题。这种作业在书本知识和学生的生活实际之间架起了一座桥梁，可以称之为实践型作业。对于实践型作业的布置，笔者认为教师应根据学生的特点，结合所学的内容，充分挖掘生活中的教学资源将实践性与书面性相结合。让学生运用所学的知识去解决现实生活中的问题，在真实的生活中实践体会数学，认识到数学的魅力。

1)在学习“等差数列”后，可以给学生布置与银行储蓄有关的实践型计算作业如下：

从高一开始以教育储蓄(整存整取)的方式，每月存200元，直到进入大学(即连续存3年)，到期(3年)时一次可支取本息多少元？比同档次的“零存整取”多收益多少元？

2)学习完“直线与圆的方程的应用”一节后，可布置如下习题：

①一座拱圆桥的水面跨度是20m，拱高4m.现有一船，宽10m，水面以上高3m，这条船能否从桥下通过?

②某台机器要安装三个齿轮，如图1所示，A与B啮合，C与B也啮合.若A轮的直径为200cm，B轮的直径为120cm，C轮的直径为250cm，且∠A=45° .试建立适当的坐标系，用坐标法求出A，C两齿轮的中心距离(精确到1cm).

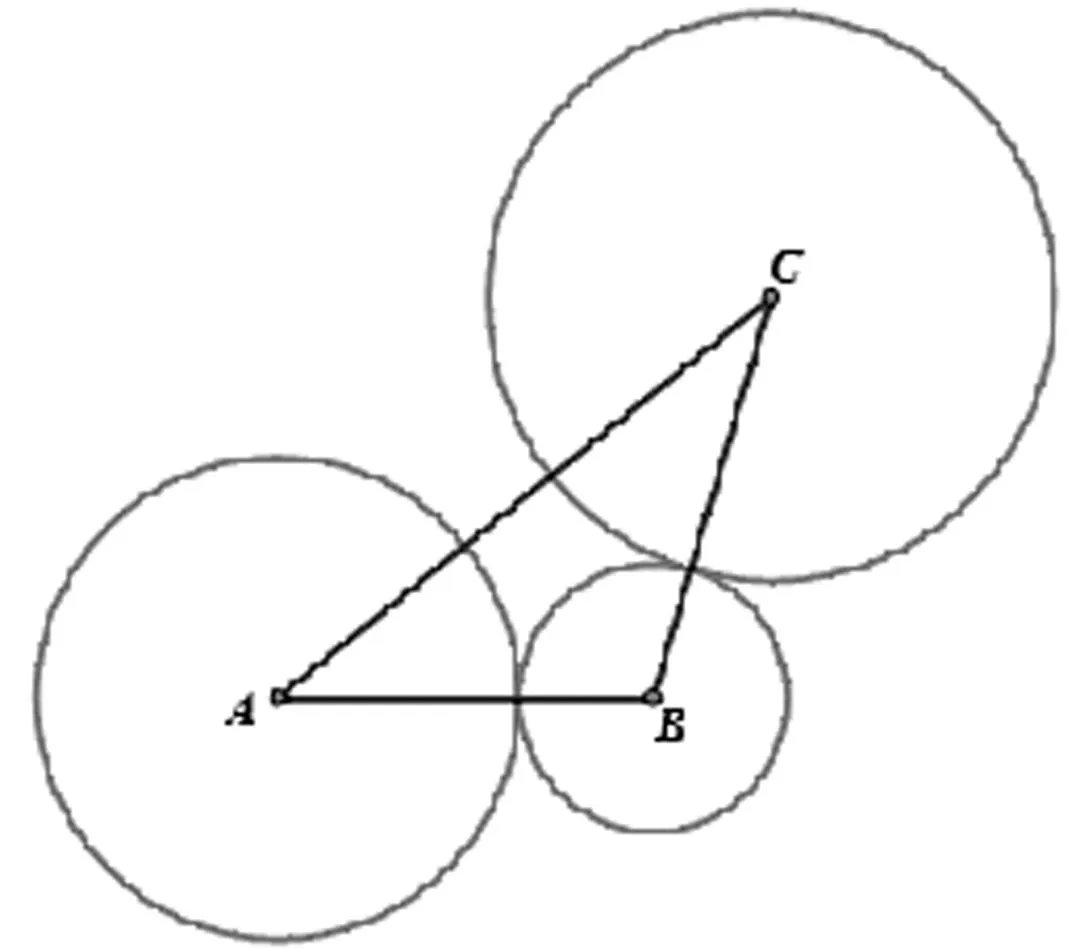
图1　三个齿轮啮合

这是与实际密切相关的问题。它使学生获得运用课堂里学到的数学知识、数学思想去解决生活实际问题的机会，能培养学生用数学眼光观察身边事物的习惯，提高学生的问题意识和数学素养。如所给出的两个例题，例1)中学生为了解决此题，就必须运用各种方法，通过各种途径了解有关银行的有关知识，如教育储蓄、整存整取、零存整取、定期储蓄与活期储蓄及利息和纳税的知识。例2)中的题联系现实，增强数学的存在感，使学生体会到数学在实际生活中的应用价值，在知识技能得到训练的同时，更是对学生情感、态度、价值观上潜移默化的影响。这样的作业往往比教师的讲解更深刻，学生需要经过自己的理解、调查、讨论来解决问题，在此过程中学生不仅能够增进对数学知识的理解与掌握水平，提高解题能力，还可以学到书本上没有的知识，深刻地体会到数学与社会生活的联系、数学的应用价值及学习数学的乐趣，形成良好的数学观和学习观，在调查探索过程中也能锻炼学生求真务实、刻苦钻研的心理品质。

3从统一走向分层

新课程十大基本理念中首倡“构建共同基础，提供发展平台”。共同基础包含两个层面的意思：一是为所有学生的基本要求，打好共同基础；二是为不同学生的不同数学要求，打好不同的基础。以往的数学作业布置中，学生认知发展水平的差异被忽视，全班无论多少学生，无论学生的学习水平如何参差不齐，所有学生的作业完全一致，这就导致了学优生“吃不饱”，而学困生“吃不了”，使得作业在很大程度上失去了其应有的教学意义。“提供多样课程，适应个性选择”也是新课程的一大理念。因材施教不应该仅仅用于课堂教学，作业的布置也应该照顾到不同学生的不同需求，布置不同层次的作业，适应个性选择。一般可分为三个层次：A 组主要夯实基础，B 组以侧重于能力的提升，C 组综合性强，属于探索拓展型。教师可以根据学生的实际情况，选出能够保证练习效果的A组习题，而B组、C组则供学生自主选择。

在学习完“直线的倾斜角与斜率”一节后，布置如下三个层次的作业供不同学生选择：

A 组：

1)已知四边形ABCD的四个顶点是A(2,3) ，B(1,-1) ，C(-1,-2) ，D(-2,-2) ，求四边形ABCD的四条边所在直线的斜率.

2)判断下列各对直线平行还是垂直：

①经过两点A(2,3) ，B(-1,0) 的直线l1，与经过点P(1,0) 且斜率为1 的直线l2；

②经过两点C(3,1) ，D(-2,0) 的直线l3，与经过点M(1,-4) 且斜率为-5 的直线l4.

B 组：

1)试确定m的值，使过点A(m,1)，B(-1,m)的直线与过点P(1,2)，Q(-5,0)的直线①平行；②垂直.

2)已知A(1,-1) ,B(2,2),C(3,0)三点，求点D坐标，使直线CD⊥AB，且CB∥AD.

C 组：

1)已知点M(2，2) 和N(5，-2) ，点P在x轴上， ∠MPN为直角，求点P的坐标.

2)已知四边形ABCD的四个顶点是A(m,n) ，B(6,1)，C(3,3)，D(2,5)，求m和n的值，使四边形ABCD为直角梯形.

3)经过点P(0,1) 作直线l，若直线l与连接A(1,2) ，B(2,1) 的线段总有公共点，找出直线l的倾斜角α与斜率k的取值范围，并说明理由.

布置作业时，教师将三组作业都呈现给学生，基本要求是完成B组作业，若认为B组有难度，至少应完成A组，有兴趣的同学可以完成C组，在讲解作业时，则三组作业都不遗漏。这样的作业对 A 层学生没有过大压力，可减轻学生课业负担，提高学生学习数学的兴趣和学好数学的信心，对学习较落后的学生有一定的激励作用。对学习较好的学生，不必重复训练，减轻学生负担，还给学生课余时间，避免厌学情绪的产生。对较优秀的学生也提供了训练，“吃不饱”的现象也会减少。这样分层帮助学生认识到自己的学习情况，有利于自我管理和调控，也体现了因材施教和发展性的教学原则，兼顾基础与难度，使每个学生都能在自己的最近发展区得到理想的发展，收获到学习带来的成就感、满足感和自信，对于学生形成受用终身的学习内驱力和成就动机。

4结语

教师是改革的践行者，在新课程改革理念的指导下，教师应该看到有效布置作业的重要性，不能使这个环节成为高中数学改革的“短板”。在布置作业时，教师要积极思考，善于疑问，敢于创新，勇于实践，以学生的全面持续发展为核心，努力探索，使数学作业真正成为提高教学质量的有力保障。

参考文献：

[1]何蕾.高中数学作业设计的理论和实践研究[D].江苏:苏州大学,2011．

[2]张月芳.创新数学作业布置提高教学实效[J]．宁夏教育,2010,(29):50~50．

[3]周小燕．优化数学作业布置的策略例谈[J]．新课程学习(下),2012,(7):27~27．

[4]张奠宙，宋乃庆．数学教育概论[M].北京:高等教育出版社,2012．

Optimization strategy for mathematics homework assignment

of Senior Grade guided by new curriculum reform

WEN Yuan-hang,YU Sheng-li

(College of Mathematics and Statistics, Hubei Normal University, Huangshi435002,China)

Abstract:The assignment of high school mathematics homework now is still based on the traditional ways such as endless exercises, sweeping approach and so on. In order to make the concept of the new curriculum to be implemented, the reform of homework must be paid more attention. The optimization strategy for mathematics homework assignment of Senior Grade1 can be consider from three aspects: from quantity to quality, from books to life, from uniform to hierarchical.

Key words:new curriculum; mathematics homework; optimization of assignment