数形结合巧利用 思维能力妙培养

戚卫东

摘 要：数形结合是一种重要的数学思想方法，小学数学教学中要利用数形结合培养学生的思维能力。

关键词：数形结合；小学数学；思维能力

钱学森教授曾指出：“教育工作的最终机制在于人脑的思维过程。”因此，进行思维训练，培养学生的思维能力，是小学数学教学的主要任务之一，是落实新课标理念、开发学生智能、提高学生素质的重要措施。数形结合是一种重要的数学思想方法，就是把抽象难懂的数学语言、数量关系与直观形象的几何图形、位置关系结合起来，通过抽象思维与形象思维的结合，可以使相对复杂的问题简单化，抽象问题具体化，从而起到发展思维能力的目的。那么，小学数学教学中如何利用数形结合培养学生的思维能力是值得探讨的问题之一。

一、利用数形结合，培养学生的形象思维能力

形象思维就是用直观形象和表象解决问题的思维。数形结合丰富了表象的储备，而表象的运动过程可促进形象思维发展。数学是以现实世界的数量关系和空间形式作为其研究的对象，而数和形是相互联系，也是可以相互转化的，我们在研究数的时候，往往要借助于形，在探讨形的性质时，又往往离不开数。因此，数形结合有助于培养学生对图形的想象能力，促进学生形象思维的发展。

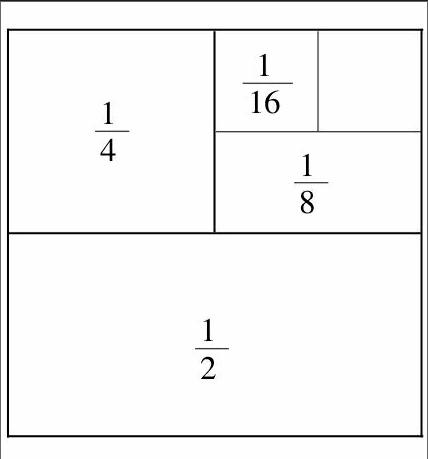
案例1：计算

这道题目，直接进行计算，需要进行通分，也可以得到结果。但如果我们联想到分数的计算可用几何直观图表示，那么现在可构造一个面积是1的正方形，如右图所示。先取它的一半作为，再取余下一半的一半作为，再取余下一半的一半作为，最后取余下一半的一半作为，余下部分的面积恰好也为，因而，不用计算，看图我们就可以得出：1

二、利用数形结合，培养学生的逻辑思维能力

儿童的认识规律一般来说是从直接感知到表象，再到形成科学概念的过程。表象介于感知和形成科学概念之间，教学中，抓住这个环节，就可以有效培养学生的逻辑思维能力，建立数学概念，并初步理解数学概念。

案例2：某位教师执教“乘法分配律”的教学片段如下：

1.情境导入，认知定律

同学们今天的表现都很积极主动，老师奖励给大家一些笑脸，你们知道这上面一共有多少个笑脸吗？

出示笑脸图，每行有六个白色笑脸图、四个灰色笑脸图，共五行。（渗透数形结合思想，以图想数，数形结合，引发学生思考）

学生充分讨论后汇报两种解法：

①先算出1行有多少个笑脸，再算出5行共有多少个笑脸。

列式为：（6+4）×5=50（个）

②先算出白色笑脸、灰色笑脸各有多少个，再算出一共有多少个笑脸。

列式为：6×5+4×5=50（个）

师：因为结果相同，我们就可以用等号连接。

板书：（6+4）×5=6×5+4×5或6×5+4×5=（6+4）×5

引导学生观察，使学生看到两种解法算式虽然不同，但结果都是50个，使学生明确两个算式相等。同时引导学生从不同的角度思考问题的思维方式，增强学生的逻辑思维能力。

分别观察有什么特点？（数字一样，符号一样）（6+4）×5是6和4的和乘5，而6×5+4×5是6和4都和5相乘，再把积相加，5我们可以叫同一个因数，或相同因数。

（6+4）×5=6×5+4×5这个算式中左边的式子是怎样等于右边的呢？

老师画线演示如下：

是不是有这样特点的题都相等呢？（激发学生举例验证）

2.验证猜测，概括定律

启发提问：

（1）师：观察这两个等式的特点，你们能再写一个符合上面特点的等式吗？

（学生举例，教师板书在上式的下面。请学生举2～3个例子，能口算的口算验证，不能口算计算验证。强调：不要只举因数是一位数的例子）

①抽象本质特征。

师：观察这几组算式，等号左边的算式有什么相同点？等号右边的算式有什么相同点？左右两边算式有什么关系？

学生先独自思考再小组讨论，汇报结果。

②归纳定律。

师：看来同学们已经发现了我们数学中的秘密，请你们把发现的秘密小声地说给旁边的同学听听。

（2）请学生汇报结果，概括出乘法分配律。（不要求学生必须按照书中叙述，只要意思接近即可）

教师板书：两个数的和与一个数相乘，可以先把它们分别与这个数相乘，再相加。这叫做乘法分配律。

（3）为了简便，如果用a，b，c表示3个数，乘法分配律用字母怎样表示？

板书：（a+b）×c=a×c+b×c

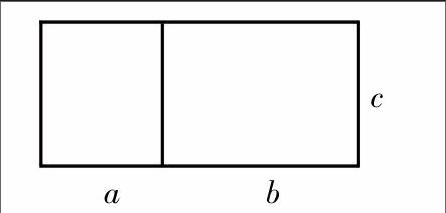
（4）启发学生思考，乘法分配律：（a+b）×c=a×c+b×c能不能用图形进行表示呢？

（渗透数形结合思想，体现以数想形，数形结合，初步理解定律）

从图可以看出：大长方形的面积等于两个小长方形面积之和。

即：（a+b）×c=a×c+b×c

总之，数形结合是一种重要的数学思想，在小学数学教学中，数形结合能为学生提供合适的形象材料，可以将抽象的问题具体化，增强学生思维能力，提高学生数学应用意识和综合素质。

参考文献：

林华珍.渗透数形结合教学 培养思维的灵活性[J].才智，2012（24）.

编辑 赵飞飞