现有铁路桥疲劳可靠性的评价

张　薇

(黑龙江省水利水电勘测设计研究院，哈尔滨 150080)



现有铁路桥疲劳可靠性的评价

张薇

(黑龙江省水利水电勘测设计研究院，哈尔滨 150080)

摘要：通过检测桥梁的重要构件，程序系统可对现有铁路桥的疲劳可靠性和剩余疲劳寿命进行评价。关键部位的构件从感受最大应力幅度的那些材料中被选择出来，比对应的忍耐力在二百万个周期还要高。一个改善构件疲劳强度的方法正在被实施。对应的疲劳试验正被实施，为了核实合格的构件种类，对于这特殊细节和已修复的构件。通过现在推荐的程序，比较各种不同的图解结果也正在被获得到。以下被发现：简单确定性的程序可以适应十分相符合的信息在可接受准确性的剩余疲劳寿命的桥上。

关键词：可靠性水平；剩余疲劳寿命；乘客流量；重合率；改进方法；疲劳测试

1概述

一些倒塌的桥是由于疲劳裂缝引起的，当此疲劳裂缝增大到一定程度时，将引起钢桥的构件破坏，这引起了有关评价钢桥剩余疲劳寿命人员的广泛兴趣。评估钢桥疲劳损坏的技术正在被许多研究人员探索。不同于公路桥应用的活荷载在铁路桥可被明确地描述，活荷与恒荷的比值是很高的。同时，服务负荷效果通常选择于接近设计强度，这可能引起严重疲劳负荷情况。

确定性程序被广泛地运用于评估结构疲劳损坏的情况，但是概率性程序是以可靠性理论为基础，最近也被更多运用到更合理的评价疲劳损害中。使用现有结构疲劳理论，以可靠性评价概率性基础为背景的疲劳破坏和发展的可靠性基础依据，为抵抗疲劳的设计方案[1]。在20世纪80代早期，断裂力学研究方法正在被应用在疲劳裂缝的增长上。各种不同确定性程序和概率性程序也已经被提议为S-N曲线分析。这次研究的桥有3跨3个单元，平行弦桁架主跨跨度为90-90-90m，板梁桥的引道布置在桥的两边。桥纵断面见图1。

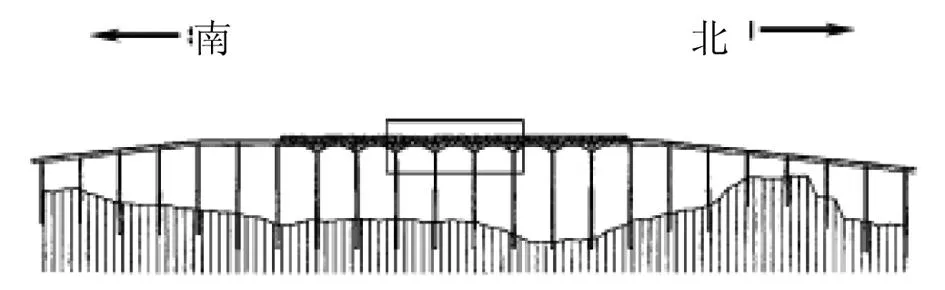
a)全貌图

b)主跨图

因为考虑过桥在它的15a服务期过后，在桥面构造上被发现有疲劳裂缝，它的安全性关联着城市的治理。因此，对全部结构进行安检和以疲劳寿命为主要构件的桁架和板梁的跨度正在被评估。应当严格检查桥梁构件，特殊是一些连接了横撑的上弦构件，有特殊细节的节点板不合格可能是制造业引起的。因此这样的构件不能被使用，应当用对应的疲劳试验核实后再用适当的种类。即使附加一些修复的细节也要经过疲劳试验。

2预测疲劳寿命

疲劳寿命的预测方式以S-N曲线为基础，主动绘制疲劳裂缝的平面图，如N是应力范围的一个函数△σi， S-N曲线通常被理想化，如线状或双线性函数。线状关系能用下面的方程式表示如下：

△σm·N=C

(1)

式中：C为一个给定材料和疲劳状态的常数；指数M为一个物质的参数，其范围2~4。

疲劳荷载通常包含可变振幅应力循环。因此，线状的累积疲劳palmgren-miner的损坏规则广泛地被应用到评估累积疲劳损坏中：

(2)

式中：ni为△σi应力范围中的周期数字；Ni为在重复恒定应力△σi作用下的疲劳寿命，其强调的范围在结构组成部分△σi中。在这个关系中，疲劳损坏被假定为线状累积和疲劳损坏，由于每个应力范围是成比例的，对于特殊的应力幅度来说。

其中K(k=1，2，3，…，K)列车的类型是在桥上进行交通服务，跨越桥的kth列车的数目一年的数目为nk1个，其中疲劳寿命Yr初步可用下面的计算式为：

(3)

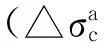
3荷载模型

估测疲劳寿命是基于所获得的应力作用范围及应力作用时间下，通过感应那些运行的地铁所获得。对于正确评价疲劳可靠性，适当的活荷载模型是必须的。在这一部分，所用的程序决定所承担的活荷载是能被显示的。一列列车包括10个车厢，列车车厢的侧面图见图2。地铁车厢的布置见表1，空车厢与装满旅客的车厢的行车重量见表2。

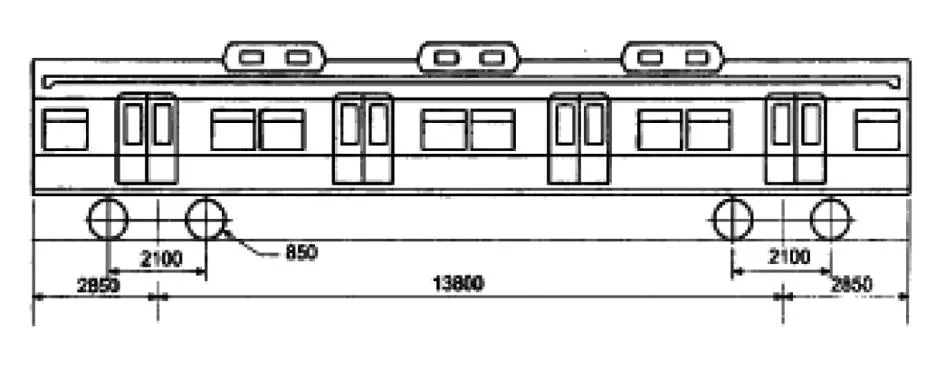
图2　车厢的侧面图

车厢号车厢安排10T0-M1-M2-M1-M2-T-T-M1-M2-T0

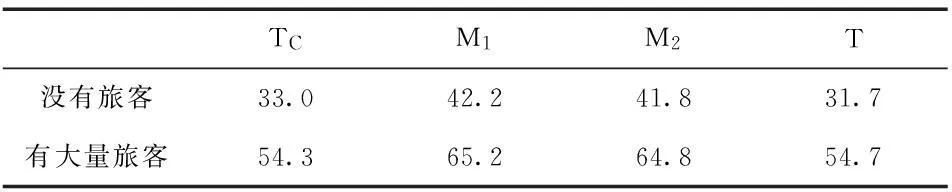
表2　行车的重量　t

在分析桥梁的状态时，有很多不确定的要素，但是在这一项研究中，仅仅不确定的乘客流量也被考虑进去。然而，结构要素的应力反应一方面被适当的假定为在荷载测试结果区域下被标定为恰当的。乘客运量被定义为乘客的数量与规定的乘客容量的比值。一般划定为160人。一个旅客的平均重量假定为60 kg，最大的旅客运量被假定为240%。列车的总重量是列车的自重与旅客的重量之和。相应地，由于旅客运量的变化而导致列车运行时的压重被任意的改变，从而影响到桥梁构件的应力作用范围。那概率性的旅客运量被考虑在载重模型中。图3(a)是旅客运量的柱式图解。图3(b)是概率分布由频率统计曲线图导出的。评估桥的剩余疲劳寿命的各种不同的程序现在也已被分别使用，它依靠荷载模型被分类开。

1)第1个方式为简单性程序：使用以乘客运量的柱式图解建立在以真正的数据上，来核算累积疲劳破坏。可容许的疲劳破坏从被给定的荷载作用周期的可容许的应力作用幅度中来评估。而且过去一直用此方式评估剩余疲劳寿命。

2)第2个方式为概率性程序。使用假定的建立在获得频率统计曲线和假定的概率模型的乘客运量的概率分布模型中，是疲劳破坏系数用来评估剩余疲劳寿命的用来预定可靠性水平。

3)第3个方式为确定性程序。使用载重模型。列车频繁的运行而最终导致材料的疲劳破坏。载重模型被从相等的旅客运量中获得，是平均值和标准偏差旅客运量分布的总和。在所有的那些程序中，旅行频率也被考虑在确定性的程序当中了。

自从铁路桥双车道交通系统开放之后，二列列车可能在相反的方向上(向南或向北)同时通过桥面的同一个位置，二列列车产生不同的应力作用时间和结果，每个重合的位置都会产生不同的应力作用范围。模拟这种巧合情况，巧合区域被划分为5个区间之内。因为列车有10个车厢，而且总长度接近200 m,考虑桥的部分有三跨桁架而且另外两个在两者的边上足有100 m的跨度，如图4所示。在车站交通时刻表中，列车在桥的两端被模拟的重合点。列车被假定为从每个测站开始，在30s之内或早或晚的比精确值。每列火车出发的时刻完全相同地也被统一地安排在假定的范围里。

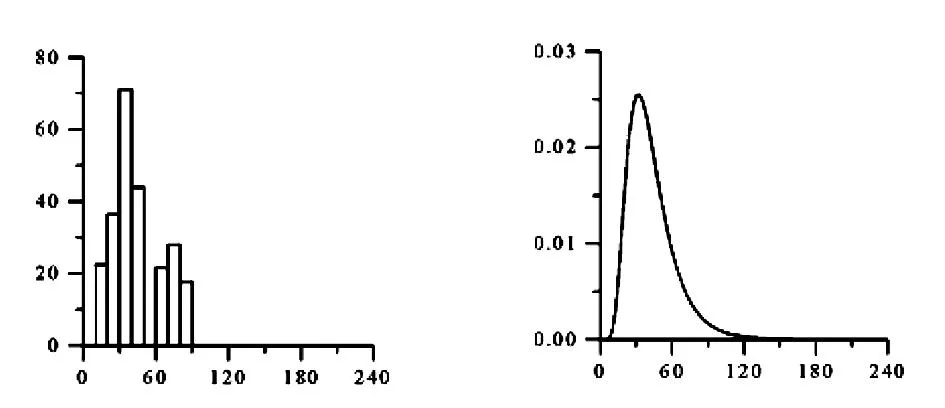
频率(数字)　 旅客运量(%)　 频率　乘客运量(%)

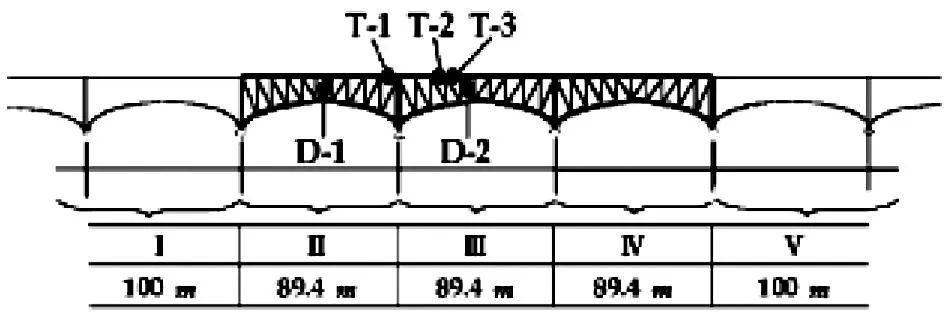
图4　列车在桥上的巧合区域

在单车道乘客的运量巧合情况通过给定的巧合位置与考虑的时间来确定用第一个与第二个方法。那时，在单车道交通里，乘客运量的重合情况通过考虑的时间和重合的位置及乘客平均运量来获得，评价乘客运量的重合区是一致的，因为两列车的重合大部分都发生在高峰时间内。第3种方式没有考虑列车相遇这种情况。

评估桥梁的剩余疲劳寿命，在分析中应该包含将来旅客运量和未来的交通量这样两种情况。假定交通运量同现在一样，只不过随着乘客的增加将会影响列车的载重量。在前一个时期，发现旅客运量以每年大约以4%的速率增加。然而随着新式交通系统的产生，将来列车的最大限度的容纳乘客的能力与将来乘客增长率将会减少。

3个不同的增量模型，例如线状、逐段线性、指数的模型都适用于将来乘客数目的增加见图5(a)。旅客运量的增量上限值为90%。因此可以通过将来达到旅客运量的分配方式来改变当前的旅客运量的分配方式，如图5(b)所示。通过对照概率性的程序，每个模型都要对比剩余疲劳寿命来评估。逐段线性模型主要用来分析所有的程序。

4动力试验和模拟检定分析

在三跨度连续平行弦桁架桥上的中间部位，动力试验已经被应用于此。分析的模拟结果在测量时已被校正。专业试验已经运用两种不同的类型试验去做：常态操作速率试验和各种不同的等速率测试。常态速率试验在白天期间被实行，特殊的，在高峰时刻要考虑最大的载重效果。在晚上，交通被关闭，空列车以预先指定的等速率运行在桥面上。从正常速率试验来看，以各种不同载重情况的历次作用次数上获得单车道交通与双车道交通有相同的巧合率。从等速率试验来看，动态的作用效果在运行速率中已经被证实。

结构分析以有限的元素模型来做指导。在相同的载重情况下，挑选应力作用次数大的构件。图6显示的是应力作用次数的例子，它通过专业计量和FE分析获得。数字模拟通过增加纠正的要素来检验。校正的要素通过动态专业测试的结果与FE分析的结果比较而获得。疲劳累积破坏(c)与最大限度应力幅度(△σ)通过列车的一个通道来检测决定要校正的要素。经发现，使用最大限度应力作用的范围能收益更多符合的结果比使用累积疲劳破坏的。应力幅度问题由正确的应力作用时间的频谱分析来做指导，这种方法已经被广为人知。

图5　乘客运量的增加模型

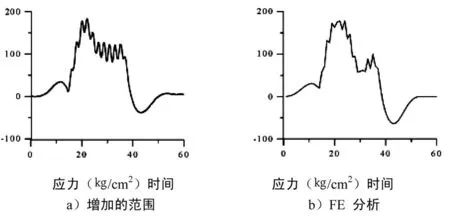
图6　应力作用的时间记录

参考文献：

[1]潘际炎.铁路桥梁设计中的疲劳可靠性理论[J].钢结构，1995(01)：1-8.

[作者简介]张薇(1982-)，女，内蒙古呼伦贝尔人，工程师。

[收稿日期]2015-04-24

中图分类号：U448.36

文献标识码：B

文章编号：1007-7596(2015)08-0074-03