多元优化算法可达性分析

李宝磊, 吕丹桔,2, 刘兰娟, 施心陵, 陈建华, 张榆锋

(1. 云南大学信息学院, 云南 昆明 650091;

2. 西南林业大学计算机与信息学院, 云南 昆明 650224)



多元优化算法可达性分析

李宝磊1, 吕丹桔1,2, 刘兰娟1, 施心陵1, 陈建华1, 张榆锋1

(1. 云南大学信息学院, 云南 昆明 650091;

2. 西南林业大学计算机与信息学院, 云南 昆明 650224)

摘要：提出了一种多元化群智能优化算法—多元优化算法。多元优化算法充分利用了现代计算机多核处理器,大内存的特点,通过多元化的搜索个体(元)对优化问题解空间进行搜索,并对历史信息进行选择记忆。该算法因搜索群具有分工不同的多元化特点而得名。搜索元按照职责不同而分为全局元和局部元,全局元负责在整个搜索空间进行全局搜索并找到潜在解区域,局部元负责在各个潜在解区间进行局部搜索以期望找到该区域更好的解。本文从理论上证明了该算法的可达性。基于标准函数的对比实验也验证了该方法在可达性方面优于其他几个参与比较的算法。

关键词：多元优化算法; 可达性; 全局元; 局部元

0引言

近几年计算机硬件技术突飞猛进,特别是多核处理器,大内存成了现代计算机的特点[1]。然而，目前经典的启发式群智能优化算法并没有充分利用现代计算机的硬件资源。本文基于计算机链表结构,提出了一种启发式、多元化群智能优化算法。

在众多的启发式群智能优化算法中,精英保留策略的基因(genetic algorithm with one elitist,EGA)算法[2]、自适应惯性权重的粒子群优化(particle swarm optimization with inertia weight,PSO -w)算法[3]以其操作简单,收敛速度快而被广泛应用在资源分配、道路规划、无线传感网络等实际问题中[4-6]。然而，它们受限于易陷入局部最优解而无法到达复杂多峰优化问题的全局最优解[7]。为了解决该问题,许多学者通过引入新策略以平衡全局和局部搜索能力来获得较好的全局到达性[8-9]。文献[10]通过引入了利用所有粒子历史最优信息更新粒子的策略提出来了全面学习粒子群优化(comprehensive learning particle swarm optimizer,CLPSO)算法。文献[11]提出来的萤火虫算法(firefly algorithm, FA)是受启发于萤火虫之间的相互吸引力与它们各自的亮度成正比及与它们的距离成反比。虽然这些算法在大部分优化问题中表现出良好的性能,但是它们都是从启发策略出发而没有考虑现代计算机运算的原理。也就是说,一方面，虽然大部分算法具有并行计算的能力,但是它们没有利用现代计算机具有多核处理器的特点。另一方面，这些算法为了减少算法的空间复杂度,抛弃了寻优过程中的历史信息,仅仅用了很少一部分内存,大部分内存空间是闲置的。实际上历史信息可以用于预测搜索结果以提高搜索效率[12]。

为了充分利用现代计算机的硬件资源并对优化问题的特点进行进一步的分析,本文提出了一种历史记忆,过程寻优的多元化优化算法。由于搜索元分工不同具有多元化的特点,因此把该算法命名为多元优化算法(multivariant optimization algorithm,MOA)。在本文提出的算法中,多个搜索元基于高效的信息共享机制按照各自的分工对解空间进行搜索以逼近全局最优解。搜索元按照分工不同可以分为全局搜索元和局部搜索元,全局搜索元在解空间中随机生成负责对全局进行搜索并对发现的潜在解区域进行记忆,局部搜索元在潜在解区域内进行局部搜索以找到该局部区域内的更优的解。搜索元利用结构表完成高效的信息筛选、记忆和共享以进行分工合作。

本文在第1节中描述了多元优化算法的基本思想以及具体实现。第2节对该算法的可达性进行了理论证明。第3节通过模拟实验从可达概率和可达精度两个方面比较了多元优化算法,精英保留策略的基因算法,自适应惯性权重的粒子群优化算法,全面学习粒子群优化算法,萤火虫算法的性能。实验结果表明,多元优化算法在可达性方面优于其他几个参与比较的算法。

1多元优化算法

多元优化算法的基本思想是对解空间进行交替的全局和局部搜索,通过对历史信息的筛选、记忆和共享来指导多元化搜索元分工合作对解空间进行全面和细致的探索。算法基于如图1所示的上三角型结构体对历史信息进行筛选、记忆和共享。结构体由一个全局有序链表和n个局部有序链表构成。全局链表长度为n,第i个局部链表长度为n-i+1。全局链表负责基于全局元的信息对全局潜在解区域的信息进行记忆,更新与共享。每个局部链表基于该局部内局部元的信息负责一个区域内历史信息的记忆与更新。

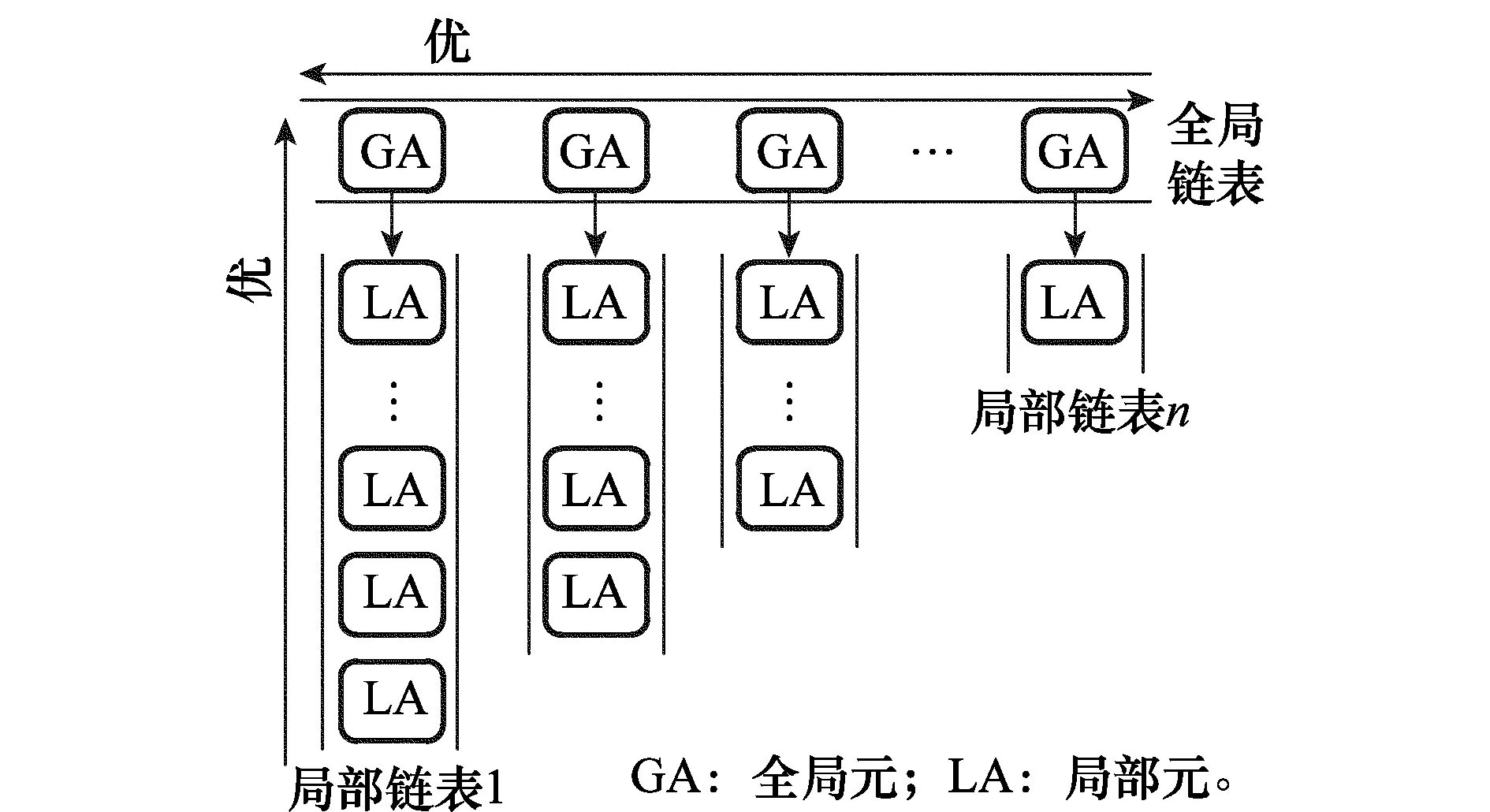
图1　上三角型结构体

图1算法中,本文以伪代码的形式详细描述了多元优化算法的实现过程。多元优化算法的一次迭代包括全局搜索和局部搜索两个阶段。在全局搜索阶段,根据式(1)在整个搜索空间中随机生成全局元GA实现对全局的搜索。

hi=unifrnd(mini,maxi)

(1)

式中,d是问题的维度;mini和maxi分别为解空间第i维的下界和上界;unifrnd(mini,maxi)函数返回一个均匀分布在mini和maxi之间的随机数。新生成的全局元与全局链表中的元比较,适应度值较好的全局元被作为潜在解区域的中心记录在结构体的全局链表中。在局部搜索阶段,根据式(2)在以全局元GA为中心,r为半径的局部邻域内随机生成局部元实现对各个潜在解区域的局部搜索。

(2)

式中,li(i=1,…,d)是-1~1之间的随机数。新生成的局部元与局部链表中的元比较,较好的元作为历史信息保留下来。如果局部元优于该区域的全局元,则该局部元将取代全局元作为新的潜在解区域中心进入全局链表。

由多元优化算法的实现可以看出:多元优化算法能够利用现代计算机多核处理器的特点,为每个局部链表分配一个处理核,多核处理器并行运算,各自负责一个局部链表的管理,实现局部搜索,信息共享和记忆。

多元优化算法如表1所示。

表1　多元优化算法

2多元优化算法可达性

可达性是指算法以概率1在有限次搜索后,搜索个体访问到全局最优解[13]。为了证明多元优化算法的可达性,首先描述了最小化优化问题,然后给出了解空间可达性和最优解可达性的定义,接着证明了多元优化算法具有可达性的充分条件,最后证明了多元优化算法满足可达性的充分条件,证明其具有可达性。

问题 1最小化优化问题。假设在给定有限非空集合S中,对于目标函数f:S→R存在最优解集合Ω={x*|x*∈S,f(x*)<ε},其中ε是可接受的目标函数值。优化问题亦即在解空间S中找到至少一个使目标函数最小化的点x*。

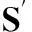
定理 1算法可达性。对于一个充分大的迭代次数N,优化算法具有可达性的充分条件为:

(3)

(4)

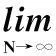
证毕

定理 2多元优化算法可达性。多元优化算法满足具有可达性的充分条件:

即多元优化算法具有可达性。

证明(1) 解空间可达性

其中,|Sk|表示集合Sk中元的个数。令

又因为SN⊆S,所以E|SN|≤|S|。综上可得

由于τ>0且S为有限非空解集合。当N足够大时,E|SN|=|S|。则E(|S|-|SN|)=0。由

可得

(2) 最优解可达性

令最优解不属于搜索过的解集合的概率为

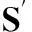
证毕

3仿真实验及结果分析

为了比较多元优化算法和其他8个常用启发式智能优化算法在可达性方面的性能。用200次独立测试统计得出的全局最优解到达率(accessibilityrate,AR)和可达精度作为评价指标。算法达到可接受的目标函数值ε时,认为该算法到达了全局最优解。根据式(5)计算n次迭代内的全局最优解到达率。

(5)

式中,Ar表示全局最优解到达率；xn是200次测试中,n次迭代内算法到达全局最优解的测试的个数;N为总测试次数。

本文用200次实验中获得的最小适应度值的均值来评价算法的可达精度。

3.1测试函数

参考文献本文从中选择了8个二维复杂测试函数。尽管这些函数都是低维的,但是由于其具有多峰性和欺骗性,大部分智能优化算法无法以100%的可达率找到这些函数的全局最优解。因此这些函数具有足够的复杂性来测试新方法[15-19]。测试函数及其全局最优解适应度值,可接受的目标函数值ε如下:

(1)Michalewicz[15]

搜索空间为:x1∈[0,5],x2∈[0,5];当d=2时,函数最小值为-1.801 3;可接受的目标函数值ε=-1.8。

(2) Langermann function[16]

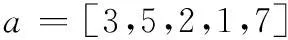
搜索空间为:x∈[0,10],y∈[0,10];函数最小值为-5.161 8;可接受的目标函数值ε=-5.16。

(3) Damavandi[17]

搜索空间为:x1∈[0,14],x2∈[0,14];函数最小值为0;可接受的目标函数值ε=1。

(4) YangStandingWave[18]

搜索空间为:x1∈[-20,20],x2∈[-20,20]函数最小值为-1;可接受的目标函数值ε=-0.99。

函数(5)~函数(8)是文献[19]中提出的新型十维合成多峰复杂测试函数。Suganthan教授在其个人主页上提供了这些函数的代码及其所使用的正交矩阵、偏移全局最优解、控制参数。这3个函数搜索空间为:xi∈[-5,5],i=1,…,10,最小值均为0。

(5) CF1

cf1~cf10: Sphere Function。

可接受的目标函数值ε=0.5。

(6) CF2

cf1~cf10: Griewank’s Function。

可接受的目标函数值ε=10。

(7) CF3

cf1~cf10: Griewank’s Function。

可接受的目标函数值ε=10。

(8) CF4

cf1~cf2: Ackley’s Function；

cf3~cf4: Rastrigin’s Function；

cf5~cf6: Weierstrass Function；

cf7~cf8: Griewank’s Function；

cf9~cf10: Sphere Function。

可接受的目标函数值ε=10。

3.2算法和参数设置

本文中所有的算法都是基于Matlab7.0实现的。所有算法的相同参数为:种群大小20,最大迭代次数500。

参与比较的算法以及文献中给出的它们最优参数如下:

(1)EGA算法:每次迭代种群更新率为0.8;交叉和变异的概率分别设置为0.2和0.01[2]。

(2)PSO-w算法: 惯性权重随着迭代次数的增加从1.4按照指数递减到0.5;加速常数c1和c2均为1.494 45[3]。

(3)CLPSO算法: 惯性权重随着迭代次数的增加从0.9按照指数递减到0.4;加速常数c为1.494 45;更新间隔为7[10]。

(4)FA算法:随机搜索因子α为0.2;吸引力参数β0为1;亮度吸收参数γ为1[11]。

(5)MOA算法: 结构体为三角形结构;求解二维和十维函数时队列长度分别为5和10;堆栈深度从左到右依次递减1,左边第一个堆栈栈深为10;全局搜索元个数与队列长度相等;局部搜索元组种群大小与其对应的堆栈深度相等;局部搜索半径r为0.1。

3.3实验结果分析

3.3.1到达率

图2给出了5种算法对8个复杂多峰函数寻优的到达率随迭代次数的曲线。

图2　到达率分析

由图2可以看出:

(1)MOA算法在解决除了CF2函数以外的优化问题中的到达率随着迭代次数的增加不断增加并超过其他算法。对于Michalewicz函数,除了FA算法,其他所有算法都能达到100%的到达率。然而对于其他7个测试函数,多数方法都以不同的概率陷入局部最优解而无法以100%的到达率到达全局最优解,特别是寻找Damavandi和CF4函数的最优值时。可见,尽管这些复杂函数具有容易把搜索个体引入局部最优解的特点,但是多元优化算法能够通过全局搜索跳出局部最优解发现全局最优解可能所在区域,然后通过局部搜索逐渐靠近全局最优解。

(2)MOA算法、CLPSO算法和FA算法在解决大部分优化问题时的到达率随着迭代次数的增加而增加。EGA算法和PSO-w算法的到达率达到一定值后不随着迭代次数的增加而增加,该现象在函数Langermann、CF1、CF2和CF3中较明显。可见MOA算法、CLPSO算法和FA算法具有跳出最优解的能力,迭代次数越多其到达全局最优解的概率就越大。而其他2种算法一旦陷入局部最优解,增加迭代次数不会对早熟收敛问题有所改善。

3.3.2可达精度

表2给出了5种算法对8个测试函数寻优的最小适应度值的均值以及标准差统计结果。数据格式为:均值±标准差,最好的结果用粗体标识。

表2　算法到达精度比较

从表2中可以得出以下结果:

(1) 对大部分函数寻优问题中,MOA算法获得最小的适应度值均值。这说明:EGA、PSO -w、CLPSO和FA算法容易陷入这些复杂多峰测试函数局部最优解而无法保证较好的到达精度。然而,MOA算法能够以较高的到达精度找到全局最优解。可见,MOA算法在可达精度方面优于EGA算法、PSO -w算法、FA算法,CLPSO算法。

(2) 全面学习粒子群优化算法和萤火虫算法获得的适应硬度值均值小于传统的EGA算法和PSO -w算法。这说明与CLPSO、FA算法相比,EGA、PSO -w算法更容易陷入局部最优解,而无法获得较高的到达精度。

4结论

本文提出了一种充分利用计算机多核、大内存特点的多元化优化算法。多元优化算法中,多元化搜索元分工协作分别对解空间进行全局和局部搜索,而不必考虑均衡全局搜索和局部搜索的问题,这保证了算法能够以一定的可达精度到达全局最优解。本文从理论上证明了该方法的可达性,仿真实验也验证了该方法在到达率和可达精度方面优于其他几个经典的启发式群智能优化算法。该算法在复杂优化问题中具有较好的可达性,对于解决容易导致算法早熟收敛的全局优化问题具有良好的表现。

本文主要集中在从理论和实验两个方面证明MOA算法的可达性。进一步的工作将集中在通过利用结构体中的历史搜索信息预测搜索结果以保证可达性的前提下减少适应度值函数评价次数,从而提高搜索效率。

[1] Wu J, Tang C J, Li T Y, et al. Parallel gene expression programming based on general multi-core processor[J].ComputerScience, 2012, 38(11): 296-302.(吴江, 唐常杰, 李太勇, 等. 基于通用多核处理器平台的并行基因表达式编程算法[J].计算机科学, 2012, 38(11): 296-302.)

[2] Djurisic A B. Elite genetic algorithms with adaptive mutations for solving continuous optimization problems-application to modeling of the optical constants of solids[J].OpticsCommunications, 1998, 151(1): 147-159.

[3] Shi Y, Eberhart R C. A modified particle swarm optimizer[C]∥Proc.oftheIEEEWorldCongressonComputationalIntelligence, 1998: 69-73.

[4] Gao S, Yang J Y. Solving weapon-target assignment problems by particle swarm optimization algorithm[J].SystemsEngineeringandElectronics, 2005, 27(7): 1250-1252.(高尚, 杨静宇. 武器-目标分配问题的粒子群优化算法[J].系统工程与电子技术, 2005, 27(7): 1250-1252.)

[5] Wang L F, Song J S, Wang Z Y, et al. Vehicle routing optimization with hard time windows in battlefield resources distribution[J].SystemsEngineeringandElectronics, 2013, 35(4): 770-776.(王连锋, 宋建社, 王正元, 等. 带硬时间窗的战场物资配送车辆路径优化[J].系统工程与电子技术, 2013, 35(4): 770-776.)

[6] Kulkarni R V, Venayagamoorthy G K. Particle swarm optimization in wireless-sensor networks: a brief survey[J].IEEETrans.onSystems,Man,andCybernetics,PartC:ApplicationsandReviews, 2011, 41(2): 262-267.

[7] Bi X J, Wang Y J. Niche artificial bee colony algorithm for multi-peak function optimization[J].SystemsEngineeringandElectronics, 2011, 33(11): 2564-2568.(毕晓君, 王艳娇. 用于多峰函数优化的小生境人工蜂群算法[J].系统工程与电子技术, 2011, 33(11): 2564-2568.)

[8] Chen Y L, Zhang P L, Li S, et al. Adaptive niche quantum evolutionary algorithm for multimodal function[J].SystemsEngineeringandElectronics,2014,36(2):403-408.(陈彦龙,张培林,李胜,等.面向多峰函数的自适应小生境量子进化算法[J].系统工程与电子技术,2014,36(2):403-408.)

[10] Liang J J, Qin A K, Suganthan P N. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J].IEEETrans.onEvolutionaryComputation,2006,10(3):281-295.

[11] Yang X S. Firefly algorithm, stochastic test functions and design optimisation, international[J].JournalofBio-InspiredComputation, 2010, 2(2): 78-84.

[12] Zhang Y, Su G S, Yan L B. Cooperative optimization algorithm based on particle swarm optimization and Gaussian process[J].SystemsEngineeringandElectronics, 2013, 35(6): 1342-1347.(张研, 苏国韶, 燕柳斌. 基于粒子群优化与高斯过程的协同优化算法[J].系统工程与电子技术, 2013, 35(6): 1342-1347.)

[13] Li M Q, Kou J S, Lin D, et al.Thebasictheoryandapplicationgeneticalgorithm[M]. Beijing: Science Press, 2002: 78-79.(李敏强,寇纪淞,林丹,等.遗传算法的基本理论与应用[M].北京:科学出版社,2002:78-79.)

[14] Zhang J Y, Xu J, Bao Z. Attainability of genetic crossover operator[J].ActaAutomaticaSinica, 2002, 28(1): 120-125.(张军英,许进,保铮.遗传交叉运算的可达性研究[J].自动化学报,2002,28(1):120-125.)

[15] Bingham D. Virtual library of simulation experiments: test functions and datasets[EB/OL].[2014-05-25].http:∥www.sfu.ca/~ssurjano/michal. html.

[16] Bersini H, Dorigo M, Langerman S. Results of the first international contest on evolutionary optimization[C]∥Proc.oftheIEEEInternationalConferenceonEvolutionaryComputation, 1996: 611-615.

[17] Damavandi N, Safavi-Naeini S. A hybrid evolutionary programming method for circuit optimization[J].IEEETrans.onCircuitsandSystemsI:RegularPapers,2005,52(5):902-910.

[18] Yang X S.Engineeringoptimization:anintroductionwithmetaheuristicapplications[M].New Jersey:Wiley,2010:265-265.

[19] Liang J J, Suganthan P N, Deb K. Novel composition test functions for numerical global optimization[C]∥Proc.oftheIEEESwarmIntelligenceSymposium,2005: 68-75.

李宝磊(1987-),男,博士研究生,主要研究方向为智能优化算法、信号处理。

E-mail:bl_li@qq.com

吕丹桔(1977-),女,博士研究生,主要研究方向为智能优化算法、信号检测。

E-mail:lvdanjv@gmail.com

刘兰娟(1989-),女,硕士研究生,主要研究方向为智能优化算法、离散优化。

E-mail:363209350@qq.com

施心陵(1956-),男,教授,主要研究方向为自适应信号处理、智能优化算法。

E-mail:xlshi@ynu.edu.cn

陈建华(1964-),男,教授,博士,主要研究方向为压缩编码、图像处理。

E-mail:chenjh@ynu.edu.cn

张榆锋(1965-),男,教授,博士,主要研究方向为医学信号处理、超声检测。

E-mail:zhangyf@ynu.edu.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20150120.1050.002.html

On accessibility of multivariant optimization algorithm

LI Bao-lei1, LÜ Dan-ju1,2, LIU Lan-juan1, SHI Xin-ling1, CHEN Jian-hua1, ZHANG Yu-feng1

(1.SchoolofInformationEngineering,YunnanUniversity,Kunming650091,China;

2.SchoolofComputerandInformation,SouthwestForestryUniversity,Kunming650224,China)

Abstract:A multivariant optimization algorithm (MOA) is proposed. The proposed method makes full use of the multi-core processors and the large memory of modern computers. Multivariant searchers (atoms) explore the solution space and remember the historical information selectively. The MOA gets its name from the multivariant characters of multiple searchers. Atoms are divided into global atoms and local atoms according to variant responsibilities. Global atoms explore the whole solution space to discover potential areas. Local atoms exploit potential areas for a local refinement. Theoretically, the MOA is proved to be accessible to the global optimal solution. Experiments based on benchmark functions show that the MOA has competitive performance compared with other methods in terms of accessibility.

Keywords:multivariant optimization algorithm (MOA); accessibility; global atoms; local atoms

作者简介：

中图分类号：TP 18

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2015.07.31

基金项目：国家自然科学基金(61361010)；云南省自然科学基金重点项目(2013FA008)资助课题

收稿日期：2014-06-03；修回日期：2014-10-08；网络优先出版日期：2015-01-20。